数列·双基能力训练

数列·双基能力训练

　

(一)选择题：

1．数列{a_n}的通项公式是a_n=n²-3n-28，这个数从第几项起各项都是正数　[　　]．

A．第6项　 B．第7项　 C．第8项　 D．第9项

2．数列1，3，6，10，…的一个通项公式a_n=　　　　　　　　　　　　　　  [　　]．

A．n²-n＋1

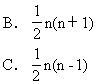
D．2ⁿ⁺¹-3

3．数列7，9，11，…，2n-1的项数是　　　　　　　　　　　　　　　　　　　  [　　]

A．n

B．n-1

C．n-2

D．n-3

A．18项

B．19项

C．17项

D．20项

5．无穷数列1，2³，2⁶，2⁹，…，2³ⁿ⁺⁶，…中，2³ⁿ⁺⁶是第　　　　　　　　  [　　]．

A．3n＋6项

B．3n＋7项

C．n＋2项

D．n＋3项

6．一个数列{a_n}，其中a₁=3，a₂=6，a_n+2=a_n+1-a_n，那么这个数列的第5项是　　  [　　]

A．-6　　　　　　　　　　　  B．-3

C．6　　　　　　　　　　　　  D．3

7．在数列1，1，2，3，5，8，13，x，34，55，…中，x的值是 [　　]．

A．19　　　　　　　　　　　  B．20

C．21　　　　　　　　　　　  D．22

(二)填空题：

8．写出下列各数列的通项公式：

(1)3，8，15，24，35，…　a_n=______；

(3)3，33，333，3333，33333，…　a_n=_______；

(4)3，5，3，5，3，…　a_n=_______．

9．数列{a_n}的通项公式为a_n=log_n＋1(n＋2)，则它的前14项的积为_________．

10．已知数列{a_n}中，a₁=2，a_n=a_n-1-2，则a₃=______，a₆=_____．

11．数列{a_n}为3，5，7，…，2n＋1，…，数列{b_n}中，b₁=a₁，当n≥2时b_n＝ab_n-1，则b₄=______，b₅=______．

12．数列{a_n}中，a₁=1，a_n＋1=f(a_n)，且f(x)=x²-1，写出这个数列的前5项______．

13．已知数列{a_n}的前n项和为S_n=3＋2ⁿ，则通项a_n=______．

14．在数列{a_n}中，已知S_n=2n³-3n，那么a₆＋a₇=______．

______项．

(三)解答题：

(1)写出数列的前5项；

(2)猜想数列的通项公式．

200，380三个数中，哪个数是数列{a_n}中的项，是第几项？

任意大于1的自然数n，都有2a_n+a_n-1=0，S_n-1＋2S_n=-6成立

数列·双基能力训练·答案提示

　

(一)1．C　　　　　　  2．B　　　　　　 3．D　　　　　　  4．B

5．D　　　　　　 6．A　　　　　　 7．C

提示：

7．此数列的递推公式是a₁=1，a₂=1，a_n+1=a_n＋a_n-1，则x=8＋13=21，

故选C．

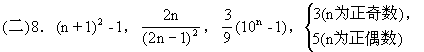
9．4　　　　　　  10．-2，-8　　　　　　　　  11．31，63

12．1，0，-1，0，-1

13．5(n-1),2n-1(n≥2)

14．430　　　　　　　　　 15．8

提示：

9．由a_n=log_n+1(n＋2)，则a₁·a₂·a₃……a₁₄=log₂3×log₃4×log₄5×…×log₁₅16=log₂16=4．

11．数列{a_n}的通项公式为a_n=2n＋1．

当n≥2时，b₂=ab₁=aa₁=a₃=7，

b₃=ab₂=a₇=2×7×1=15，

b₄=ab₃=a₁₅=2×15＋1=31，

b₅=ab₄=a₃₁=2×31+1=63．

12．a_n＋1=a_n²-1．a₁=1，则a₂=a₁²-1=0，a₃=a₂²-1=-1，a₄=a₃²-1=(-1)²-1=0，a₅=a₄²-1=-1．

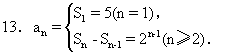
14．a₆＋a₇=S₇-S₅=2×7³-3×7-2×5³＋3×5=430．

(三)

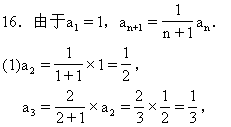
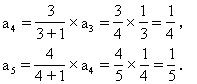
当n=1时，a₁=S₁=2，

当n≥2时，a_n=S_n-S_n-1=n(n＋1)．

因为a₁符合n≥2时a_n的解析式，所以数列{a_n}的通项公式为

a_n=n(n＋1)．

经检验a₁₁=132，a₁₉=380，而200不是该数列中的项．

18．证明:

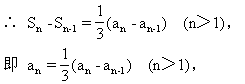
∴　2a_n＋a_n-1=0(n＞1)．

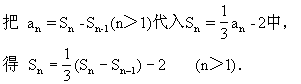
可化简为　S_n-1＋2S_n=-6　　(n＞1)