西安中学2000-2001学年度第一学期期中考试
高一年级数学试题
命题人：崔建宜
一、选择题（每小题只有一个答案正确。每小题3分，共36分）
1、给出下面六个关系式：①
；②
；③
④
; ⑤
; ⑥
。正确的为（ ）
A、①④B、②④⑤⑥C、①⑤⑥D、③④⑤
2、下列命题：①三点确定一个平面；②两条直线可以确定一个平面；③不同在任何一个平面内的两条直线叫异面直线；④如果一个角的两边和另一个角的两边分别平行，那么这两个角相等；⑤两条异面直线所成角范围为[0°，90°]。以上正确个数为（ ）
A、0 B、1C、2 D、3
3、M={xx-1≤1}，
，则M∪N=（ ）
A、[0，1） B、（1，2]
C、（-1，2] D、（-∞，-1）∪[0，+∞）
4、在从集合A到集合B的映射中，下列说法不正确的是（ ）
A、A中每一个元素在B中都有像
B、A中不同元素在B中的像必不相同
C、B中某一元素在A中的原像可能不止一个
D、B中元素在A中可以没有原像
5、函数
，x∈[0，3]，则该函数值域（ ）
A、R B、（-∞，2）C、[-2，1] D、[-2，2]
6、下列命题：
①若直线
平面M，直线
，且a∩b=φ，则a∥M
②直线a∥直线b，
平面M，则a∥M
③直线a垂直于平面M内的无数条直线，则a⊥M
④若直线a∥平面M，直线a⊥直线b，则b⊥M
其中正确的命题个数是（ ）
A、0，B、1 C、2 D、3
7、
在（-∞，2]上是减函数，则m取值范围（ ）
A、m=8 B、m≤8 C、m≥8 D、不能确定
8、下列函数中在（-∞，0）上单调递减的是（ ）
A、
B、
C、y=2x+1 D、
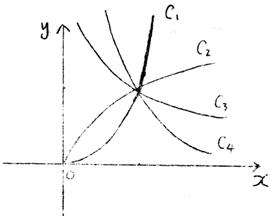
9、图中曲线是幂函数
在第一象限的图像，已知n取±2、
，则相应曲线
、
、
、
的n依次为（ ）
A、-2，
，
，2
B、2，，，-2
C、，-2，2，
D、2，，-2，
10、在下列函数中：①
；②
；
③y=x-1；④y=x+1-x-1。其中非奇非偶的函数是（ ）
A、①④B、③④C、①③④D、①③
11、已知异面直线a,b分别在平面α，β内，且α∩β=c，则直线c（ ）
A、将同时与a,b相交 B、至少与a,b中一条相交
C、至多与a,b中一条相交 D、至少与a,b中一条平行
12、下列命题：①函数是定义域到值域的映射；②
在其定义域内为减函数；③和两条异面直线都相交的两条直线为异面直线；④和两条异面直线都垂直的直线叫两异面直线的公垂线。以上错误的命题个数（ ）
A、0 B、1 C、2 D、3
二、填空题（每小题3分，共12分）
13、函数
定义域______。
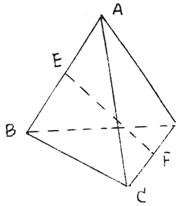
14、如图，在空间四边形ABCD中，AD=BC=2， E、F分别是AB、CD中点，若
，则AD与BC所成角的余弦为________。
15、奇函数f(x)定义域为
，且在[0，+∞]上递增，那么f(-2)、f(-1)、f(1)由小到大顺序________。
16、若函数
，定义域为R，则实数k的取值范围________。
三、解答题（应写出解答或证明过程）
17、（8分）已知
，B={xx-a<0}。
①若A∩B=φ，求a取值范围。
②若
，求a取值范围。
18、（12分）叙述并证明直线与平面平行的判定定理。
19、（10分）证明：
在（0，2]上为减函数。
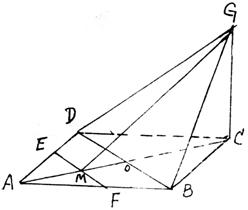
20、（12分）已知E、F分别为正方形ABCD边AD、AB的中点，E交AC于M，GC垂直于平面ABCD。
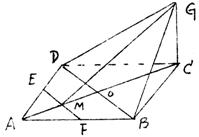
求证：
①EF∥平面GBD
②EF⊥平面GMC
21、（10分）某商店在最近的30天内的价格f(t)与时间t（单位：天的函数关系是
f(t)=t+10(0<t≤30，t∈N)，日销售量g(t)是时间t的函数关系g(t)=-t+35（0<t≤30，t∈N）。求这种商品的日销售额的最大值。
西安中学2000-2001学年度第一学期期中考试
高一数学试题答案
一、选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| B | B | C | B | D | A | B | A | B | D | B | D |
二、填空题：13、{xx>5或x≤-3且x≠-1}或（-∞，-11）∪（-11，-3]∪（5，+∞）
14、 15、f(-2)<f(-1)<f(1) 16、
三、解答题：
17、解∵
∴-2<x<4
∴A=（-2，4）B=（-∞，a）
（1）若A∩B=φ，则a≤-2
(2)若
则a≥4
18、判定定理：如果平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行。
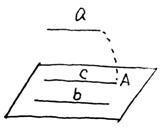
已知：
，
，a∥b
求证：a∥α
证明：∵
∴a∥α或a∩α=A
假设a∩α=A,∵a∥b∴
在平面α内过点A作直线c∥b，由公理4知a∥c，这与a∩c=A矛盾，∴a∥α
19、证明：设
∵
∴
∴
∴
∴f(x)在（0，2]上为减函数。
20、证明（1）∵E、F分别为AD，AB中点
∴EF∥BD。
又
平面BDG， 
面BDG
∴EF∥平面BDG。
（2）∵GC⊥平面ABCD
平面ABCD
∴GC⊥EF
又ABCD为正方形∴BD⊥AC
而EF∥BD ∴EF⊥AC
∵AC， 
平面GMC， 且AC∩GC=C
∴EF⊥平面GCM
21、设日销售额为y
则y=f(t)·g(t)
=（t+10）(-t+35)
(0<t≤30，t∈N)
由于0<t≤30，t∈N
∴t=12或13时 
答：第12天或第13天的日销售额最大最大值为506。