2001学年度第二学期期中考试
高一数学试题 命题人:王宁岚 2002.4
一、选择题:(![]() )
)
1、下列命题正确的是:
A、第一象限角都是锐角 B、终边相同的角相等
C、第二象限角比第一象限角大 D、钝角是第二象限角
2、若角![]() 是第二象限角,则角
是第二象限角,则角![]() 是:
是:
A、第一象限角 B、第一或第二象限角
C、第一或第三象限角 D、第一或第四象限角
3、函数![]() 的图象的一条对称轴是:
的图象的一条对称轴是:
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
*4、已知函数![]() (
(![]() <
<![]() )的图象的一部分如图所示,则:
)的图象的一部分如图所示,则:
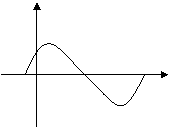 A、
A、![]()
![]() ,
,![]()
![]() B、
B、![]()
![]() ,
,![]()
![]()
C、![]() 2,
2,![]()
![]() D、
D、![]() 2,
2,![]()
![]()
5、![]() ,且
,且![]() <
<![]() <
<![]() ,则
,则![]() 的值为:
的值为:
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
*6、如果x,y![]() (0,
(0,![]() ),且tanx<coty,那么:
),且tanx<coty,那么:
A、x+y>![]() B、x+y<
B、x+y<![]() C、x>y D、x<y
C、x>y D、x<y
7、函数![]() 在一个周期内的图象是:
在一个周期内的图象是:
![]()
![]()
![]()
![]()
![]()
![]()
A B
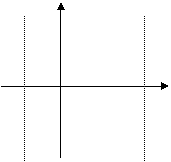 | 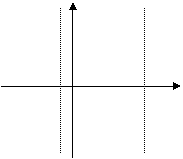 | ||
C D
*8、化简![]() 的结果是:
的结果是:
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、已知![]() 和
和![]() 是方程
是方程![]() 的两根,则
的两根,则![]() 、
、![]() 间的关系是:
间的关系是:
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、已知![]() ,
,![]() (0,2
(0,2![]() ),则角
),则角![]() 等于:
等于:
A、![]() B、
B、![]()
C、![]() D、
D、![]()
11、要得到![]() 的图象,只要将函数
的图象,只要将函数![]() 的图象:
的图象:
A、向左平移![]() B、向右平移
B、向右平移![]()
C、向左平移![]() D、向右平移
D、向右平移![]()
12、函数![]() 的单调递减区间:
的单调递减区间:
A、[![]() ,
,![]() ]
]![]() B、[
B、[![]() ,
,![]() ]
]![]()
C、[![]() ,
,![]() ]
]![]() D、[
D、[![]() ,
,![]() ]
]![]()
二、填空题(![]() )
)
13、函数![]() 的振幅为_________,周期为_________,相位为_________,初相为__________。
的振幅为_________,周期为_________,相位为_________,初相为__________。
*14、已知![]() ,则
,则![]() =___________。
=___________。
15、函数![]() 的定义域为____________________,值域为__________________。
的定义域为____________________,值域为__________________。
*16、购买一件售价为6万元的商品,首期付款4万元,余额采用分期付款(一年内付清),已知月利率0.8%,每二个月付一次,分六次付清,则每次付款为_____________元。
三、解答题
17、求值:[![]() ]
]![]()
18、已知![]() ,
,![]() ,并且
,并且![]() ,
,![]() 均为锐角,求
均为锐角,求![]()
19、已知![]() ,
,![]() ,且
,且![]() <
<![]() <
<![]() ,
,![]() <
<![]() <
<![]() ,求
,求![]() 的值。
的值。
20、用“五点法”作![]() 的图象,并说明图象可由函数
的图象,并说明图象可由函数![]() 的图象经过怎样的变换得到。
的图象经过怎样的变换得到。
21、已知函数f(x)=![]()
⑴求函数f(x)的最小正周期。
⑵求函数f(x)的最大值及取最大值时的x值。
⑶求函数f(x)的单调递增区间。
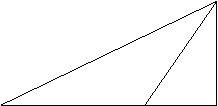
22、一条河宽1千米,相距4千米(直线距离)的两座城市A与B分别位于河的两岸,现需铺设电缆,连通A与B,已知铺地下电缆的修建费为2万元/千米,假定两岸是平行直线,问:如何确定M,其中AM与AD的夹角为![]() ,使铺水下电缆AM和铺地下电缆的BM的总费用最小?(精确到0.1万元)
,使铺水下电缆AM和铺地下电缆的BM的总费用最小?(精确到0.1万元)
 |
新昌中学2001学年度第二学期期中考试
高一数学答题卷 2002.4
| 总分 | 复核人 | 总得分 | ||
| 加分人 | 卷面分 |
| 得分 | |
| 评卷人 |
一、选择题:(![]() )
)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 得分 | |
| 评卷人 |
二、填空题:(![]() )
)
13、_________ __________ __________ __________
14、______________
15、___________________ ____________________
16、______________
| 得分 | |
| 评卷人 |
三、解答题
17、解:
| 得分 | |
| 评卷人 |
18、解:
| 得分 | |
| 评卷人 |
19、解:
| 得分 | |
| 评卷人 |
20、解:
| 得分 | |
| 评卷人 |
21、解:
| 得分 | |
| 评卷人 |
22、解: