高中代数上册复习训练题
一. 选择题
1. 设集合
，从M到P的映射
满足
，那么不同映射的个数是（ ）
A. 7 B. 6 C. 4 D. 2
2. 下列判断中正确的是（ ）
A. 
是偶函数
B. 
是奇函数
C. 
既是奇函数又是偶函数
D. 
是非奇非偶函数
3. 函数
与函数
的图象（ ）
A. 关于直线
对称 B. 关于直线
对称
C. 关于直线
对称 D. 关于直线
对称
4. 函数
的图象与
轴围成的封闭图形的面积是（ ）
A. 2 B. 
C.
1 D. 
5. 
是“函数
在
上恒有
”的（ ）
A. 充分非必要条件 B. 必要非充分条件
C. 充分必要条件 D. 非必要非充分条件
6. 在区间（
）上是增函数的是（ ）
A. 
B. 
C. 
D. 
7. 给出如下的四个函数方程和四个函数图象：
（1）
（2）
（3）
（4）
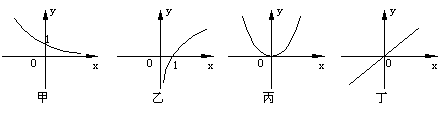
它们之间对应关系都正确的一组是（ ）
A. 甲—（3），乙—（1），丙—（2），丁—（4）
B. 甲—（1），乙—（2），丙—（3），丁—（4）
C. 甲—（2），乙—（4），丙—（1），丁—（3）
D. 甲—（2），乙—（3），丙—（4），丁—（1）
8. 已知
是偶函数，且当
时，
为减函数，又记
，则有（ ）
A. 
B. 
C. 
D. 
9. 将进货单价为40元的商品按50元一个销售时，能售出500个；如果这种商品每个提价1元，销售量就减少10个，为了获得最大利润，每个售价应定为（ ）
A. 45元 B. 50元 C. 60元 D. 70元
10. 角
终边上有一点
，那么角等于（以下
）（ ）
A. 
B. 
C. 
D. 
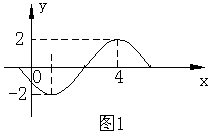
11. 如果函数
的一段图象如图1，那么函数表达式是（ ）
A. 
B. 
C. 
D. 
12. 要得到函数
的图象，只要将函数
的图象（ ）
A. 向右平移
个单位 B. 向左平移个单位
C. 向右平移
个单位 D. 向左平移个单位
13. 下列命题中，正确的是（ ）
A. 若
，则
B. 函数
的最小正周期是
C. 在
中，若
，那么是等腰直角三角形
D. 将函数
的图象上点的横坐标变为原来的倍，然后向左平移，可得到函数
的图象
14. 函数
的最小正周期是2，且图象关于直线
对称，那么
的一个值可以是（ ）
A. 
B. 
C. 
D.
15. 设函数
的最大值为，最小值为
，那么
的值为（ )
A. 
B. 
C.
0 D. 
二. 填空题
16. 已知
，则实数
的取值范围是__________。
17. 如果
是奇函数，那么
__________
18. 设函数的定义域是Ｒ，且满足条件，
，那么
__________。
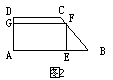
19. 在如图2的直角梯形ＡＢＣＤ中，
，下底ＡＢ＝6，上底ＣＤ＝4，高ＡＤ＝2，那么它的内接矩形ＡＥＦＧ的最大面积是__________。
20. 在中，给出下列命题：
（1）是锐角三角形
（2）
（3）
（4）
其中正确命题的序号是__________。
三. 解答题：
21. 设
，若当
时，有意义，求实数的取值范围。
22. 已知
，且
，求
的值。
23. 已知
，
。
（1）求的表达式；
（2）判断函数的奇偶性和单调性；
（3）若当
时，有
成立，求实数的取值范围。
24. 设
。
（1）求的定义域和值域；
（2）求的反函数
；
（3）实数
取何值时，关于的方程
在区间
上有相异的实根，并求此时两根之和。
25. 设函数
，又函数
的图象与
的图象关于直线对称。
（1）求函数的解析式；
（2）设
和
是
的定义域内任意两个值，且
，求证
；
（3）设A、B是图象上的任意不同的两点，证明直线AB必与直线相交。
26. 设
的最大值是3，求
的值。
27. 在中，记条件
，条件
。判断条件
是条件
的充分条件，还是必要条件，并证明你的结论。
28. 已知二次函数
（
为常数，且
）满足条件：
，且方程
有等根。
（1）求的解析式；
（2）是否存在实数
，使的定义域为
，值域为
？如果存在，求出
的值；如果不存在，说明理由。
参考答案
一. ABCDB DDADD CADAA
二. 16. 
17. 0 18. 1
19. 8 20. （1）（2）（3）
三. 21. 应有
，即知
对恒成立。而右端的函数是增函数，当
时，它取得最大值是
，从而的取值范围是
。
22. 原式
将已知式平方，求得
。
又由，知
而
，
则
，
从而原式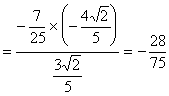
23. （1）设
，得
，代入题设，从而可求得
。
（2）计算得
，故是奇函数。
当
时，
是增函数，又
，从而是增函数，当
时，是减函数，又
，从而也是增函数。
综上，当时，总是增函数。
（3）由题设及是奇函数、增函数，有
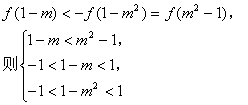
求出
24. （1）定义域是
，值域是
。
（2）
（3）方程即
设
，由
，有
，即
在
内有相异两实根，记
，则
解得
又
，则
，
从而
。
25. （1）知
互为反函数，可求得
。
（2）设
，则
（3）设
和
是图象上不同的两点，由（2）知
可见
，而直线的斜率为1，故直线AB必与直线相交。
26. 
。
（1）若
，
则当
时，有最大值。
由最大值
求得
（2）若
，则当
时，有最大值。
由最大值
求得
综上可知
27. 由条件
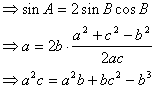
若
，则
可见总能推得
，即
。
反之，设成立，即有，来推得，则只要证明
，可先证
（*）
只要证
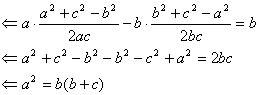
由条件，知上式成立，故（*）成立，即有，而由，知
，即
，因此必有，即
，可见
。
综上可知，
的充要条件。
28. （1）依题意，
有等根，故
，得
。
由
，得
恒成立，即
恒成立。故有
且
，得
。
所以
（2）假设存在满足条件的
，因为
，
所以
。
而抛物线的对称轴是，故
时，在上为增函数，则有
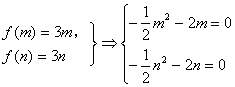
求得
又
，故
所以存在实数，使的定义域为
，值域为
。