高一数学数列复习题

数列复习题

 班级______　　姓名______　　学号_______

一、选择题　　　　

1、若数列{a_n}的通项公式是a_n=2(n＋1)＋3，则此数列　　(　　)

(A)是公差为2的等差数列　　　　　　　　 (B)是公差为3的等差数列

(C) 是公差为5的等差数列　　　　　　　  (D)不是等差数列

2、等差数列{a_n}中，a₁=3,a₁₀₀=36,则a₃＋a₉₈等于　　　  (　　)

(A)36　　　　　　 (B)38　　　　　　 (C)39　　　　　　　 (D)42

3、含2n+1个项的等差数列，其奇数项的和与偶数项的和之比为　 (　　)

(A)　　　　 (B)　　　　 (C)　　　　(D)

4、设等差数列的首项为a,公差为d，则它含负数项且只有有限个负数项的条件是　　　　　　 　　　 (　　)

(A)a＞0,d＞0 　　 (B)a＞0,d＜0　　　(C)a＜0,d＞0 　　 (D)a＜0,d＜0

5、在等差数列{a_n}中，公差为d，已知S₁₀＝4S₅，则是　　　　　 (　　)

(A)　　　　　　  (B)2　　　　　　　 (C)　　　　　　　  (D)4

6、设{a_n}是公差为－2的等差数列，如果a₁+ a₄+ a₇+……+ a₉₇=50，则a₃+ a₆+ a₉……+ a₉₉=　　　　　　　　　  (　　)

(A)182　　　　　  (B)－80　　　　　　  (C)－82　　　　　　 (D)－84

7、等差数列{a_n} 中，S₁₅=90，则a₈=　　　　　　　　　 (　　)

(A)3　　　　　　　  (B)4　　　　　　　 (C)6　　　　　　　  (D)12

8、等差数列{a_n}中，前三项依次为，则a₁₀₁=　　　　　 (　　)

(A)　　　　　　 (B)　　　　　　  (C)24　　　　　　 (D)

9、数列{a_n}的通项公式，已知它的前n项和为S_n=9，则项数n=　　　　　　　　　　　　 (　　)

(A)9　　　　　　 (B)10　　　　　　  (C)99　　　　　　 (D)100

10、等差数列{a_n}中，a₃+ a₄+ a₅+ a₆+ a₇=450，求a₂+a₈=　　 (　　)

(A)45　　　　　　　 (B)75　　　　　　　 (C)180　　　　　　  (D)300

11、已知{a_n}是等差数列，且a₂+ a₃+ a₈+ a₁₁=48，则a₆+ a₇=　　　　(　　)

(A)12　　　　　　 (B)16　　　　　　 (C)20　　　　　　　　 (D)24

12、在项数为2n+1的等差数列中，若所有奇数项的和为165，所有偶数项的和为150，则n等于　　　　　　　　　　　　　　　　 (　　)

(A)9　　　　　　 (B)10　　　　　　 (C)11　　　　　  (D)12

13、等差数列{a_n} 的前m项和为30，前2m项和为100，则它的前3m项和为(　　)

(A)130　　　　　  (B)170　　　　　　  (C)210　　　　　　 (D)160

14、等差数列{a_n}的公差为，且S₁₀₀=145，则奇数项的和a₁+a₃+a₅+……+ a₉₉=(　　)

(A)60　　　　　  (B)80　　　　　　 (C)72.5　　　　　　 (D)其它的值

15、等差数列{a_n}中，a₁+a₂+……a₁₀=15，a₁₁+a₁₂+……a₂₀=20，则a₂₁+a₂₂+……a₃₀=(　  )

(A)15　　　　　　 (B)25　　　　　　  (C)35　　　　　　　 (D)45

16、等差数列{a_n}中，a₁=3，a₁₀₀=36，则a₃+a₉₈=　　　　　　　　　　　　 (　　)

(A)36　　　　　　  (B)39　　　　　　 (C)42　　　　　　  (D)45

17、{a_n}是公差为2的等差数列，a₁+a₄+a₇+……+a₉₇=50，则a₃+a₆+……+ a₉₉= (　　)

(A)－50　　　　　　 (B)50　　　　　　  (C)16　　　　　　  (D)1.82

18、若等差数列{a_n}中，S₁₇=102，则a₉=　　　　　　　　  (　　)

(A)3　　　　　　  (B)4　　　　　　  (C)5　　　　　　　 (D)6

19、

夏季高山上温度从山脚起每升高100米，降低0.7℃，已知山顶的温度是14.1℃，山脚的温度是26℃，则山的相对高度是　　　　　　　　　　　　  (　　)

(A)1500　　　　　 (B)1600　　　　　　 (C)1700　　　　　  (D)1800

20、若x≠y，且两个数列：x，a₁，a₂，y 和x，b₁，b₂，b₃，y各成等差数列，那么　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　)(A)　　　　　  (B)　　　　　　　 (C)　　　　　　  (D)值不确定

21、一个等差数列共有2n项，奇数项的和与偶数项的和分别为24和30，且末项比首项大10.5，则该数列的项数是　　　　　　　　　　　　　　　　 (　　)

(A)4　　　　　　  (B)8　　　　　　  (C)12　　　　　　  (D)20

22、等差数列{a_n}中如果a₆=6，a₉=9，那么a₃=　　　　　　　　　　　  (　　)

(A)3　　　　　　  (B)　　　　　　　 (C)　　　　　　　 (D)4

23、设{a_n}是等比数列，且a₁=，S₃=，则它的通项公式为a_n=　　　　  (　  )

(A)　(B)　(C)　(D)或

24、已知a、b、c、d是公比为2的等比数列，则=　　　　　　　　 (　　)

(A)1　　　　　　　 (B)　　　　　　　　(C)　　　　　　　 (D)

25、已知等比数列{a_n} 的公比为q，若=m（n为奇数），则=　　　(　　)

(A)mq^n－1 　　　　(B) mqⁿ 　　　　　 (C) mq 　　　　　 (D)

26、已知等比数列前10项的和为10，前20项的和为30，那么前30项的和为(　　)

(A)60　　　　　 (B)70　　　　　　 (C)90　　　　　　  (D)126

27、若{a_n}是等比数列，已知a₄ a₇=－512，a₂+a₉=254，且公比为整数，则数列的a₁₂是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　)

(A)－2048　　　　  (B)1024　　　　　  (C)512　　　　　 (D)－512

28、数列{a_n}、{b_n}都是等差数列，它们的前n项的和为，则这两个数列的第5项的比为　　　　　　　　 (　　)

(A)　　　　(B)　　　　　 (C)　　　　　 (D)以上结论都不对

29、已知，则a，b，c　　　　　　　　　　　　　　　 (　　)

(A)成等差数列　　　　　　　　　　　 (B)成等比数列

(C)既成等差数列又成等比数列　　　　 (D)既不成等差数列又不成等比数列

30、若a+b+c，b+c－a，c+a－b，a+b－c成等比数列，且公比为q，则q³+q²+q的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　  )(A)1　　　　　  (B)－1　　　　　　　 (C)0　　　　　　  (D)2

31、若一等差数列前四项的和为124，后四项的和为156，又各项的和为350，则此数列共有　　　　　　　　　　　　　　　　　　　　　　　　　　  (　　)

(A)10项　　　　  (B)11项　　　　　 (C)12项　　　　　 (D)13项

32、在3和9之间插入两个正数，使前三个数成等比数列，后三个数成等差数列，则二数之和为　　　　　　　　　　　　　　　　　　　　　　　  (　　)

(A)　　　　　 (B)　　　　　 (C)　　　　　  (D)

33、数列1，，，……，的前n项和为　　　　 (　　)

(A) 　　　　　(B)　　　　 (C)　　　　 (D)

34、设数列{a_n}各项均为正值，且前n项和S_n=（a_n+），则此数列的通项a_n应为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　)

(A) a_n=　　　　　　　　　　　　  (B) a_n=

(C) a_n=　　　　　　　　　　　 (D) a_n=

35、数列{a_n}为等比数列，若a₁+ a₈=387，a₄ a₅=1152，则此数列的通项a_n的表达式为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  (　　)

(A) a_n =3×2^{n -1}  (B) a_n =384×（）^{n -1}

(C) a_n =3×2^{n -1}或a_n =384×（）^{n -1}　　　　(D) a_n =3×（）^{n -1}

36、已知等差数{a_n}中，a₃+ a₄+ a₅+ a₆+ a₇=450，则a₁+ a₉=　　　　　　　 (　　)

(A)45　　　　　  (B)75　　　　　  (C)180　　　　　　 (D)300

37、已知等比数列{a_n}中，a_n＞0，公比q≠1，则　　　　　　　　　  (　　)

(A)　　　　　　　　  (B)

(C)　　　　　　　  (D)

38、在等比数列中，首项，末项，公比，求项数　　　　　　　  (　　)

(A)3　　　　　  (B)4　　　　　　 (C)5　　　　　　 (D)6

39、等比数列{a_n}中，公比为2，前四项和等于1，则前8项和等于　　  (　　)

(A)15　　　　　　 (B)17　　　　　　  (C)19　　　　　　  (D)21

40、某厂产量第二年增长率为p，第三年增长率为q，第四年增长率为r，设这三年增长率为x，则有　　　　　　　　　　　　　　　　　　　　　　 (　　)

(A)　　　　　　　　　　　　　(B)

(C)　　　　　　　　　　　　  (D)

二、填空题　　　　

1、已知等差数列公差d＞0,a₃a₇=－12,a₄+a₆=－4,则S₂₀=_______

2、数列{a_n}中，若a₁,a₂,a₃成等差数列,a₂,a₃,a₄成等比数列,a₃,a₄,a₅的倒数又成等差数列，则a₁,a₃,a₅成_______数列

3、已知{a_n}为等差数列,a₁=1,S₁₀=100,a_n=_______.令a_n=log₂b_n,则的前五项之和

S₅′=_______

4、已知数列则其前n项和S_n=________.

5、数列前n项和为S_n=n²+3n,则其通项a_n等于____________.

6、等差数列{a_n}中, 前4项和为26, 后4项之和为110, 且n项和为187, 则n的值为____________.

7、已知等差数列{a_n}的公差d≠0, 且a₁,a₃,a₉成等比数列, 的值是________.

8、等差数列{a_n}中, S₆=28, S₁₀=36(S_n为前n项和), 则S₁₅等于________.

9、等比数列{a_n}中, 公比为2, 前99项之和为56, 则a₃+a₆+a₉+…a₉₉等于________.

10、等差数列{a_n}中, a₁=1,a₁₀=100,若存在数列{b_n}, 且a_n=log₂b_n,则b₁+b₂+b₃+b₄+b₅等于____________.

11、已知数列1, , 前n项的和为____________.

12、已知{a_n}是等差数列,且有a₂+a₃+a₁₀+a₁₁=48, 则a₆+a₇=____________.

13、等比数列{a_n}中, a₁+a₂+a₃+a₄=80, a₅+a₆a₇+a₈=6480, 则a₁必为________.

14、三个数、1、成等差数列，而三个数a²、1、c²成等比数列， 则等于____________.

15、已知, lgy成等比数列, 且x＞1,y＞1, 则x、y的最小值为________.

16、在数列{a_n}中, , 已知{a_n}既是等差数列, 又是等比数列,则{a_n}的前20项的和为________.

17、若数列{a_n},  (n∈N), 则通项a_n=________.

18、已知数列{a_n}中, (n≥1), 则这个数列的通项公式a_n=________.

19、正数a、b、c成等比数列, x为a、b的等差中项, y为b、c的等差中项, 则的值为________.

20、等比数列{a_n}中, 已知a₁·a₂·a₃=1,a₂+a₃+a₄=, 则a₁为________.

三、解答题　　　　

1、在等差数列{a_n}中,a₁=－250,公差d=2,求同时满足下列条件的所有a_n的和,

(1)70≤n≤200;(2)n能被7整除.

翰林汇

2、设等差数列{a_n}的前n项和为S_n.已知a₃=12, S₁₂＞0,S₁₃＜0.(Ⅰ)求公差d的取值范围；

(Ⅱ)指出S₁,S₂,…,S₁₂,中哪一个值最大,并说明理由.

翰林汇

3、数列{}是首项为23，公差为整数的等差数列，且前6项为正，从第7项开始变为负的，回答下列各问：(1)求此等差数列的公差d;(2)设前n项和为,求的最大值;(3)当是正数时,求n的最大值.

翰林汇

4、设数列{}的前n项和.已知首项a₁=3,且+=2,试求此数列的通项公式及前n项和.

5、已知数列{}的前n项和n(n＋1)(n＋2),试求数列{}的前n项和.

6、已知数列{}是等差数列,其中每一项及公差d均不为零,设=0(i=1,2,3,…)是关于x的一组方程.回答：(1)求所有这些方程的公共根;

(2)设这些方程的另一个根为,求证,,,…, ,…也成等差数列.

7、如果数列{}中,相邻两项和是二次方程=0(n=1,2,3…)的两个根,当a₁=2时,试求c₁₀₀的值.

翰林汇

8、有两个无穷的等比数列{}和{},它们的公比的绝对值都小于1,它们的各项和分别是1和2,并且对于一切自然数n,都有,试求这两个数列的首项和公比.

翰林汇

9、有两个各项都是正数的数列{},{}.如果a₁=1,b₁=2,a₂=3.且,,成等差数列, ,,成等比数列,试求这两个数列的通项公式.

10、若等差数列{log₂x_n}的第m项等于n，第n项等于m(其中m¹n)，求数列{x_n}的前m＋n项的和。

数列复习题 〈答卷〉

一、选择题　　　　

1、　A 翰林汇2、　C  翰林汇3、 B 、 4、C  翰林汇5、  A　翰林汇6、　C 7、　C　翰林汇8、　D  翰林汇9、　C 10、 C　翰林汇

11、 D 12、 B 13、 C 14、  A 15、  B　翰林汇16、 B　翰林汇17、 D 18、　D  翰林汇19、 D翰林汇　20、 B

翰林汇21、　B　翰林汇22、 A　翰林汇23、 D　翰林汇24、 C　翰林汇25、 B 26、 B　翰林汇27、 A　翰林汇28、 C 翰林汇29、 B 30、

A 31、 A32、　B 33、 D34、 B 35、 C翰林汇36、 C 翰林汇37、 A 38、 B 翰林汇39、 B 翰林汇40、 C  翰林汇

二、填空题　　　　

1、 1802、　等比3、　2n－1,翰林汇4、 5、　2n+2.翰林汇6、 11.翰林汇7、翰林汇8、24翰林汇9、32

10、 682翰林汇11、翰林汇12、24翰林汇13、－4或2. 14、 1或翰林汇15、16、100. 17、

18、翰林汇19、2.20、 2或

三、解答题　　　　

1、 解： a₁=－250, d=2, a_n=－250+2(n－1)=2n－252

同时满足70≤n≤200, n能被7整除的a_n构成一个新的等差数列{b_n}.

b₁=a₇₀=－112, b₂=a₇₇=－98,…, b_n′=a₁₉₆=140

其公差d′=－98－(－112)=14. 由140=－112+(n′－1)14, 解得n′=19

∴{b_n}的前19项之和.

2、解： (Ⅰ)依题意,有

，即

由a₃=12,得　a₁=12－2d　 (3)

将(3)式分别代入(1),(2)式,得　，∴.

(Ⅱ)由d＜0可知 a₁＞a₂＞a₃＞…＞a₁₂＞a₁₃.

因此,若在1≤n≤12中存在自然数n,使得a_n＞0,a_n+1＜0,则S_n就是S₁,S₂,…,S₁₂中的最大值.

由于　S₁₂=6(a₆+a₇)＞0,　S₁₃=13a₇＜0，即 a₆+a₇＞0, a₇＜0.

由此得　a₆＞－a₇＞0.因为a₆＞0, a₇＜0,故在S₁,S₂,…,S₁₂中S₆的值最大.

3、 (1)由a₆=23＋5d＞0和a₇=23＋6d＜0,得公差d=－4.(2)由a₆＞0,a₇＜0,∴S₆最大, S₆=8.(3)由a₁=23,d=－4,则=n(50－4n),设＞0，得n＜12.5,整数n的最大值为12.

4、∵a₁=3, ∴S₁=a₁=3.在S_n+1＋S_n=2a_n+1中,设n=1,有S₂＋S₁=2a₂.而S₂=a₁＋a₂.即a₁＋a₂＋a₁=2a₂.∴a₂=6. 由S_n+1＋S_n=2a_n+1,……(1)　S_n+2＋S_n+1=2a_n+2,……(2)

(2)－(1),得S_n+2－S_n+1=2a_n+2－2a_n+1，∴a_n+1＋a_n+2=2a_n+2－2a_n+1

即　 a_n+2=3a_n+1

此数列从第2项开始成等比数列,公比q=3.a_n的通项公式a_n=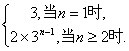

此数列的前n项和为S_n=3＋2×3＋2×3²＋…＋2×3^{n – 1}=3＋=3ⁿ.

5、=－=n(n＋1)(n＋2)－(n－1)n(n＋1)=n(n＋1).当n=1时，a₁=2,S₁=×1×(1＋1)×(2＋1)=2,∴a₁= S₁.则＝n(n＋1)是此数列的通项公式。∴＝1－＝.

6、 (1)设公共根为p,则①②则②-① ,得dp²+2dp+d=0,d≠0为公差,∴(p＋1)²=0.∴p=－1是公共根.(直接观察也可以看出公共根为－1).(2)另一个根为,则＋(－1)=.∴+1= 即,易于证明{}是以－为公差的等差数列.

7、解由根与系数关系, ＋=－3n,则(＋)－(＋)=－3,即－=－3.∴a₁,a₃,a₅…和a₂,a₄,a₆…都是公差为－3的等差数列,由a₁=2,a₁+a₂=－3,∴a₂=－5.则=－3k－2,∴a₁₀₀=－152, =－3k＋5,∴a₁₀₁=－148,∴c₁₀₀= a₁₀₀ a₁₀₁=22496

8、设首项分别为a和b,公比q和r. 则有.依据题设条件,有=1,① =2,② ,③ 由上面的①,②,③ 可得(1－q)²=2(1－r).令n=1,有(1－q)²=2(1－r),④设n=2.则有(1－q)²q²=2(1－r)r,⑤ 由④和⑤,可得q²=r,代入④ 得(1－q)²=2(1－q²).由于q≠1,∴有q=,r =.因此可得a=1－q=,b=2(1－r)=.

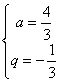∴和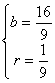经检验,满足的要求.

9、依据题设条件,有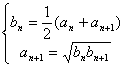由此可得=.∵＞0,则2。∴{}是等差数列.∴=.

又　=,∴=

10、2^m+n-1

翰林汇