高一第一学期数学质量调研测试卷（样卷）

　　　　高一第一学期数学质量调研测试卷（样卷）　　　

试卷说明：

1. 本套试卷分两个部分. A卷试题为必做题，B卷试题为选做题.

2.  A卷满分100分，B卷满分20分.

3. 本套试卷总测试时间为100分钟.

4. 本卷中的部分试题有新老教材之分，请考生解答相应的试题，否则该题不给分.

A卷

题号	一		二			三		A卷总分
	1—10	11—16	17	18	19	20	21
得分

一、填空题（）本大题共有10小题，只要求直接填写结果，每个空格填对得4分，否则一律不给分.

1. 用列举法描述集合{　　　　　　 }.

2. 命题“若，则实数或”的否命题是　　　　　　　　　　　　　　  .

3. 函数的定义域是______________.

4. 函数的最大值为　　　　　　　  .

5. （老教材）若是方程的根，且、均为实数，则　　　　  .

（新教材）若，则__________.

6. 函数的单调递增区间是______________.

7. 关于的方程有两个同号但不相等的实根的一个充要条件是　　　　　　　　　　　  .

8. 如图1所示，用一根长为4米的木料制成窗框，设窗框的宽为米，长为米.若不计木料的厚度与损耗，则将窗的面积S表示成宽的函数为　　　　　　　　　　　　　　　　　　　　　　 .

9. 不等式组的正整数解集为________________.

10. 写出二次函数的图像与轴没有交点的一个充分不必要条件是___________________________.

二、选择题（）本大题共有6小题，每小题有且仅有一个正确的选项，每题选对得4分，选错或不选均不得分.

11. “”是“”的_______条件　　　　　　　　　　　　　　　　　　 （　　　）

A. 充分非必要；　　　　B. 必要非充分；　　  C. 充要；　　 D. 既非充分又非必要.

12. 下列命题中与命题“能被6整除的整数一定能被2整除.”等价的命题是　　　　（　　  ）

　　A. 能被2整除的整数一定能被6整除；　　　

B. 不能被6整除的整数一定不能被2整除；

　　C. 不能被2整除的整数不一定能被6整除；　

D. 不能被2整除的整数一定不能被6整除.

13. 函数是　　　　　　　　　　　　　　　　　　　　　 （　　　）

　　A. 奇函数；　　 B. 偶函数；　　 C. 非奇非偶函数；　 D. 既是奇函数又是偶函数.

14. 若，则下列不等式中不一定成立的是　　　　　　　　　　　　　　　　  （　　　）

　　A. ；　 B. ；　 C. ；　　D. .

15. （老教材）下列命题中正确的是　　　　　　　　　　　　　　　　　　　　　　 （　　　）

A. 任何两个复数都可以比较大小；　　　　  B. 任意两个虚数的积一定是虚数；

C. 两个共轭复数的差是纯虚数；　　　　　  D. 任意一个纯虚数的平方一定是负实数.

　　（新教材）函数的图像一定不经过　　　　　　　　　　　　　　　　 （　　　）

　　A. 第一象限；　　 B. 第二象限；　　　　 C. 第三象限；　　　　 D. 第四象限.

16. 已知，则关于表达式，下列说法正确的是　　　　　　　　　　　  （　　　）

A．有最小值； B．有最小值4；　 C．有最小值；　　 D．有最大值4.

三、简答题（）本大题共有3题，解答下列各题必须写出必要的步骤.

17.（本题满分6分）求证：函数在区间上单调递减.

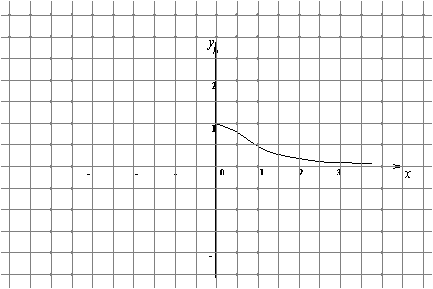
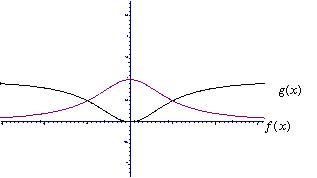
18．（本题满分6分）函数的图像如右图（图2）所示，试解不等式.

19．（本题满分6分）建筑学规定，民用住宅的居室窗户面积必须小于该室内地面面积.同时，按室内采光标准，住宅的居室窗户面积与该室内地面面积之比不小于10%，并且这个比值越大，住宅的采光条件就越好.现在若同时增加相同的窗户面积和地面面积，住宅的采光条件是变好了还是变坏了？请说明你的理由.

四、解答题（）本大题共有2题，解答下列各题必须写出必要的步骤.

20．（本题满分8分）

（老教材）已知复数，若存在实数，使得成立，求的取值范围.

（新教材）若关于的方程有实根，求实数的取值范围.

21.（本题满分10分，其中第1小题3分，第2小题3分，第3小题4分）

已知函数，令.

（1）求函数的值域；

（2）任取定义域内的5个自变量，根据要求计算并填表；观察表中数据间的关系，猜想一个等式并给予证明；

						…
						…
						…

（3）如图，已知在区间的图像，请据此在该坐标系中补全函数在定义域内的图像，并在同一坐标系中作出函数的图像. 请说明你的作图依据.

B卷

题号	一	三	总分
	1～3	4
得分

一、填空题（）本大题共有2小题，只要求直接填写结果，每个空格填对得3分，否则一律不给分.

1. 已知函数不是一次函数，它的定义域和值域都为.且同时满足条件：

（1），；

（2）对定义域内任意的实数、，若则.

试写出一个满足以上条件的函数的解析式　　　　　　　　　　  .

2. 若对于两个实数集合、，

集合的运算定义为： ；

集合的运算定义为： .

已知实数集合，.试写出一个实数，使得但，则　　　　　　  .

二、选择题（）本大题共有1小题，每小题有且仅有一个正确的选项，选对得3分，选错或不选均不得分.

3. 设A、B是两个非空集合，若规定：,则 （　　　）

A. ；　　　　　　　 B. ；　　　 C. ；　　　　  D. .

三、解答题（）本大题共有1题，解答下列各题必须写出必要的步骤.

4.（本题满分11分）

已知二次函数（a，b，c均为常数，且a≠0）满足条件且方程有两个等根.

（1）求函数的解析式；

（2）试确定一个区间P，使得在P内单调递减且不等式在P内恒成立；

（3）是否存在这样的实数、（），使得在区间内的取值范围恰好是？如果存在，试求出、的值；如果不存在，请说明理由.

高一调研样卷参考解答

A卷

一、填空题：

1.  0，1，2，3 ；　 2. 若，则实数且.　3.  ；　 4.　1；

5. （老教材） 0 （新教材） 3 ；　6. （左侧为开区间亦算对）； 7. ；　8. ，　9. 　10. 开放题，可填等；

二、选择题：

11A  12D　13B　14.C　 15（老）D；（新）B； 16A

三、简答题：

17. 证：任取， 有 因为，所以，，即 所以，函数在区间上单调递减.
18. 解：的图像关于原点对称，　　是奇函数 　　 即， 由图像可知， 结合图形即可得出不等式的解集为.
19解：设住宅的窗户面积为a，地板面积为b，令窗户增大的面积和地板增大的面积都是m。 由已知得且 　　因为， 　　 　 故住宅的采光条件变好了。
四、解答题： 20.（老教材） 解：由 得到　　　 　 　　　　  . 注：将参数直接代入求最值可参照给分.
20.（新教材）令，原方程即为. ， ，当且仅当时等号成立. 故实数的取值范围是.
21. （1）解：由条件，的定义域为一切实数，故 　　 所以，. （2）表格内数据只要满足和互为相反数即可得分. 猜想：或 证明： (3) 和的图象见下图. 因为，且，，所以函数和都是偶函数，其本身图象关于轴对称. （注：只作对图象，并说明了理由的可得2分） 又所以函数的图象和的图象关于轴对称，即图象和图象关于直线对称.由此，可作出和在定义域内的全部图象. （注：若说明采用描点法作图且图象基本正确，但没有对性质加以研究的解答可适当给分，但不给满分.函数图像中的点不挖去也不扣分）

B卷

B1开放题，可填，等（注：此处没有加定义域不扣分）.

B2本题为开放题，可填“”等

B3 B

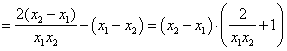
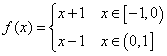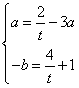
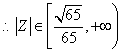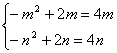
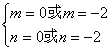B4. 解：(1) 由知此函数图像的对称轴方程为，且. 又由方程有等根，∴△，得. 再由，可得.故. (2), 函数图像的对称轴方程为 　且图像开口向下，所以若要在P内单调递减， 　又在P内恒成立， 　 综上所述：P=. （注：开放题，答案可以是在区间内的非空区间） (3) ，，即. 而抛物线的对称轴为，∴当时，在上为增函数. 若满足题设条件的存在，则 即， 又，，这时，定义域为，值域为。 所以，满足条件的存在，.