向量与三角综合题选
1.将函数y=f(x)·cosx的图象按向量a=(![]() ,1)平移,得到函数y=2sin2x的图象那么函数
,1)平移,得到函数y=2sin2x的图象那么函数
f(x)可以是 ( D )
A.cosx B.2cosx C.sinx D.2sinx
2.已知![]()
![]() ,
,![]()
![]() (
(![]() ),且
),且![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]() (
(![]() ),则
),则![]()
![]() .
.
3.已知向量![]()
①![]() ;
;
②若![]()
解:(1)![]()
![]()
![]()
(2)![]()
![]()
①当![]() 时,当县仅当
时,当县仅当![]() 时,
时,![]() 取得最小值-1,这与已知矛盾;
取得最小值-1,这与已知矛盾;
②当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,由已知得
,由已知得
![]() ;
;
③当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,由已知得
,由已知得![]()
解得![]() ,这与
,这与![]() 相矛盾,综上所述,
相矛盾,综上所述,![]() 为所求。
为所求。
4.平面直角坐标系内有点P![]()
(Ⅰ)求向量![]() 的夹角
的夹角![]() 的余弦用x表示的函数
的余弦用x表示的函数![]() ;
;
(Ⅱ)求![]() 的最小值.
的最小值.
解:(Ⅰ)![]()
(Ⅱ)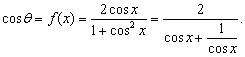
![]() .
.
![]() .
.
5.设![]() ,
,![]() ,
,![]()
![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() ,且
,且![]() ,求
,求![]() 的值.(本题12分)
的值.(本题12分)
.解:
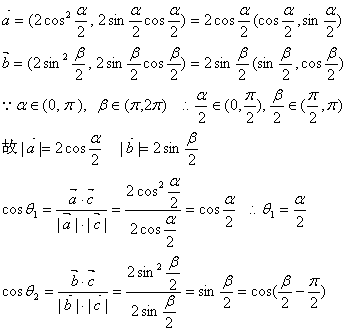
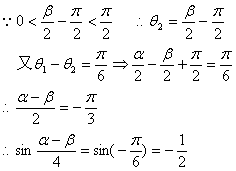
6.已知函数![]() 、b为常数,且
、b为常数,且![]() )的图象过点(
)的图象过点(![]() ),且函数
),且函数![]() 的最大值为2.
的最大值为2.
(1)求函数![]() 的解析式,并写出其单调递增区间;
的解析式,并写出其单调递增区间;
(2)若函数![]() 的图象按向量
的图象按向量![]() 作移动距离最小的平移后,使所得的图象关于y轴对称,求出向量
作移动距离最小的平移后,使所得的图象关于y轴对称,求出向量![]() 的坐标及平移后的图象对应的函数解析式
的坐标及平移后的图象对应的函数解析式
解:(1)![]()
![]()
所以函数![]() 的解析式是
的解析式是![]()
![]() 的单调递增区间是
的单调递增区间是![]()
(2)∵平移后的图象对应的函数解析式是![]()
图象关于y轴对称,即![]() 为偶函数,
为偶函数,
![]()
![]() 恒成立
恒成立
![]()
![]() ,
,
![]()
故![]()
![]() ,图象对应的函数解析式为
,图象对应的函数解析式为![]()
7.已知二次函数![]() 对任意
对任意![]() ,都有
,都有![]() 成立,设向量
成立,设向量![]() (sinx,2),
(sinx,2),![]() (2sinx,
(2sinx,![]() ),
),![]() (cos2x,1),
(cos2x,1),![]() (1,2),当
(1,2),当![]() [0,
[0,![]() ]时,求不等式f(
]时,求不等式f(![]() )>f(
)>f(![]() )的解集.
)的解集.
解析:设f(x)的二次项系数为m,其图象上两点为(1-x,![]() )、B(1+x,
)、B(1+x,![]() )因为
)因为![]() ,
,![]() ,所以
,所以![]() ,由x的任意性得f(x)的图象关于直线x=1对称,若m>0,则x≥1时,f(x)是增函数,若m<0,则x≥1时,f(x)是减函数.
,由x的任意性得f(x)的图象关于直线x=1对称,若m>0,则x≥1时,f(x)是增函数,若m<0,则x≥1时,f(x)是减函数.
∵ ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,
∴ 当![]() 时,
时,![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() .
.
∵ ![]() , ∴
, ∴ ![]() .
.
当![]() 时,同理可得
时,同理可得![]() 或
或![]() .
.
综上:![]() 的解集是当
的解集是当![]() 时,为
时,为![]() ;
;
当![]() 时,为
时,为![]() ,或
,或![]() .
.
8.平面直角坐标系有点![]()
(1)求向量![]() 的夹角θ的余弦用x表示的函数f(x);
的夹角θ的余弦用x表示的函数f(x);
(2)求θ的最值.
解:(1)![]()
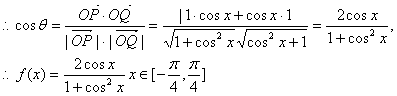
(2)![]()

9.如图:已知△OFQ的面积为![]() ,且
,且![]() ,
,
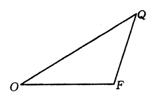
(1)若![]() 时,求向量
时,求向量![]() 与
与![]() 的夹角
的夹角![]() 的取值范围;
的取值范围;
(2)设![]() ,
,![]() 时,若以O为中心,F为焦点的双曲线经过点Q,当
时,若以O为中心,F为焦点的双曲线经过点Q,当![]() 取得最小值时,求此双曲线的方程.
取得最小值时,求此双曲线的方程.
(1)
由已知,得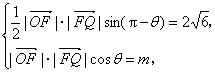 所以
所以![]() ,因为
,因为![]() ,所以
,所以![]() ,则
,则![]() . (2)以O为原点,
. (2)以O为原点,![]() 所在直线为x轴建立直角坐标系,设所求的双曲线方程为
所在直线为x轴建立直角坐标系,设所求的双曲线方程为![]() ,(a>0,b>0),Q点的坐标为(
,(a>0,b>0),Q点的坐标为(![]() ,
,![]() ),则
),则![]() =(
=(![]() ,
,![]() ),因为△OFQ的面积
),因为△OFQ的面积![]() ,所以
,所以![]() ,又由
,又由![]() (c,0)(
(c,0)(![]() ,
,![]() )
)![]() ,所以
,所以![]() ,
,![]() ,当且仅当c=4时,
,当且仅当c=4时,![]() 最小,此时Q的坐标为(
最小,此时Q的坐标为(![]() ,
,![]() ),由此可得
),由此可得 解之得
解之得 故所求的方程为
故所求的方程为![]()
10. 已知向量![]() ,
,![]() ,且
,且![]()
(1) 求![]() 及
及![]() ;
;
(2) 求函数![]()
![]() +
+![]() 的最大值,并求使 函数 取得最大值的x的值。
的最大值,并求使 函数 取得最大值的x的值。
解(1)![]() -
-![]() =
=![]()
![]() =
=
=![]()
=![]() =2
=2![]()
∵![]()
∴ ![]() =-2
=-2![]()
(2)![]()
![]() +
+![]() =
=![]() -2
-2![]()
=![]()
=![]()
∵![]()
∴-1≤![]() ≤0 ∴-1≤
≤0 ∴-1≤![]() ≤3
≤3
∴当![]() =-1时
=-1时 ![]() =3,此时
=3,此时![]() (∵
(∵![]() )。
)。
11.已知向量![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 与
与![]() 之间有关系式:
之间有关系式:![]() ,其中k>0.
,其中k>0.
(1)试用k表示![]() ;
;
(2)求![]() 的最小值,并求此时
的最小值,并求此时![]() 与
与![]() 的夹角
的夹角![]() 的值.
的值.
(1)因为![]() ,所以
,所以![]() ,
,![]()
![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]() . (2)由(1)
. (2)由(1)![]()
![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时取等号.此时,
时取等号.此时,![]()
![]() ,
,![]() ,
,![]() ,所以
,所以![]() 的最小值为
的最小值为![]() ,此时
,此时![]() 与
与![]() 的夹角
的夹角![]() 为
为![]()
12.已知向量![]() ,
,![]() ,又二次函数
,又二次函数![]() 的开口向上,其对称轴为
的开口向上,其对称轴为![]() ,当
,当![]() 时,求使不等式
时,求使不等式![]() 成立的
成立的![]() 的范围。
的范围。
.依题意有,当x≥1时,f(x)是增函数
∵![]()
![]()
∴![]()
![]()
∵0≤x≤π ![]() 即为所求
即为所求
13.已知=(sinA,cosA), =(cosC,sinC),若·=sin2B, ,的夹角为θ,且A、B、C为三角形ABC的内角。
求(1)∠B (2)cos
解:(1)由·=sin2B得
sinAcosC+cosAsinC=2sinBcosB
所以 sin(A+C)=2sinBcosB
又在△ABC中,A+C=π-B,sin(A+C)≠0
所以sinB=2sinBcosB
即:cosB=,所以B=
(2)cosθ===sin(A+C)
∵在△ABC中,B=,A+C=
∴cosθ=sin=
∴cos2===
∵0<θ<π,∴cos=
14. 已知平面向量![]() ,
,![]() ,若存在非零实数
,若存在非零实数![]() 和角
和角![]() ,
,![]() ,使得
,使得![]() ,
,![]() ,且
,且![]() 。
。
⑴若![]() 时,求
时,求![]() 的值;
的值;
⑵若![]() 在
在![]() 上变化时,求
上变化时,求![]() 的极大值。
的极大值。
解:⑴∵![]()
从而![]() =
=![]()
=![]()
则![]() 而
而![]() 于是∴
于是∴![]()
⑵令 ![]() ,则
,则![]() ,求导有:
,求导有:
![]()
在![]() 时,
时,![]() ,
,![]() 或
或![]() 时,
时,![]()
∴在![]() 时,
时,![]() 取极大值,
取极大值,![]()
因此![]() 的极大值为
的极大值为![]()
15. 已知向量![]() ,求
,求
①![]() ;
;
②若![]() 的最小值是
的最小值是![]() ,求实数
,求实数![]() 的值;
的值;
解:①a·b=![]()
a+b=![]() ,
,
∵![]() , ∴
, ∴![]() ∴ a+b=2cosx.
∴ a+b=2cosx.
②![]() 即
即![]()
∵![]() , ∴
, ∴![]()
![]() 时,当且仅当
时,当且仅当![]() 取得最小值-1,这与已知矛盾.
取得最小值-1,这与已知矛盾.
![]() 时,当且仅当
时,当且仅当![]() 取最小值
取最小值![]()
由已知得![]() ,解得
,解得![]()
![]() 时,当且仅当
时,当且仅当![]() 取得最小值
取得最小值![]()
由已知得![]() ,解得
,解得![]() ,这与
,这与![]() 相矛盾.
相矛盾.
综上所述,![]() 为所求.
为所求.
16.已知在三角形ABC中,∠A、∠B、∠C成等差数列,![]() =2
=2![]() ,
,![]()
(1)求三角形ABC的面积;
(2)求三角形ABC的周长。