
2004-2005学年度上学期
高中学生学科素质训练
新课标高一数学同步测试(1)—第一单元(集合)
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.下列各项中,不可以组成集合的是 ( )
A.所有的正数 B.约等于2的数 C.接近于0的数 D.不等于0的偶数
2.已知集合![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A.1 B.—1 C.1或—1 D.1或—1或0
3.设集合![]() ,
,![]() ,
,![]() ,若
,若![]() ,则
,则![]() ( )
( )
A.![]() B.
B. ![]() C
.
C
.![]() D.
D.![]()
4.设![]() ={1,2,3,4} ,若
={1,2,3,4} ,若![]() ={2},
={2},![]() ,
,![]() ,则下列结论正确的是 ( )
,则下列结论正确的是 ( )
A.![]() 且
且![]() B.
B.![]() 且
且![]()
C.![]() 且
且![]() D.
D.![]() 且
且![]()
5.以下四个关系:![]()
![]() ,
,![]()
![]() ,{
,{![]() }
}![]() ,
,![]()
![]()
![]() ,其中正确的个数是 ( )
,其中正确的个数是 ( )
A.1 B.2 C.3 D.4
6. 设![]() 为全集,
为全集,![]() 为非空集合,且
为非空集合,且![]()
![]()
![]()
![]()
![]() ,下面结论中不正确的是 ( )
,下面结论中不正确的是 ( )
A.![]() B.
B.![]()
![]()
C.![]() D.
D.![]()
![]()
7.下列四个集合中,是空集的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.设集合![]() ,
,![]() ,则 ( )
,则 ( )
A.![]() B.
B.![]()
![]()
![]() C.
C.![]()
![]()
![]() D.
D.![]()
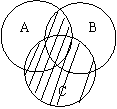 9.表示图形中的阴影部分( )
9.表示图形中的阴影部分( )
![]() A.
A.![]()
B.![]()
C.![]()
D.![]()
10.已知集合A、B、C为非空集合,M=A∩C,N=B∩C,P=M∪N,则 ( )
A.C∩P=C B.C∩P=P C.C∩P=C∪P D.C∩P=![]()
二、填空题:请把答案填在题中横线上(每小题6分,共24分).
11.若集合![]() ,则
,则![]() .
.
12.设集合![]() ,
,![]() ,则方程
,则方程![]()
![]() 的解集为
.
的解集为
.
13.已知集合![]() 至多有一个元素,则a的取值范围
.
至多有一个元素,则a的取值范围
.
14.已知![]() ,
,![]() ,则B=
.
,则B=
.
三、解答题:解答应写出文字说明、证明过程或演算步骤(共76分).
15.(12分)已知集合A={xx=m2-n2,m∈Z,n∈Z}
求证:(1)3∈A;
(2)偶数4k—2 (k∈Z)不属于A.
16.(12分)(1)P={xx2-2x-3=0},S={xax+2=0},S![]() P,求a取值?
P,求a取值?
(2)A={-2≤x≤5} ,B={xm+1≤x≤2m-1},B![]() A,求m?
A,求m?
17.(12分)在1到100的自然数中有多少个能被2或3整除的数?
18.(12分)已知方程![]() 的两个不相等实根为
的两个不相等实根为![]() 。集合
。集合![]() ,
,
![]() {2,4,5,6},
{2,4,5,6},![]() {1,2,3,4},A∩C=A,A∩B=
{1,2,3,4},A∩C=A,A∩B=![]() ,求
,求![]() 的值?
的值?
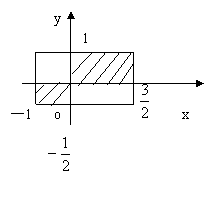
19.(14分)用描述法表示图中的阴影部分(包括边界)
 |
20. (14分)设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为自然数,A={
为自然数,A={![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() },B={
},B={![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() },且
},且![]() <
<![]() <
<![]() <
<![]() <
<![]() ,并满足A∩B={
,并满足A∩B={![]() ,
,![]() },
},![]() +
+![]() =10,A∪B中各元素之和为256,求集合A?
=10,A∪B中各元素之和为256,求集合A?
参考答案
一、DDCBA BDBAB
二、11.2; 12.A∪B; 13.a =0或![]() ; 14.{0,1,2}
; 14.{0,1,2}
三、15.证明:(1)3=22-12
∴3![]() A
A
(2)设4k-2![]() A,得存在m,n
A,得存在m,n![]() Z,使4k-2=m2-n2成立. (m-n)(m+n)=4k-2
Z,使4k-2=m2-n2成立. (m-n)(m+n)=4k-2
当m,n同奇或同偶时,m-n,m+n均为偶数
∴(m-n)(m+n)为4的倍数,与4k-2不是4 倍数矛盾.
当m,n同分别为奇,偶数时,m-n,m+n均为奇数
(m-n)(m+n)为奇数,与4k-2是偶数矛盾.∴4k-2![]() A
A
16.解:(1)a=0,S=![]() ,
,![]()
![]() P成立 a
P成立 a![]() 0,S
0,S![]()
![]() ,由S
,由S![]() P,P={3,-1}
P,P={3,-1}
得3a+2=0,a=-![]() 或-a+2=0,a=2; ∴a值为0或-
或-a+2=0,a=2; ∴a值为0或-![]() 或2.
或2.
(2)B=![]() ,即m+1>2m-1,m<2
,即m+1>2m-1,m<2 ![]()
![]() A成立.
A成立.
B≠![]() ,由题意得
,由题意得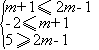 得2≤m≤3
得2≤m≤3![]()
∴m<2或2≤m≤3 即m≤3为取值范围.
注:(1)特殊集合![]() 作用,常易漏掉
作用,常易漏掉
(2)运用分类讨论思想,等价转化思想,数形结合思想常使集合问题简捷比.
17.解:设集合A为能被2整除的数组成的集合,集合B为能被3整除的数组成的集合,则![]() 为能被2或3整除的数组成的集合,
为能被2或3整除的数组成的集合,![]() 为能被2和3(也即6)整除的数组成的集合.
为能被2和3(也即6)整除的数组成的集合.
显然集合A中元素的个数为50,集合B中元素的个数为33,集合![]() 中元素的个数为16,可得集合
中元素的个数为16,可得集合![]() 中元素的个数为50+33-16=67.
中元素的个数为50+33-16=67.
18.解:由A∩C=A知A![]() C。又
C。又![]() ,则
,则![]() ,
,![]() . 而A∩B=
. 而A∩B=![]() ,故
,故![]() ,
,![]() 。
。
显然即属于C又不属于B的元素只有1和3. 不仿设![]() =1,
=1,![]() =3. 对于方程
=3. 对于方程![]() 的两根
的两根![]() 应用韦达定理可得
应用韦达定理可得![]() .
.
19.解:![]()
20.由A∩B={![]() ,
,![]() },且
},且![]() <
<![]() <
<![]() <
<![]() <
<![]() .
.
所以只可能![]() =
=![]() ,即
,即![]() =1. 由
=1. 由![]() +
+![]() =10,得
=10,得![]() =9.
=9.
且![]() =9=
=9=![]() (
(![]() ),
),![]() =3或
=3或![]() =3.
=3.
Ⅰ.![]() =3时,
=3时,![]() =2,此时A={1,2,3,9,
=2,此时A={1,2,3,9,![]() },B={1,4,9,81,
},B={1,4,9,81,![]() }.
}.
因![]()
![]()
![]() ,故1+2+3+9+4+
,故1+2+3+9+4+![]() +81+
+81+![]() =256,从而
=256,从而![]() +
+![]() -156=0,解得
-156=0,解得![]() =12.略
=12.略
Ⅱ.![]() =3时,此时A={1,3,
=3时,此时A={1,3,![]() ,9,
,9,![]() },B={1, 9,
},B={1, 9, ![]() , 81,
, 81,![]() }.
}.
因1+3+9+![]() +
+![]() +81+
+81+![]() +
+![]() =256,从而
=256,从而![]() +
+![]() +
+![]() +
+![]() -162=0.
-162=0.
因为![]() <
<![]() <
<![]() ,则3<
,则3<![]() <9. 当
<9. 当![]() =4、6、7、8时,
=4、6、7、8时,![]() 无整数解.
无整数解.
当![]() =5时,
=5时,![]() =11. 略.
=11. 略.