广西南宁02-03年上学期高一数学期中考试
一、选择题（每小题3分，共36分）
1．下列能表示集合的是（ ）
（A）很大的数 （B）聪明的人 （C）大于
的数 （D）某班学习好的同学
2．不等式3≥│5-2x│的解集是（ ）
（A）{x│1≤x≤4} （B）{x│x≤1或x≥4}
（C）{x│-
≤x≤4}
（D）{x│x≤4}
3．设全集U={（x，y）│x∈且y∈R}，A={（x，y）│y=x+1,x≠2}，B={（x,y）│y=x+1}，则（CUA）∩B等于（ ）
（A）φ （B）{（2，3）} （C）（2，3） （D）{2，3}
4．设f：A→B是集合A到B的映射，则下列命题中，正确的命题是（ ）
（A）A中每个元素在B中必有象 （B）B中每个元素在A中必有原象
（C）B中每个元素在A中的原象唯一 （D）A中不同的元素在B中的象必不同
5．当命题“若p则q”为真时，下列命题中一定为真的是（ ）
（A）若q则p （B）若┓p则┓q（C）若┓q则┓p （D）p且q
6．函数y=ax，y=bx，y=cx的图象分别为图中的①②③，
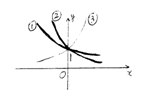则a，b，c的大小关系是（ ）
（A）1＜a＜b＜c （B）a＜b＜c＜1
（C）b＜a＜1＜c （D）a＜b＜1＜c
7．函数y=-
（x≤1）的反函数是（ ）
（A）y=x2-1（-1≤x≤0） （B）y=x2-1（0≤x＜1）
（C）y=1-x2（x≤0） （D）y=1-x2（0≤x≤1）
8．若函数y=（2k+1）x+b在（-∞，+∞）上是减函数，则（ ）
（A）k＞
（B）k＜
（C）k＞-
（D）k＜-
9．复合命题S具有p或q的形式，已知p且r是真命题，那么┓S是（ ）
（A）真命题 （B）假命题 （C）与命题q的真假有关 （D）与命题r的真假有关
10．若f（x+2）=x2，则f（）=（ ）
（A）6 （B）9+6
（C）9-6
（D）7
11．函数y=（
的值域为（ ）
（A）[ 
，1 ] （B）（0，1） （C）
（D）[ 
，5 ]
12．已知p:│2x-3│＞1，q：
＞0，则┓p是┓q的（
）
（A）充分不必要条件 （B）必要不充分条件
（C）充要条件 （D）既不充分也不必要条件
二、填空题（每空4分，共16分）
13．函数y=x+
的定义域是
14．设函数f（x）是定义域在R上的奇函数，当x＜0时，f（x）=x2-3x；则x≥0时，
f（x）= 。
15．函数y=x+
的单调递减区间为
16．设x2+x-2=5，则x-x-1=
三、解答题
17．（6分）计算：（-1.8）0+（1.5）-2·（3
-（0.01）-0.5+9
18．（6分）解不等式x2-3│x│-4＞0
19．（8分）已知f（x）=
，a≠-
，求
（1）f（x）的反函数；（2）若这个函数的图象关于y=x对称，求a的值.
20．（8分）设函数f（x）=x2+2（a-1）x+2在区间
上是减函数，求实数a的取值范围。（解题过程要求画出示意图）