高一数学第二学期期末调研测试

高一数学第二学期期末调研测试

高 一 数 学 试 题

(满分160分，考试时间120分钟)

一、填空题：本大题共14小题，每小题5分，共70分. 不需写出解答过程．请把答案直接填写在答题卡相应位置上.

1．在空间直角坐标系中，线段A B的端点坐标为A(1，0，2)，B(1，－4，4)，则线段AB的中点坐

标为　 ▲　 ．

2．与直线垂直的一条直线的斜率k=　 ▲　 ．

3．如图，一个空间几何体的主视图和左视图都是边长为1的正方形，

俯视图是一个圆，那么这个几何体的侧面积为　 ▲　 ．

4．直线x－y－5＝0被圆x²＋y²－4x＋4y＋6＝0所截得的弦的长为　 ▲　 ．

5． 对于相异三条直线l、m、n和相异两个平面、，给出下列四个命题：

　　①若m∥l ，n∥l ，则m∥n；

 ②若m⊥a ，m∥b， 则a ⊥b；

③若m∥a ，n∥a ，则m∥n；

④若m⊥b ，a ⊥b ，则m∥a.

其中真命题的序号是　 ▲　 ．

6． 在数列{a_n}中，若对n∈N*，总有a₁＋a₂＋…＋a_n＝2ⁿ－1，则a₁²＋a₂²＋…＋a_n²=　 ▲　 ．

7． 设M为平面内以A(4，1)，B(－1，－6)，C(－2，2)三点为顶点的三角形及其内部，当点(x, y)

在区域M上运动时，4x－y的最小值是　 ▲　 ．

8． 设△ABC的内角A、B的对边分别为a、b，且a＝4，b＝，A＝，则B=　 ▲　 ．

9． 设等差数列中，a₈=2000，a₂₀₀₀=8，则a₂₀₀₈=　 ▲　 ．

10．设m≠0，则圆与圆的位置关系是

　 ▲　 ．(请填写“内含”、“内切”、“相交”、“外切”、“外离”之一)

11．设，则当x=　 ▲　 时，函数取得最小值．

12．若△ABC的三个内角A，B，C成等比数列，则B的取值范围是　 ▲　 ．

13．在△ABC中，如果，其中n，那么cosC的最小值等于

　 ▲　 ．

14．一只蚂蚁从棱长为1cm的正方体的表面上某一点P处出发，走遍正方体的每个面的中心的最短

距离d=f(P), 那么d的最大值是　 ▲　 ．

二、解答题：本大题共6小题，共90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．

15．(本小题满分14分)

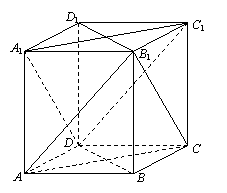
在直四棱柱ABCD－A₁B₁C₁D₁中，底面ABCD是菱形. 求证：

(1)平面B₁AC//平面DC₁A₁;

(2)平面B₁AC⊥平面B₁BDD₁.

16．(本小题满分14分)

如图，在四边形ABCD中，BC=20，DC=40, ．求:

(1)AB;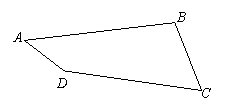

(2)四边形ABCD的面积．

17．(本小题满分15分)

已知无穷等差数列{a_n}的前三项依次为11，14，17．

(1)该数列有多少项在区间[100, 200]上？并求这些项的和；

(2)设，S_n为{b_n}的前n项和，试比较S_n与1的大小．

18．(本小题满分15分)

过点Q 作圆C：x²＋y²＝r²()的切线，切点为D，且QD＝4．

(1)求r的值；

(2)设P是圆C上位于第一象限内的任意一点，过点P作圆C的切线l，且l交x轴于点A，交y

 轴于点B，设，求的最小值(O为坐标原点).

19．(本小题满分16分)

设函数f(x)的定义域和值域均为，且对任意，都成等差数

列．又正项数列 其前n项和S_n满足

(1)求数列的通项公式；

(2)若的等比中项，求数列{b_n}前n项的和T_n.

20．(本小题满分16分)

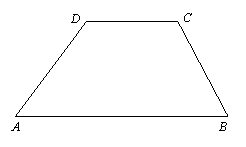
已知梯形ABCD, AB∥CD, AB=a, CD=b, a>b．现给出端点在两腰上、且与两底边平行的三条线

段PQ、RS、MN：①线段PQ是梯形的中位线；②线段RS将梯形的面积等分；③线段MN将梯

形分成相似的两个梯形．

(1)在图中大致作出三条线段PQ、RS、MN，并由此得出三条线段的大小关系是　▲　；

(2)证明你的结论；

(3)另有一条端点在两腰上、且与两底边平行的线段， 其

 长度为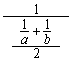，请你给出该线段的特征，并证明它

与(1)中的三条线段比较，长度最小.

高一数学参考答案及评分标准200807

一、填空题

1．(1，－2，3)　　　　　  2.　2　　　　　　　　   3. 　　　　　　　　4. 　

5.　①②　　　　　　 　　 6. 　　　　　　　　7. －10　　　　　　  8. 或

9.　0　　　　　　　　　  10. 外切　　　　　　　  11. 　　　　　　12.

13. 　　　　　　　　  14. 　 

二、解答题

15．(1)因为ABCD－A₁B₁C₁D₁是直四棱柱，所以，A₁C₁//AC，

而A₁C₁平面B₁AC，AC平面B₁AC，所以A₁C₁//平面B₁AC.　　　　　　　　 …………3分

同理，A₁D//平面B₁AC.　　　　 　　　　　　　　　　　　　　　　　　　　　…………5分

因为 A₁C₁、A₁D 平面DC₁A₁，A₁C₁A₁D ＝A₁，

所以平面B₁AC//平面DC₁A₁.　　　　　　　　　　　　　　　　　　　　　　   …………7分

(2) 因为ABCD－A₁B₁C₁D₁是直四棱柱，所以B₁B⊥平面ABCD，　　　　　  　…………9分

而AC平面ABCD，所以AC⊥B₁B.

因为底面ABCD是菱形，所以AC⊥BD.

因为B₁B、BD平面B₁BDD₁，B₁B BD＝B，所以AC⊥平面B₁BDD₁.　　　　…………12分

因为AC平面B₁AC，故有平面B₁AC⊥平面B₁BDD₁.　　　　　　　　 　　　…………14分

16．(1) 连结BD，因为，

所以，　　　　　　　　　　　　　　　　　  …………2分

在中,

，

于是.　　　　　 　　　　　　　　　　　　　　　　　　　　　　…………5分

因为，所以，

从而.　　　　　　　　　 …………7分

在中,

所以．　　 　　　　　　　　　　　…………10分

(2)因为

所以四边形ABCD的面积

S_ABCD=S_△DBC+ S_△DBA=50(9+) .　　　…………14分

17. 已知等差数列11，14，17，…的通项公式为.　　　　　 …………3分

(1)由，得，

又N^*, 所以该数列在[100，200]上有34项.　　　　　　　　　　　　　　　  …………6分

其和．　　　　　　　　　　　　　　　 …………9分

(2)因为，所以　　　　　　　　　　　　　　　　  …………11分

对任意的正整数n, ，且，

于是是首项和公比均为的等比数列.　　　　　　　　　　　　　　　　 …………13分

所以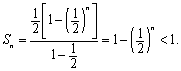　　　　　　　　　　　　　　　　　　　　…………15分

18．(1) 圆C：x²＋y²＝r²()的圆心为O(0，0)，于是

由题设知，是以D为直角顶点的直角三角形，

故有　　　　　　　　　　　　　　　　  …………5分

(2) 设P(x₀，y₀)()，则，

且直线l的方程为.　　　　　　　　　　　　　　　　　　　　　  …………7分

令y＝0，得x＝，即，

令x＝0，得y＝，即.

于是.　　　　　　　　　　　   …………10分

因为, 且，所以　　　　　　　　 …………12分

所以　　　  …………14分

当且仅当时取“＝”号.

故当时，取得最小值6.　　　　　　　　　　　　　　　  …………15分

19．(1)因为成等差数列，所以，

于是　　　　　　　　　  　　　　　　　　　　　　　　　…………2分

因为所以，

所以

故是以为公差的等差数列．　　　　　　　　　　　　　　　　　　  …………6分

因为，

所以　　　　　　　　　　　　　　　　　　　　　　　　　  …………8分

所以.　　　…………10分

(2)因为数列的等比中项，所以　　　　　　　 …………12分

于是　　　　　　　　　　　 …………14分

故　　　  …………16分

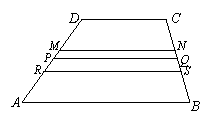20．(1)如图(只要求三条线段的顺序关系正确).　　…………2分

三条线段的大小关系是　MN<PQ<RS　；　　…………4分

(2)中位线PQ=.　　　　　　　　　　  …………5分

由于梯形ABNM与梯形MNCD相似，所以，即，　　　…………7分

设RS=x，梯形ABCD的高=h，

则梯形RSCD的高=，则，

解之，RS=，　　　　　　　　　　　　　　　　　　　　　　　　  …………9分

由基本不等式知；

又，所以<,

故MN<PQ<RS．　　　　　　　　　　　　　　　　　　　　　　　　　　　 …………12分

(3)设梯形ABCD的对角线AC与BD相交于点O，

则端点在两腰上、且与两底边平行并过点O的线段长为.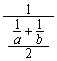　　　　　　

如图，设EF为上述线段，由三角形相似可得

，于是.

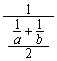同理可得，从而.　　　　　　　　　　　　  …………14分

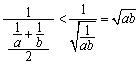因为，所以EF==MN，

而MN<PQ<RS，

故该线段与(1)中的三条线段比较，长度最小.　　　　　　　　　　　　　　　 …………16分