高一数学第二学期期末质量监测试卷
时量:120分钟 分值:150分 .适用学校:全市各高中.
范围:数学必修四(第二章)、数学必修五、必修二(不含圆方程).
注意:本次考试不得使用计算器.
一、选择题(本大题共12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案的代号填在答卷的相应表格内)
1.以下直线中,倾斜角是135°的是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.已知![]() ,则下列不等式中成立的是
,则下列不等式中成立的是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.若![]() ,则当
,则当![]() 时,
时,![]() 与
与![]() 垂直.
垂直.
A.-1 B.-2 C.1 D.2
4.不等式![]() 的解集是
的解集是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
5.已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,则
,则![]() 的值是
的值是
(A)12 (B)14 (C)16 (D)18
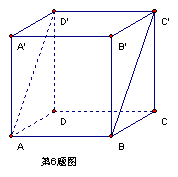
6.如图,在正方体![]() 中,二面角
中,二面角![]() 的大小是
的大小是
(A)30°(B)45°(C)60°(D)90°
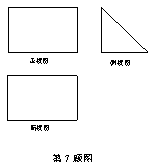 |
7.如图,一个空间几何体的正视图、俯视图都是长为3,宽为2的矩形,侧视图是腰长为2的等腰直角三角形,则它的表面积是
(A)14(B)![]() (C)
(C)![]() (D)16
(D)16
8.已知圆柱的体积是20pcm3,侧面积是40pcm2,那么它的高是
(A)24 cm (B)20cm (C)16cm (D)8cm
9.已知数列![]() 满足:
满足:![]() ,
,![]() .则
.则![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10.已知不重合的两直线![]() ,不重合的两平面
,不重合的两平面![]() ,下面命题中正确的是
,下面命题中正确的是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
11.某地区去年石油需求量为a,预计在今后5年内每年比上一年需求量增长12%,则从今年起到第五年,预计这个地区的总需求量为( )
(A)![]() (B)
(B)![]() (C)
(C)![]()
![]() (D)
(D)![]()
12.在平面直角坐标系内,一束光线从点A![]() 出发,被x轴反射后到达点B(2,7),则这束光线从A到B所经过的距离为
出发,被x轴反射后到达点B(2,7),则这束光线从A到B所经过的距离为
(A)12 (B)13
(C)![]() (D)
(D)![]()
二、填空题(本大题共6小题,每小题5分,共30分,请将正确答案填空在答卷上)
13.在△ABC中,已知![]() ,则C= (填角度)
,则C= (填角度)
14.已知:向量e1与e2的夹角为120°,e1= e2=1,则 e1+2 e2= .
15.(仅市三中做)过点A(3,4)和点B(-1,-4)的直线的方程是:_________________.
(非市三中做)点P(-3,5)到直线![]() 的距离是________.
的距离是________.
16.设![]() 满足约束条件:
满足约束条件: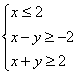 ,则
,则![]() 的最大值是__ _______.
的最大值是__ _______.
17.长方体共顶点的三个面的面积分别为12cm2,15cm2,20cm2,则它的外接球表面积为 .
18.不等式![]() 在区间
在区间![]() 上恒成立,则实数
上恒成立,则实数![]() 的范围是________.
的范围是________.
三、解答题(本大题共5小题,每小题12分,共60分.请将详细解答过程写在答卷上)
19.已知直线![]() :
:![]() ,
,![]() :
:![]() ,它们相交于点A.
,它们相交于点A.
(1)判断直线![]() 和
和![]() 是否垂直?请给出理由;
是否垂直?请给出理由;
(2)求过点A且与直线![]() :
:![]() 平行的直线方程(请给出一般式).
平行的直线方程(请给出一般式).
20.在三角形ABC中,BC=3cm,![]() .
.
(1)若A=![]() ,求AC;
,求AC;
(2)若三角形ABC的面积为![]() cm2,求AC.
cm2,求AC.
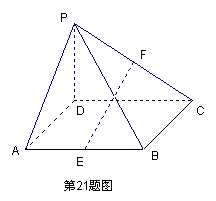 21.如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD,点E、F分别是AB和PC的中点.
21.如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD,点E、F分别是AB和PC的中点.
(1) 求证:AB⊥平面PAD;
(2) 求证:EF//平面PAD.
22.如图,从一个半径为R的半圆形铁片中截出一个矩形ABCD,设边AB的长为x.
(1) 试用x表示矩形的面积S;
(2)
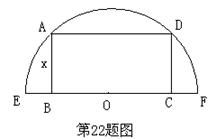 当S取最大值时,求x的值.
当S取最大值时,求x的值.
23.对任意正整数![]() ,数列
,数列![]() 均满足
均满足![]() .
.
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)求![]() 的通项
的通项![]() ;
;
(3)已知![]() ,求
,求![]() .
.
珠海市2007-2008学年度第二学期期末质量监测
高一数学参考答案及评分标准
时量:120分钟 分值:150分 .适用学校:全市各高中.
范围:数学必修四(第二章)、数学必修五、必修二(不含圆方程).
注意:本次考试不得使用计算器.
一、选择题(本大题共12小题,每小题5分,共60分。)
| 题目 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | D | D | A | B | B | C | B | C | D | C | B |
1.以下直线中,倾斜角是135°的是 C
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.已知![]() ,则下列不等式中成立的是 D
,则下列不等式中成立的是 D
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.若![]() ,则当
,则当![]() 时,
时,![]() 与
与![]() 垂直.D
垂直.D
A.-1 B.-2 C.1 D.2
4.不等式![]() 的解集是
A
的解集是
A
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
5.已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,则
,则![]() 的值是 B
的值是 B
(A)12 (B)14 (C)16 (D)18
6.如图,在正方体![]() 中,二面角
中,二面角![]() 的大小是 B
的大小是 B
(A)30°(B)45°(C)60°(D)90°
 |

7.如图,一个空间几何体的正视图、俯视图都是长为3,宽为2的矩形,侧视图是腰长为2的等腰直角三角形,则它的表面积是 C
(A)14(B)![]() (C)
(C)![]() (D)16
(D)16
8.已知圆柱的体积是20pcm3,侧面积是40pcm2,那么它的高是 B
(A)24 cm (B)20cm (C)16cm (D)8cm
9.已知数列![]() 满足:
满足:![]() ,
,![]() 。则
。则![]() C
C
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10.已知不重合的两直线![]() ,不重合的两平面
,不重合的两平面![]() ,下面命题中正确的是 D
,下面命题中正确的是 D
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
11.某地区去年石油需求量为a,预计在今后5年内每年比上一年需求量增长12%,则从今年起到第五年,预计这个地区的总需求量为( )C
(A)![]() (B)
(B)![]() (C)
(C)![]()
![]() (D)
(D)![]()
12.在平面直角坐标系内,一束光线从点A![]() 出发,被x轴反射后到达点B(2,7),则这束光线从A到B所经过的距离为 B
出发,被x轴反射后到达点B(2,7),则这束光线从A到B所经过的距离为 B
(A)12 (B)13
(C)![]() (D)
(D)![]()
二、填空题(本大题共6小题,每小题5分,共30分,请将正确答案填空在答卷上)
13.在△ABC中,已知![]() ,则C= (填角度)60°
,则C= (填角度)60°
14.已知:向量e1与e2的夹角为120°,e1= e2=1,则 e1+2 e2=
.![]()
15.(仅市三中做)过点A(3,4)和点B(-1,-4)的直线的方程是:_________________.
答案:![]() (或
(或![]() 等其它形式)
等其它形式)
(非市三中学生做)点P(-3,5)到直线![]() 的距离是________.34/5
的距离是________.34/5
16.设![]() 满足约束条件:
满足约束条件: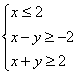 ,则
,则![]() 的最大值是__ _______.8
的最大值是__ _______.8
17.长方体共顶点的三个面的面积分别为12cm2,15cm2,20cm2,则它的外接球表面积为 .![]()
18.不等式![]() 在区间
在区间![]() 上恒成立,则实数
上恒成立,则实数![]() 的范围是________.
的范围是________.
![]() (或
(或![]() 或
或![]() )
)
三、解答题(本大题共5小题,每小题12分,共60分.请将详细解答过程写在答卷上)
19.已知直线![]() :
:![]() ,
,![]() :
:![]() ,它们相交于点A.
,它们相交于点A.
(1)判断直线![]() 和
和![]() 是否垂直?请给出理由;
是否垂直?请给出理由;
(2)求过点A且与直线![]() :
:![]() 平行的直线方程(请给出一般式).
平行的直线方程(请给出一般式).
解:(1)直线![]() 的斜率
的斜率![]() ,直线
,直线![]() 的斜率
的斜率![]() , (2分)
, (2分)
∵![]() (4分)
(4分)
∴![]() ⊥
⊥![]() (6分)
(6分)
(只写出结论给1分)
(2)由方程组![]() 解得点A坐标为
解得点A坐标为![]() ,(9分)
,(9分)
直线![]() 的斜率为-3,(10分)
的斜率为-3,(10分)
所求直线方程为:![]() (11分)
(11分)
化为一般式得:![]() (12分)
(12分)
20.在三角形ABC中,BC=3cm,![]() .
.
(1)若A=![]() ,求AC;
,求AC;
(2)若三角形ABC的面积为![]() cm2,求AC.
cm2,求AC.
解:(1)根据正弦定理,有![]() , (2分)
, (2分)
∴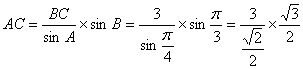 (5分)
(5分)
![]() (cm)(6分)
(cm)(6分)
(2)根据三角形面积公式,有![]() (7分)
(7分)
∴![]() (8分)
(8分)
即![]()
解得:![]() (cm) (9分)
(cm) (9分)
根据余弦定理:![]() (10分)
(10分)
∴![]() =13 (11分)
=13 (11分)
∴![]() (12分)
(12分)
 21.如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD,点E、F分别是AB和PC的中点.
21.如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD,点E、F分别是AB和PC的中点.
(3) 求证:AB⊥平面PAD;
(4) 求证:EF//平面PAD.
证明:(1)∵PD⊥平面ABCD,![]() ,
,
∴平面PDA⊥平面ABCD.(2分)
平面ABCD与平面PDA的交线为AD,(3分)
在矩形ABCD中,AD⊥AB(4分)
AB在平面ABCD内,(5分)
∴AB⊥平面PAD.(6分)
(2)取PD的中点G,连接FG,GA,(7分)
由G、F分别是PD、PC的中点,知GF是△PDC的中位线,
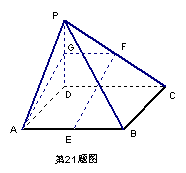 GF//DC,GF=
GF//DC,GF=![]() DC,(8分)
DC,(8分)
E是AB中点,AE=![]() AB,
AB,
矩形ABCD中,AB//DC,AB=DC,
∴GF//AE,GF=AE(9分)
∴四边形AEFG是平行四边形,EF//AG,(10分)
EF在平面PDA外,AG在平面PDA内,(11分)
∴EF//平面PDA.(12分)
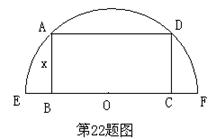 22.如图,从一个半径为R的半圆形铁片中截出一个矩形ABCD,设边AB的长为x.
22.如图,从一个半径为R的半圆形铁片中截出一个矩形ABCD,设边AB的长为x.
(3) 试用x表示矩形的面积S;
(4) 当S取最大值时,求x的值.
解:(1)连接AO,则AO=R,(2分)
在RT△ABO中,AB⊥BO,
BO=![]() ,(4分)
,(4分)
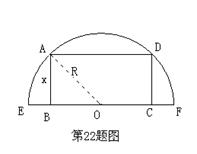 矩形ABCD的面积
矩形ABCD的面积![]() (7分)
(7分)
其中![]() (8分)
(8分)
(2)根据基本不等式:![]() ,(9分)
,(9分)
![]() (11分)
(11分)
当![]() 时,即
时,即![]() 时,S取得最大值.(12分)
时,S取得最大值.(12分)
(没有写出基本不等式,其它都正确,可以计满分)
23.对任意正整数![]() ,数列
,数列![]() 均满足
均满足![]() .
.
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)求![]() 的通项
的通项![]() ;
;
(3)已知![]() ,求
,求![]() .
.
解:(1)当![]() 时,可得:
时,可得:![]() ,(1分)
,(1分)
当![]() 时,可得
时,可得![]() ,∴
,∴![]() ,(2分)
,(2分)
当![]() 时,可得
时,可得![]() ,∴
,∴![]() (3分)
(3分)
(2)设![]() ,则由
,则由![]() 可得:
可得:
数列![]() 的前
的前![]() 项和
项和![]() ,(4分)
,(4分)
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]()
![]()
![]() (5分)
(5分)
∴![]()
∴![]() (6分)
(6分)
(3)由题意,得![]() ,(7分)
,(7分)
![]() (8分)
(8分)
![]() (10分)
(10分)
![]() (11分)
(11分)
![]() (12分)
(12分)
(以上仅为参考答案,如有不同解法,请参照此评分标准计分)