高中数学必修一第二章测试题(2)
一、选择题:
1.已知p>q>1,0<a<1,则下列各式中正确的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2、已知![]() ,则
,则![]() ( )
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3.函数![]() 当x>2 时恒有
当x>2 时恒有![]() >1,则a的取值范围是 ( )
>1,则a的取值范围是 ( )
A.![]() B.0
B.0![]() C.
C.![]() D.
D.![]()
4.北京市为成功举办2008年奥运会,决定从2003年到2007年五年间更新市内现有的全部出租车,若每年更新的车辆数比前一年递增10%,则2003年底更新现有总车辆数的(参考数据:1.14=1.46,1.15=1.61) ( )
A.10% B.16.4% C.16.8% D.20%
5. 设g(x)为R上不恒等于0的奇函数,![]() (a>0且a≠1)为偶函数,则常数b的值为 ( )
(a>0且a≠1)为偶函数,则常数b的值为 ( )
A.2
B.1 C.![]() D.与a有关的值
D.与a有关的值
6.当![]() 时,函数
时,函数![]() 和
和![]() 的图象只可能是 ( )
的图象只可能是 ( )

7、设![]() ,则
( )
,则
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
8.设f(x)=ax,g(x)=x![]() ,h(x)=logax,a满足loga(1-a2)>0,那么当x>1时必有 ( )
,h(x)=logax,a满足loga(1-a2)>0,那么当x>1时必有 ( )
A.h(x)<g(x)<f(x) B.h(x)<f(x)<g(x) C.f(x)<g(x)<h(x) D.f(x)<h(x)<g(x)
9、某商品价格前两年每年递增![]() ,后两年每年递减
,后两年每年递减![]() ,则四年后的价格与原来价格比较,变化的情况是( )
,则四年后的价格与原来价格比较,变化的情况是( )
A、减少![]() B、增加
B、增加![]() C、减少
C、减少![]() D、不增不减
D、不增不减
10. 对于幂函数![]() ,若
,若![]() ,则
,则![]() ,
,![]() 大小关系是( )
大小关系是( )
A.![]()
![]()
![]() B.
B. ![]()
![]()
![]()
C. ![]()
![]()
![]() D. 无法确定
D. 无法确定
二、填空题
11.已知函数f (x)的定义域是(1,2),则函数![]() 的定义域是
.
的定义域是
.
12.我国2000年底的人口总数为M,要实现到2010年底我国人口总数不超过N(其中M<N),则人口的年平均自然增长率p的最大值是 .
13.将函数![]() 的图象向左平移一个单位,得到图象C1,再将C1向上平移一个单位得到图象C2,作出C2关于直线y=x对称的图象C3,则C3的解析式为
.
的图象向左平移一个单位,得到图象C1,再将C1向上平移一个单位得到图象C2,作出C2关于直线y=x对称的图象C3,则C3的解析式为
.
14.已知-1<a<0,则三个数![]() 由小到大的顺序是
.
由小到大的顺序是
.
15.![]() 是偶函数,且在
是偶函数,且在![]() 是减函数,则整数
是减函数,则整数![]() 的值是
.
的值是
.
16.函数y=![]() 的单调递增区间是
.
的单调递增区间是
.
17.方程log2(2x+1)log2(2x+1+2)=2的解为
三、解答题:
18、判断函数![]() 的奇偶性单调性。
的奇偶性单调性。
19.已知函数![]() (a、b是常数且a>0,a≠1)在区间[-
(a、b是常数且a>0,a≠1)在区间[-![]() ,0]上有ymax=3,
,0]上有ymax=3,
ymin=![]() ,试求a和b的值.
,试求a和b的值.
20.已知函数f(x)=lg(a x2+2x+1)
(1)若f(x)的定义域是R,求实数a的取值范围及f(x)的值域;
(2)若f(x)的值域是R,求实数a的取值范围及f(x)的定义域.
21.(14分)某商品在近30天内每件的销售价格p(元)与时间t(天)的函数关系是![]() 该商品的日销售量Q(件)与时间t(天)的函数关系是
该商品的日销售量Q(件)与时间t(天)的函数关系是![]()
![]() ,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?
,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?
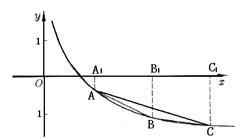
22.如图,A,B,C为函数![]() 的图象
的图象
|
(1)设![]() ABC的面积为S 求S=f (t) ;
ABC的面积为S 求S=f (t) ;
(2)判断函数S=f (t)的单调性;
(3) 求S=f (t)的最大值.
高中数学第二章测试题参考答案
BDABC ACBAA
11 (0,1); 12 ![]() -1
; 13
-1
; 13 ![]() ; 14
; 14 ![]() ;
;
15 5 ; 16 ![]() ; 17 0
; 17 0
18、奇函数,函数是减函数。
∵![]() ,
,![]()
∴![]()
即![]() ,∴函数
,∴函数![]() 是奇函数。
是奇函数。
设![]() ,设
,设![]() ,
,
则![]()
且![]()
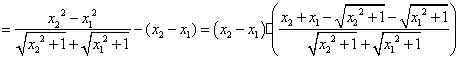
∵![]() ,∴
,∴![]()
∴![]() ,即
,即![]() ,∴函数
,∴函数![]() 在定义域内是减函数。
在定义域内是减函数。
19.解:令u=x2+2x=(x+1)2-1 x∈[-![]() ,0] ∴当x=-1时,umin=-1 当x=0时,umax=0
,0] ∴当x=-1时,umin=-1 当x=0时,umax=0

20.解:(1)因为f(x)的定义域为R,所以ax2+2x+1>0对一切x![]() R成立.
R成立.
由此得![]() 解得a>1. 又因为ax2+2x+1=a(x+
解得a>1. 又因为ax2+2x+1=a(x+![]() )+1-
)+1-![]() >0,
>0,
所以f(x)=lg(a x2+2x+1) ![]() lg(1-
lg(1-![]() ),所以实数a的取值范围是(1,+
),所以实数a的取值范围是(1,+ ![]() ) ,
) ,
f(x)的值域是![]()
( 2 ) 因为f(x)的值域是R,所以u=ax2+2x+1的值域![]() (0, +
(0, +![]() ).
).
当a=0时,u=2x+1的值域为R![]() (0, +
(0, +![]() );
);
当a≠0时,u=ax2+2x+1的值域![]() (0, +
(0, +![]() )等价于
)等价于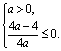
解之得0<a![]() 1. 所以实数a的取值范围是[0.1] 当a=0时,由2x+1>0得x>-
1. 所以实数a的取值范围是[0.1] 当a=0时,由2x+1>0得x>-![]() ,
,
f (x)的定义域是(-![]() ,+
,+![]() ); 当0<a
); 当0<a![]() 1时,由ax2+2x+1>0
1时,由ax2+2x+1>0
解得![]()
f (x)的定义域是![]() .
.
21.解:设日销售金额为y(元),则y=p![]() Q.
Q.
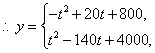
![]()
![]()
![]()
当![]() ,t=10时,
,t=10时,![]() (元);
(元);
当![]() ,t=25时,
,t=25时,![]() (元).
(元).
由1125>900,知ymax=1125(元),且第25天,日销售额最大.
22.解:(1)过A,B,C,分别作AA1,BB1,CC1垂直于x轴,垂足为A1,B1,C1,
则S=S梯形AA1B1B+S梯形BB1C1C-S梯形AA1C1C.
![]()
(2)因为v=![]() 在
在![]() 上是增函数,且v
上是增函数,且v![]() 5,
5,
![]() 上是减函数,且1<u
上是减函数,且1<u![]()
![]() ; S
; S![]() 上是增函数,
上是增函数,
所以复合函数S=f(t) ![]() 上是减函数
上是减函数
(3)由(2)知t=1时,S有最大值,最大值是f (1) ![]()