高一数学第二学期第二阶段考试试卷
（本卷满分160分，时间：120分钟）
一．填空题（本大题共14小题，每小题5分，共70分）
1．不等式
0的解集为： ▲ ．
2. 在等比数列{an}中 若a10＝6，a20＝3，则a30为： ▲ ．
3．在△ABC中, ∠B=120°,AB=2
,AC=6,则∠C为： ▲ ．
4．若a>1，则
的最小值是： ▲ ．
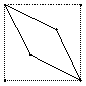
5．如右图所示的直观图，则其平面图形的面积为： ▲ ．
6. 在
中，已知
，则的形状是： ▲ ．
7．若△ABC的三边为a,b,c,它的面积为
，那么内角C等于： ▲ ．
8．已知直线
和平面
，下列推理错误的是： ▲ ．
①
且
②
∥
且 
③∥且∥
④且∥或
9．设
是等差数列
的前
项的和，若
，则
▲ ．
10．在正方体上任意选择4个顶点，它们可能是如下各种几何形体的4个顶点，这些几何形体是 ▲ ．（写出所有正确结论的编号）．
①矩形；
②不是矩形的平行四边形；
③有三个面为等腰直角三角形，有一个面为等边三角形的四面体；
④每个面都是等边三角形的四面体；
⑤每个面都是直角三角形的四面体.
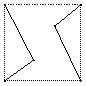
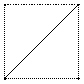
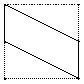
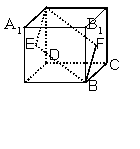
11．如图，E、F分别为正方体的面
，面
的中心，则四边形
在该正方体的面上的射影可能是： ▲ ．（填出所有可能的序号）
|
|
|
① ② ③ ④
12．已知函数
，数列满足：
且
（nÎN*），若数列
是等比数列，则常数c = ▲ ．
13．已知正数
满足
的最小值是9，则正数的值是： ▲ ．
14．将正整数按下表的规律排列，把行与列交叉处的一个数称为某行某列的数，记作aij (i,j
N*)，如第2行第4列的数是15，记作a24=15，则有序数对（a28，a84）是： ▲ ．
1 4 5 16 17 36 …
2 3 6 15 18 35 …
9 8 7 14 19 34 …
10 11 12 13 20 33 …
25 24 23 22 21 32 …
26 27 28 29 30 31 …
… … … … … … …
二．解答题（本大题共6小题，共90分）
|
，求AD与BC所成角的大小．
16．（本题14分）△ABC中，内角
的对边分别是
，满足成等比数列．
（１）求证：
；
（２）若
，求
的值．
17．（本题14分）已知等差数列
的前n项和为
，且
，
（１）求
的通项公式；
（２）设
，求证： 
是等比数列，并求数列
的前n项和
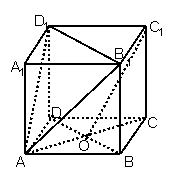
18．（本题16分）已知正方体
，
是底
对角线的交点.
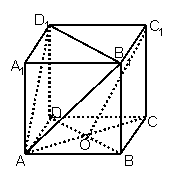求证：（１）
面
；
（2 ）
面．
19．（本题16分）
某人2006年年初投资98万元购买了一辆挖掘机，第一年各种费用12万元，以后每年费用都比上一年增加4万元，若每年挖掘收益为50万元．
（1） 问此人投资后第几年开始获利？
（2） 若年平均获利最大时，沟汰该挖掘机最合算，请问此人该使用到哪一年最合算？
20．（本题18分）
已知函数
满足
．
（Ⅰ）求
的值；
（Ⅱ）若数列
，求列数
的通项公式；
（Ⅲ）若数列
满足
，是数列前项的和，则当实数
大于
时，不等式
能否对于一切的
恒成立？
命题、校对：赵久勇
扬州市新华中学2007～2008学年度第二学期第二阶段考试
高一数学试卷答题纸
一．填空题
1._______________________________ 2._____________________________
3._______________________________ 4._____________________________
5._______________________________ 6._____________________________
7._______________________________ 8._____________________________
9._______________________________ 10._____________________________
11．_____________________________ 12._____________________________
13.______________________________ 14._____________________________
二．解答题
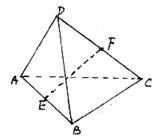15. （本题12分）
16．（本题14分）
17．（本题14分）
| 座位号 |
18．（本题16分）
19．（本题16分）
20．（本题18分）
高一数学第二学期第二阶段考试试卷答案
一、填空题：
1．
2． 
3．
4．3 5． 6
6．等腰三角形或直角三角形 7．
8．③ 9．1 10．1345 11．23 12．1 13．2 14．(63 ,53)
二、解答题
1５．（本题12分）
解：AD与BC所成角的大小为
---------------------------12分
16（本题14分）
解：（1）因为成等比数列，所以
． 又
．
∴
．
∵
，∴． ---------------------------6分
（2）∵，由正弦定理， 得
．
∵，∴
．
--------------------------10分
∵
而
， ∴
∴
． ---------------------------14分
17. （本题14分）
解：（1）由题意的
解得
所以
---------------------------4分
（2）证明：由第（1）问得
所以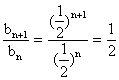
所以数列
是以
为首项，为公比的等比数列.
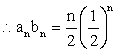---------------------------8分
①
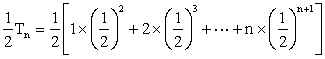②
①－②得：
---------------------------16分
18．（本题16分）
证明：（1）连结
，设
连结
，
是正方体
是平行四边形
且 
又
分别是
的中点，
且
是平行四边形
面
，
面
面
---------------------------８分
（2）
面
又
， 
同理可证
，
又
面
---------------------------16分
19.（本题满分16分）
解：（1）由题设知每年的费用是以12为首项，4为公差的等差数列．则纯收入y与年数n的关系为
y＝50n－[12＋16＋…＋(8＋4n)]－98＝40n－2n2－98．
由y>0得 40n－2n2－98>0
即 
又因为n∈N＋，所以3≤n≤17
答：从第三年开始获利． ---------------------------８分
(2) 由上题知，年平均获利为
＝40－2(n＋
)
∵n＋≥2
＝14，当仅且当n＝7时取等号
∴当仅且当n＝7时，有最大值12．
答：此人使用7年到2012年沟汰该机器最合算．---------------------------16分
20（本题16分）
（Ⅰ）令
，
，
，
令
，
---------------------------４分
（Ⅱ）∵
①
∴
②
由（Ⅰ），知
∴①+②，得
---------------------------10分
（Ⅲ）∵ ，∴ 
∴
，
①
， ②
①－②得
即
---------------------------14分不等式恒成立，即
对于一切的恒成立，
设
当
时，由于对称轴直线
，且 
，而函数
在
是增函数，∴不等式
恒成立
即当实数大于时，不等式能否对于一切的恒成立 ---------18分