等比数列·例题解析

等比数列·例题解析

 

【例1】　已知S_n是数列{a_n}的前n项和，S_n＝pⁿ(p∈R，n∈N*)，那么数列{a_n}．

[　　]

A．是等比数列

B．当p≠0时是等比数列

C．当p≠0，p≠1时是等比数列

D．不是等比数列

分析　由S_n＝pⁿ(n∈N*)，有a₁=S₁＝p，并且当n≥2时，

a_n=S_n－S_n-1＝pⁿ－p^n-1＝(p－1)p^n-1

但满足此条件的实数p是不存在的，故本题应选D．

说明　数列{a_n}成等比数列的必要条件是a_n≠0(n∈N*)，还要注

【例2】　已知等比数列1，x₁，x₂，…，x_2n，2，求x₁·x₂·x₃·…·x_2n．

解　∵1，x₁，x₂，…，x_2n，2成等比数列，公比q

∴2＝1·q²ⁿ⁺¹

x₁x₂x₃…x_2n＝q·q²·q³…q²ⁿ=q^1+2+3+…+2n

式；(2)已知a₃·a₄·a₅＝8，求a₂a₃a₄a₅a₆的值．

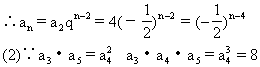
∴a₄＝2

【例4】　已知a＞0，b＞0且a≠b，在a，b之间插入n个正数x₁，x₂，…，x_n，使得a，x₁，x₂，…，x_n，b成等比数列，求

证明　设这n＋2个数所成数列的公比为q，则b=aqⁿ⁺¹

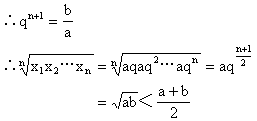
【例5】　 设a、b、c、d成等比数列，求证：(b－c)²＋(c－a)²＋(d－b)²＝(a－d)²．

证法一　∵a、b、c、d成等比数列

∴b²＝ac，c²＝bd，ad＝bc

∴左边=b²－2bc＋c²＋c²－2ac＋a²＋d²－2bd＋b²

=2(b²－ac)＋2(c²－bd)＋(a²－2bc＋d²)

＝a²－2ad＋d²

＝(a－d)²＝右边

证毕．

证法二　∵a、b、c、d成等比数列，设其公比为q，则：

b＝aq，c＝aq²，d=aq³

∴左边＝(aq－aq²)²＋(aq²－a)²＋(aq³－aq)²

＝a²－2a²q³＋a²q⁶

=(a－aq³)²

＝(a－d)²=右边

证毕．

说明　这是一个等比数列与代数式的恒等变形相综合的题目．证法一是抓住了求证式中右边没有b、c的特点，走的是利用等比的条件消去左边式中的b、c的路子．证法二则是把a、b、c、d统一化成等比数列的基本元素a、q去解决的．证法二稍微麻烦些，但它所用的统一成基本元素的方法，却较证法一的方法具有普遍性．

【例6】　求数列的通项公式：

(1){a_n}中，a₁＝2，a_n+1＝3a_n＋2

(2){a_n}中，a₁=2，a₂＝5，且a_n+2－3a_n+1＋2a_n＝0

思路：转化为等比数列．

∴{a_n＋1}是等比数列

∴a_n＋1=3·3^n-1　∴a_n=3ⁿ－1

∴{a_n+1－a_n}是等比数列，即

a_n+1－a_n=(a₂－a₁)·2^n-1=3·2^n-1

再注意到a₂－a₁=3，a₃－a₂=3·2¹，a₄－a₃=3·2²，…，a_n－a_n-1=3·2^n-2，这些等式相加，即可以得到

说明　解题的关键是发现一个等比数列，即化生疏为已知．(1)中发现{a_n＋1}是等比数列，(2)中发现{a_n+1－a_n}是等比数列，这也是通常说的化归思想的一种体现．

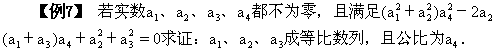
证　∵a₁、a₂、a₃、a₄均为不为零的实数

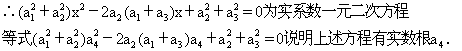
∴上述方程的判别式Δ≥0，即

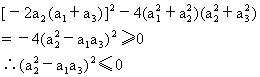
又∵a₁、a₂、a₃为实数

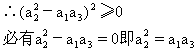
因而a₁、a₂、a₃成等比数列

∴a₄即为等比数列a₁、a₂、a₃的公比．

【例8】　若a、b、c成等差数列，且a＋1、b、c与a、b、c＋2都成等比数列，求b的值．

解　设a、b、c分别为b－d、b、b＋d，由已知b－d＋1、b、b＋d与b－d、b、b＋d＋2都成等比数列，有

整理，得

∴b＋d=2b－2d　即b=3d

代入①，得

9d²=(3d－d＋1)(3d＋d)

9d²=(2d＋1)·4d

解之，得d=4或d=0(舍)

∴b=12

【例9】　已知等差数列{a_n}的公差和等比数列{b_n}的公比都是d，又知d≠1，且a₄=b₄，a₁₀=b₁₀：

(1)求a₁与d的值；

(2)b₁₆是不是{a_n}中的项？

思路：运用通项公式列方程

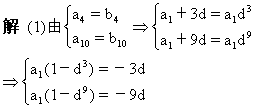
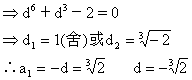
(2)∵b₁₆=b₁·d¹⁵=－32b₁

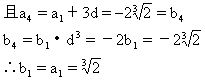
∴b₁₆=－32b₁=－32a₁，如果b₁₆是{a_n}中的第k项，则

－32a₁=a₁＋(k－1)d

∴(k－1)d=－33a₁=33d

∴k=34即b₁₆是{a_n}中的第34项．

解　设等差数列{a_n}的公差为d，则a_n=a₁＋(n－1)d

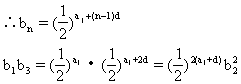
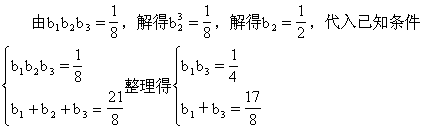
解这个方程组，得

∴a₁=－1，d=2或a₁=3，d=－2

∴当a₁=－1，d=2时，a_n=a₁＋(n－1)d=2n－3

当a₁=3，d=2时，a_n=a₁＋(n－1)d=5－2n

【例11】　三个数成等比数列，若第二个数加4就成等差数列，再把这个等差数列的第3项加32又成等比数列，求这三个数．

解法一　按等比数列设三个数，设原数列为a，aq，aq²

由已知：a，aq＋4，aq²成等差数列

即：2(aq＋4)=a＋aq²①

a，aq＋4，aq²＋32成等比数列

即：(aq＋4)²=a(aq²＋32)

解法二　按等差数列设三个数，设原数列为b－d，b－4，b＋d

由已知：三个数成等比数列

即：(b－4)²=(b－d)(b＋d)

b－d，b，b＋d＋32成等比数列

即b²=(b－d)(b＋d＋32)

解法三　任意设三个未知数，设原数列为a₁，a₂，a₃

由已知：a₁，a₂，a₃成等比数列

a₁，a₂＋4，a₃成等差数列

得：2(a₂＋4)=a₁＋a₃②

a₁，a₂＋4，a₃＋32成等比数列

得：(a₂＋4)²=a₁(a₃＋32)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　③

说明　将三个成等差数列的数设为a－d，a，a＋d；将三个成

简化计算过程的作用．

【例12】　有四个数，其中前三个数成等差数列，后三个数成等比数列，并且第一个数与第四个数的和是16，第二个数与第三个数的和是12，求这四个数．

分析　本题有三种设未知数的方法

方法一　设前三个数为a－d，a，a＋d，则第四个数由已知条

方法二　设后三个数为b，bq，bq²，则第一个数由已知条件推得为2b－bq．

方法三　设第一个数与第二个数分别为x，y，则第三、第四个数依次为12－y，16－x．

由这三种设法可利用余下的条件列方程组解出相关的未知数，从而解出所求的四个数，

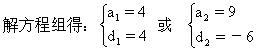
所求四个数为：0，4，8，16或15，9，3，1．

解法二　设后三个数为：b，bq，bq²，则第一个数为：2b－bq

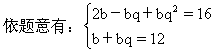
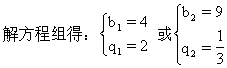
所求四个数为：0，4，8，16或15，9，3，1．

解法三　设四个数依次为x，y，12－y，16－x．

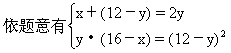
这四个数为0，4，8，16或15，9，3，1．

【例13】　已知三个数成等差数列，其和为126；另外三个数成等比数列，把两个数列的对应项依次相加，分别得到85，76，84．求这两个数列．

解　设成等差数列的三个数为b－d，b，b＋d，由已知，b－d＋b＋b＋d=126

∴b=42

这三个数可写成42－d，42，42＋d．

再设另三个数为a，aq，aq²．由题设，得

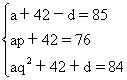
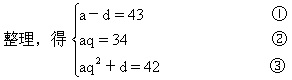
解这个方程组，得

a₁=17或a₂=68

当a=17时，q=2，d=－26

从而得到：成等比数列的三个数为17，34，68，此时成等差的三个数为68，42，16；或者成等比的三个数为68，34，17，此时成等差的三个数为17，42，67．

【例14】　已知在数列{a_n}中，a₁、a₂、a₃成等差数列，a₂、a₃、a₄成等比数列，a₃、a₄、a₅的倒数成等差数列，证明：a₁、a₃、a₅成等比数列．

证明　由已知，有

2a₂=a₁＋a₃　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　①

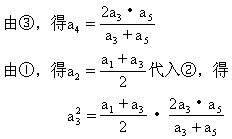
即　a₃(a₃＋a₅)=a₅(a₁＋a₃)

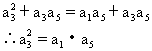
所以a₁、a₃、a₅成等比数列．

【例15】　已知(b－c)log_mx＋(c－a)log_my＋(a－b)log_mz=0．

(1)设a，b，c依次成等差数列，且公差不为零，求证：x，y，z成等比数列．

(2)设正数x，y，z依次成等比数列，且公比不为1，求证：a，b，c成等差数列．

证明　(1)∵a，b，c成等差数列，且公差d≠0

∴b－c=a－b=－d，c－a=2d

代入已知条件，得：－d(log_mx－2log_my＋log_mz)=0

∴log_mx＋log_mz=2log_my

∴y²=xz

∵x，y，z均为正数

∴x，y，z成等比数列

(2)∵x，y，z成等比数列且公比q≠1

∴y=xq，z=xq²代入已知条件得：

(b－c)log_mx＋(c－a)log_mxq＋(a－b)log_mxq²=0

变形、整理得：(c＋a－2b)log_mq=0

∵q≠1　∴log_mq≠0

∴c＋a－2b=0　即2b=a＋c

即a，b，c成等差数列