双曲线解答题4
61、双曲线16x2-9y2
= 144,F1、F2是左、右焦点,P在双曲线上,且![]() ,求
,求![]() F1PF2的大小。
F1PF2的大小。
翰林汇62、已知双曲线的中心在原点,以坐标轴为对称轴,且与圆x2+y2 = 17相交于点A(4,-1),若此圆在A点之切线与双曲线一条渐近线平行,求此双曲线方程。翰林汇
63、直线y = ax+1和双曲线3x2-y2 =1相交,交点为A,B,当a为何值时,以AB为直径的圆经过坐标原点?翰林汇
64、点P(8,1)平分双曲线x2-4y2 = 4的一条弦,求这条弦所在的直线方程。翰林汇
65、经过双曲线![]() 的右焦点F2作倾斜角为300的弦AB,求:(1)AB;(2)
的右焦点F2作倾斜角为300的弦AB,求:(1)AB;(2)![]() F1AB的周长(F1是双曲线的左焦点)。翰林汇
F1AB的周长(F1是双曲线的左焦点)。翰林汇
66、求一条渐近线方程是3x+4y = 0,一个焦点是(4,0)的双曲线标准方程.
翰林汇67、求与双曲线![]() 有共同的渐近线,并且经过点(-3,2
有共同的渐近线,并且经过点(-3,2![]() )的双曲线方程。翰林汇
)的双曲线方程。翰林汇
68、当![]() 从00到1800变化时,曲线x2+y2cos
从00到1800变化时,曲线x2+y2cos![]() =1怎样变化?翰林汇
=1怎样变化?翰林汇
69、直线y=x+b与双曲线2x2-y2=2相交于A、B两点,若以AB为直径的圆经过原点,求b的值。
翰林汇70、给定双曲线![]() ,过点B(1,1)作直线m交双曲线于Q1、Q2两点,且B为Q1Q2的中点,这样的直线m是否存在?如果存在,求出它的方程;如果不存在,说明理由。翰林汇
,过点B(1,1)作直线m交双曲线于Q1、Q2两点,且B为Q1Q2的中点,这样的直线m是否存在?如果存在,求出它的方程;如果不存在,说明理由。翰林汇
71、设双曲线![]() 上有一点P,F1、F2为双曲线的两个焦点,且
上有一点P,F1、F2为双曲线的两个焦点,且![]() ,求三角形F1PF2的面积。
,求三角形F1PF2的面积。
翰林汇72、求两条渐近线为x+2y=0和x-2y=0,且截直线x-y-3=0所得弦长为![]() 的双曲线方程。翰林汇
的双曲线方程。翰林汇
73、已知圆O:x2+y2=1和双曲线E:x2-y2=1,直线l:y=kx+b交这两条曲线于不同的点A、B、C、D,设AB=CD,求k、b应满足什么条件?
翰林汇74、已知双曲线的离心率e=2,准线方程是2x+y=0,相应焦点为F(1,0),求双曲线的方程。
翰林汇75、双曲线![]() 的右支上一点P到左焦点F1与到右焦点F2的距离之比为
的右支上一点P到左焦点F1与到右焦点F2的距离之比为
m:n,求点P的横坐标。
翰林汇76、等轴双曲线的中心在原点,焦点在x轴上,与直线x-2y=0交于A、B两点,且AB=![]() ,求等轴双曲线的方程。
,求等轴双曲线的方程。
翰林汇77、求以椭圆![]() 的焦点为焦点,以直线
的焦点为焦点,以直线![]() 为渐近线的双曲线方程。翰林汇
为渐近线的双曲线方程。翰林汇
78、经过A(3,-1)作一条直线,使它被双曲线![]() 所截得的线段恰被A所平分,求这条直线的方程。翰林汇
所截得的线段恰被A所平分,求这条直线的方程。翰林汇
79、过双曲线![]() 的右焦点F作倾斜角为450的弦AB,求弦AB的中点C到焦点F的距离。
的右焦点F作倾斜角为450的弦AB,求弦AB的中点C到焦点F的距离。
翰林汇
双曲线解答题4 〈答卷〉
61、 ![]()
![]()
-![]() ∴1-cos
∴1-cos![]() = 1,
= 1,![]() .
.
翰林汇
62、 切线方程为4x-y =
17,渐近线方程为4x![]() y = 0,设双曲线方程为16x2-y2 =
y = 0,设双曲线方程为16x2-y2 = ![]() 点A坐标代入得
点A坐标代入得![]() ,∴所求双曲线方程为16x2-y2 = 255 .
,∴所求双曲线方程为16x2-y2 = 255 .
翰林汇
63、 y = ax+1代入3x2-y2 = 1得(3-a2)x2-2ax-2 =
0.![]() >0得
>0得![]() ,设A(x1,y1),B(x2,y2),∵OA
,设A(x1,y1),B(x2,y2),∵OA![]() OB,∴
OB,∴![]() 即x1x2+y1y2
= 0,∴x1x2+a2x1x2+a(x1+x2)+1 =
0得
即x1x2+y1y2
= 0,∴x1x2+a2x1x2+a(x1+x2)+1 =
0得![]() ,得a2 = 1,a =
,得a2 = 1,a = ![]() 满足
满足![]() ,
,
∴a=![]() 为所求。
为所求。
翰林汇
64、 解:设弦AB,A(x1,y1),B(x2,y2),
则 x12-4y12 = 4 (1)
x22-4y22 = 4 (2)
(1)-(2)得 (x1+x2)(x1-x2)-4(y1+y2)(y1-y2) = 0.
∵x1+x2 = 16,y1+y2 = 2
代入,得 ![]()
∴弦所在直线方程为y-1 = 2(x-8),即2x-y-15 = 0.
翰林汇
65、 解:(1)3;(2)![]() 翰林汇
翰林汇
66、 解:由3x+4y=0![]() ,因为一个焦点在x轴上,故设所求的双曲线的标准
,因为一个焦点在x轴上,故设所求的双曲线的标准
方程为![]() ,得c2 = a2+b2
=
,得c2 = a2+b2
= ![]() ∵c =
4 ∴
∵c =
4 ∴![]()
故所求双曲线的标准方程为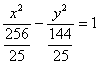 .
.
翰林汇67、 解:设所求双曲线方程为![]()
∵经过点(-3,2![]() ),∴
),∴![]() .
.
故所求双曲线方程为![]() ,即16x2-9y2 = 36.翰林汇
,即16x2-9y2 = 36.翰林汇
68、 ![]() =00时,圆x2+y2=1;00<
=00时,圆x2+y2=1;00<![]() <900时,椭圆x2+
<900时,椭圆x2+![]() =1;
=1;
![]() =900时,两条直线x=
=900时,两条直线x=![]() ;900<
;900<![]() <1800时,双曲线x2-
<1800时,双曲线x2-![]() =1;
=1;
![]() =1800时等轴双曲线x2-y2=1
=1800时等轴双曲线x2-y2=1
翰林汇
69、 ![]() 翰林汇
70、 不存在翰林汇 71、
翰林汇
70、 不存在翰林汇 71、 ![]() 翰林汇
翰林汇
72、 ![]() 翰林汇 73、 k=0时0<b2<1或b=0时0<k2<1翰林汇
翰林汇 73、 k=0时0<b2<1或b=0时0<k2<1翰林汇
74、 11x2+16xy-y2+10x-5=0翰林汇 75、 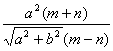 翰林汇
翰林汇
76、 x2-y2=9翰林汇 77、 ![]() 翰林汇 78、 3x+4y-5=0
翰林汇 78、 3x+4y-5=0
翰林汇79、 ![]()
翰林汇