高二数学期末复习一（不等式2）
一、选择题
1.若a、b、c为实数，则下列命题正确的是( )
A.若a＞b，则ac2＞bc2 B.若a＜b＜0，则a2＞ab＞b2
C.若a＜b＜0，则
＜
D.若a＜b＜0，则
＞
2.若<<0,则下列不等式:①a+b<ab；②a>b；③a<b；④+>2.正确的不等式有( )
A.1个 B.2个 C.3个 D.4个
3.若a＞b＞1,P=
,Q=
(lga+lgb),R=lg(
),则( )
A.R＜P＜Q B.P＜Q＜R C.Q＜P＜R D.P＜R＜Q
4.角x,y满足－
＜x＜y＜,则x－y的取值范围是( )
A.(－π,0) B.(－π,π) C.(－,0) D.(－,)
5.下列命题中，真命题有( )
①若a+b＞0且ab＞0,则a＞0且b＞0 ②若a＞b且ab＞0,则a＞b＞0
③若＞
ad＞bc
④a＞b是
＞
成立的必要条件
A.①③ B.②③ C.②④ D.①④
6.两次购买同一种物品,可以有两种不同的策略.第一种是不考虑物品价格的升降,每次购买这种物品的数量一定；第二种是不考虑物品价格的升降,每次购买这种物品所花的钱数一定.若两次购买这种物品时价格不相同,则两种策略中比较经济的情况为( )
A.第一种策略经济 B.第二种策略经济 C.两种策略同样经济 D.不能判断
7.函数f(x)=x+
+3在(－∞，－2]上( )
A.无最大值，有最小值7 B.无最大值，有最小值－1
C.有最大值7，有最小值－1 D.有最大值－1，无最小值
8.一批救灾物资随26辆汽车从某市以v km/h速度匀速直达灾区，已知两地公路线长 400 km，为了安全起见，两辆汽车的间距不得小于(
)2 km，那么这批物资全部到达灾区，最少需要( )
9.已知h＞0，设甲:两实数a、b满足a－b＜2h；乙:两实数a、b满足a－1＜h且b－1＜h,则( )
A.甲是乙的充分但不必要条件 B.甲是乙的必要但不充分条件
C.甲是乙的充要条件 D.甲既不是乙的充分条件，也不是乙的必要条件
10.若x＞0,y＞0且
≤a·(
+
)成立，则a的最小值是( )
A.
B.
C.2 D.2
二、填空题
11.设0＜x＜1，则a=2,b=1+x,c=
中最大的一个是__________.
12.已知不等式:①a2+3＞2a(a∈R)；②
≥2；③a5+b5＞a3b2+a2b3；④a2+b2≥2(a－b－1)
(a,b∈R).其中正确的不等式的序号是__________.
13. b g糖水中有a g糖(b>a>0),若再添上m g糖(m>0),则糖水就变甜了.试根据这个事实,提炼一个不等式:__________.
14.已知三个不等式:①ab＞0；②－
＜－
；③bc＜ad.以其中两个作为条件，余下一个作为结论，则可以组成__________个正确的命题.
三、解答题
15设x、y、z∈R,比较5x2+y2+z2与2xy+4x+2z－2的大小.
16.比较下列两个数的大小:
(1) －1与2－
； (2)2－与
－
；
(3)从以上两小题的结论中，你能否得出更一般的结论？并加以证明.
17求证:
≥
(a＞0,b＞0).
18某单位决定投资3200元建一仓库(长方体状)，高度恒定，它的后墙利用旧墙不花钱，正面用铁栅，每米长造价40元，两侧墙砌砖，每米造价45元，顶部每平方米造价20元，试算:仓库底面积S的最大允许值是多少？此时铁栅长为多少？
19.设f(x)=x2－x+B,实数a满足x－a＜1,求证:f(x)－f(a)＜2(a+1).
20 经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度v(km/h)之间的函数关系为y=
(v>0).
(1)在该时段内,当汽车的平均速度v为多少时,车流量最大?最大车流量为多少?(精确到0.1千辆/小时)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
21.已知a>b>0,求证:
<－
<
不等式(一)(A卷)
一、选择题
1.若a、b、c为实数，则下列命题正确的是( )
A.若a＞b，则ac2＞bc2 B.若a＜b＜0，则a2＞ab＞b2
C.若a＜b＜0，则＜ D.若a＜b＜0，则＞
解析:A.因为c2≥0,所以只有c≠0时才正确.c=0时，ac2=bc2，所以A是假命题.
变式:若ac2＞bc2,则a＞b，命题是真命题.
B.a＜b,a＜0a2＞ab,a＜b,b＜0ab＞b2，B是真命题.
C.由性质定理a＜b＜0＞,C是假命题.
D.例如－3＜－2＜0,
＜
,D是假命题.
答案:B
2.若<<0,则下列不等式:①a+b<ab；②a>b；③a<b；④+>2.正确的不等式有( )
A.1个 B.2个 C.3个 D.4个
分析:本题主要考查不等式的性质及均值不等式的适用条件.
解:由<<0可知b<a<0,③不正确,②不正确.
∴a+b<0,ab>0.∴a+b<ab,①正确.
由>0, >0,而a≠b,∴+>2,④正确.
答案:B
3.若a＞b＞1,P=,Q=(lga+lgb),R=lg(),则( )
A.R＜P＜Q B.P＜Q＜R C.Q＜P＜R D.P＜R＜Q
分析:本题主要考查均值不等式与对数函数的单调性.
解:a＞b＞1lga＞0,lgb＞0.
R＞Q＞P.
答案:B
4.角x,y满足－＜x＜y＜,则x－y的取值范围是( )
A.(－π,0) B.(－π,π) C.(－,0) D.(－,)
分析:本题主要考查负数在不等式中的变化，不等式的性质.
解:由x＜y，得x－y＜0.又－π＜x－y＜π，
∴－π＜x－y＜0.
答案:A
5.下列命题中，真命题有( )
①若a+b＞0且ab＞0,则a＞0且b＞0 ②若a＞b且ab＞0,则a＞b＞0
③若＞ad＞bc
④a＞b是＞成立的必要条件
A.①③ B.②③ C.②④ D.①④
分析:本题主要考查不等式的性质，用排除法.
解:∵ab＞0,∴a、b同号.又a+b＞0,
∴a＞0且b＞0.①正确，排除B、C.
由③－＞0，得
＞0，不能保证ad＞bc.③不正确.故应选D.
答案:D
6.两次购买同一种物品,可以有两种不同的策略.第一种是不考虑物品价格的升降,每次购买这种物品的数量一定；第二种是不考虑物品价格的升降,每次购买这种物品所花的钱数一定.若两次购买这种物品时价格不相同,则两种策略中比较经济的情况为( )
A.第一种策略经济 B.第二种策略经济 C.两种策略同样经济 D.不能判断
分析:本题主要考查不等式的应用.本题关键是比较两种不同的购买方式的平均价格的 大小.
解:(1)按第一种策略购物,设第一次购物时价格为p1,购n(kg),第二次购物时价格为p2,仍购n(kg).按这种策略购物时两次购物的平均价格为
=
.
(2)若按第二种策略购物,第一次花m元钱,能购
(kg)物品,第二次仍花m元钱,能购
(kg)物品,两次购物的平均价格为
=
.
比较两次购物的平均价格－
=－
=
=
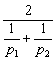>0(∵p1≠p2),
∴第一种策略的平均价格高于第二种策略的平均价格.
因而,用第二种策略比较经济.
答案:B
7.函数f(x)=x++3在(－∞，－2]上( )
A.无最大值，有最小值7 B.无最大值，有最小值－1
C.有最大值7，有最小值－1 D.有最大值－1，无最小值
解析:f(x)=x++3=－(－x+
)+3≤－4+3=－1.
故选D.
答案:D
8.一批救灾物资随26辆汽车从某市以v km/h速度匀速直达灾区，已知两地公路线长 400 km，为了安全起见，两辆汽车的间距不得小于()2 km，那么这批物资全部到达灾区，最少需要( )
A.5 h B.10 h C.15 h D.20 h
解析:时间t=［400+25()2］÷v=
+
≥2
=10.
答案:B
9.已知h＞0，设甲:两实数a、b满足a－b＜2h；乙:两实数a、b满足a－1＜h且b－1＜h,则( )
A.甲是乙的充分但不必要条件 B.甲是乙的必要但不充分条件
C.甲是乙的充要条件 D.甲既不是乙的充分条件，也不是乙的必要条件
分析:本题主要考查含绝对值不等式a－b≤a±b≤a+b，充要条件.
解:a－b=(a－1)－(b－1)≤a－1+b－1＜2h.故应选B.
答案:B
10.若x＞0,y＞0且≤a·(+)成立，则a的最小值是( )
A. B. C.2 D.2
分析:本题主要考查
≥()2,参数隔离法.
解:由
≥(
)2，
∴
≥,即a≥,amin=.故应选A.
答案:A
二、填空题
11.设0＜x＜1，则a=2,b=1+x,c=中最大的一个是__________.
解析:∵b－c=(1+x)－=
=－
＜0，
∴b＜c.又b=1+x＞2=a,∴c最大.
答案:c
12.已知不等式:①a2+3＞2a(a∈R)；②≥2；③a5+b5＞a3b2+a2b3；④a2+b2≥2(a－b－1)
(a,b∈R).其中正确的不等式的序号是__________.
分析:本题考查比较法，综合法证明不等式，凑平方.
解:①a2+3－2a=(a－1)2+2＞0.
②a为负值不正确.
③a5+b5－a3b2－a2b3=a3(a2－b2)－b3(a2－b2)=(a3－b3)(a2－b2)=(a+b)(a－b)2(a2+ab+b2)，其值大于零不一定成立.当a≠b且均为负值或一负值一零值时，其值为负值，当a=b时其值为零.不正确.
④a2+b2－2a+2b+2=(a－1)2+(b+1)2≥0.
答案:①④
13. b g糖水中有a g糖(b>a>0),若再添上m g糖(m>0),则糖水就变甜了.试根据这个事实,提炼一个不等式:__________.
分析:本题主要考查应用数学知识解决实际问题的能力.加糖以后,糖水变甜了,说明浓度变大了.
解:加糖以前,糖水的浓度为,而加入m g糖以后,糖水浓度为
,糖水变甜了,说明浓度变大了,即>.
答案: >
14.已知三个不等式:①ab＞0；②－＜－；③bc＜ad.以其中两个作为条件，余下一个作为结论，则可以组成__________个正确的命题.
分析:本题考查综合运用不等式的性质，证明不等式.
解:由②，
＞0,又ab＞0bc－ad＞0，
即bc＞ad，说明由①②
③.同理可证明其他情况.
答案:0
三、解答题
15设x、y、z∈R,比较5x2+y2+z2与2xy+4x+2z－2的大小.
分析:本题考查不等式的性质与比较法.
解:(5x2+y2+z2)－(2xy+4x+2z－2)=(x－y)2+(2x－1)2+(z－1)2≥0.
∴5x2+y2+z2≥2xy+4x+2z－2
(当且仅当x=y=且z=1时等号成立).
16.比较下列两个数的大小:
(1) －1与2－； (2)2－与－；
(3)从以上两小题的结论中，你能否得出更一般的结论？并加以证明.
解法一:(变形后利用平方求差)
(1)( +)2－(2+1)2=2－4＞0.
故+＞2+1，即－1＞2－.
(2)(2+)2－(+)2=4－2
=2
－2＞0.
故2+＞+ ,即2－＞－.
(3)一般结论:若n是正整数，
则有
－
＞
－
.
证明过程与(1)(2)类似，从略.
解法二:(利用分子有理化)
(1)∵－1=
,2－=
，而＞，故－1＞2－.
(2)∵2－=, －=
，
而＞,故2－＞－.
(3)同解法一.
注:本题的结论可推广到对一切n∈R+都成立.
17求证:≥(a＞0,b＞0).
思路一:从结论入手，探求、分析上一步成立的充分条件.
证法一:(分析法)要证≥，
只要证a
+b
≥a+b，
即证
+
≥().
需证()(a－+b)≥()，
即a－+b≥，
也就是要证a+b≥2成立.a+b≥2显然成立，∴原不等式成立.
思路二:从条件入手，利用已知不等式，逐次推理.
证法二:(综合法)∵a、b为正实数，∴a+b≥2.
又
+≥2, ①
+
≥2， ②
①+②得+++≥2+2，
即≥成立.
证法三:(作差比较法)
()－()
=(－)+(－)=
+
=
=
.
∵a、b为正实数，
∴＞0,＞0,(－)2≥0.
于是有≥0.
∴≥.
18某单位决定投资3200元建一仓库(长方体状)，高度恒定，它的后墙利用旧墙不花钱，正面用铁栅，每米长造价40元，两侧墙砌砖，每米造价45元，顶部每平方米造价20元，试算:仓库底面积S的最大允许值是多少？此时铁栅长为多少？
分析:本题考查不等式在实际中的应用.
解:设铁栅长x m，一堵墙长y m，则有S=xy.
由题意得40x+2×45y+20xy=3200.
应用二元均值不等式，得3200≥2
+20xy=120
+20xy=120
+20S.
∴S+6≤160.
∴(－10)(+16)≤0.
由于+16＞0,∴－10≤0，即S≤100.
因此S的最大允许值是100 m2，当且仅当40x=90y,
而xy=100,解得x=15，
即铁栅的长应为15 m.
19.设f(x)=x2－x+B,实数a满足x－a＜1,求证:f(x)－f(a)＜2(a+1).
分析:本题考查绝对值不等式a－b≤a±b≤a+b的应用.
证明:∵f(x)－f(a)=x2－x+B－a2+a－B=x2－a2－(x－a)=(x－a)(x+a－1)，
又∵x－a＜1,
∴f(x)－f(a)=x－a·x+a－1＜x+a－1
=x－a+2a－1≤x－a+2a－1＜1+2a+1=2(a+1).
∴f(x)－f(a)＜2(a+1).
20 经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度v(km/h)之间的函数关系为y=(v>0).
(1)在该时段内,当汽车的平均速度v为多少时,车流量最大?最大车流量为多少?(精确到0.1千辆/小时)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
分析:本题主要考查函数、不等式等基本知识,考查应用数学知识分析问题和解决问题的能力.
解:(1)依题意,y=
≤
=
,
当且仅当v=
,即v=40时,上式等号成立.
所以ymax=≈11.1(千辆/小时).
(2)由条件得>10,
整理得v2－89v+1600<0,
即(v－25)(v－64)<0.
解得25<v<64.
答:当v=40 km/h时,车流量最大,最大车流量约为11.1千辆/小时.如果要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应大于25 km/h且小于64 km/h.
21已知a>b>0,求证:<－<.
分析:本题主要考查利用分析法证明不等式.
证明:要证原不等式,只需证
<a+b－2<
(
)2<(－)2<(
)2
<－<
<1<
1+
<2<
+1
<1<
<1<. (*)
由题设知不等式(*)成立,以上过程可逆,原不等式成立.