广东肇庆实验中学2005—2006第一学期12月考试试卷
高二数学(文科)
一、选择题(每小题5分,共50分,请将正确答案填写到题后的答题卡上)
1.不等式“a+b>2c”成立的一个充分条件是(**)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2. 命题![]() .下列结论正确的是(**)
.下列结论正确的是(**)
A. ![]() 为真
B.
为真
B. ![]() 为真 C.
为真 C. ![]() 为假 D.
为假 D. ![]() 为真
为真
3.在⊿ABC中,A=45°,B=60°,a=10,则b等于( ** ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4.已知![]() ,则
,则![]() 有(**)
有(**)
A.最大值![]() B.最小值
B.最小值![]() C.最大值
C.最大值![]() D.最小值
D.最小值![]()
5. 椭圆![]() (a>b>0)的中心O与一个焦点F及短轴的一个端点M组成等腰直角三角形FMO,则它的离心率是( ** )
(a>b>0)的中心O与一个焦点F及短轴的一个端点M组成等腰直角三角形FMO,则它的离心率是( ** )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.如果数列![]() 的前
的前![]() 项和为
项和为![]() ,那么数列
,那么数列![]() 是(**)
是(**)
A.等差数列 B.等比数列
C.从第二项开始,以后各项成等差数列 D.从第二项开始,以后各项成等比数列.
7.若等比数列![]() 前n项和为Sn,且S1=18,S2=24,则S4=(**)
前n项和为Sn,且S1=18,S2=24,则S4=(**)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.与双曲线![]() 有共同的渐近线,且过点(2,2)的双曲线方程为(**)
有共同的渐近线,且过点(2,2)的双曲线方程为(**)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.已知:点(—2,3)与抛物线![]() 的焦点的距离是5,则
的焦点的距离是5,则![]() 的值是(**)
的值是(**)
A.2 B.4 C.8 D.16
10. 已知f(x)=(x-a)(x-b)-2,(a<b)并且![]() (
(![]() )是方程f(x)=0的两根,
)是方程f(x)=0的两根,
实数a、b、![]() 、
、![]() 的大小关系可能是 (** )
的大小关系可能是 (** )
A.a<![]() <
<![]() <b B.
<b B.
![]() <a<b<
<a<b<![]()
C.a<![]() <b<
<b<![]() D.
D.![]() <a<
<a<![]() <b
<b
二、填空题(每小题5分,共20分)
11. 曲线![]() 在点(1,1)处的切线方程为 ****** .
在点(1,1)处的切线方程为 ****** .
 12. 给出平面区域(如图),若使目标函数:z=ax+y(a>0)取得最大值的最优解有无数多个,则a的值为 ********* .
12. 给出平面区域(如图),若使目标函数:z=ax+y(a>0)取得最大值的最优解有无数多个,则a的值为 ********* .
13. 不等式![]() 的解集为 ************** 。
的解集为 ************** 。
14. 椭圆![]() 上到点A(1,0)的距离最近的点P的坐标是*************。
上到点A(1,0)的距离最近的点P的坐标是*************。
广东肇庆实验中学2005—2006学年度上学期
月考考试试卷
高二数学答题卡(文科)
一、选择题(每小题5分,共50分)
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 | C | A | D | B | B | C | A | D | B | B |
二、填空题(每小题5分,共20分)
11.x+y-2=0 12. 13. ![]()
14.(![]() )
)
三、解答题(共80分)
 15. (本小题满分14分)如图,在四边形ABCD中,已知AD^CD, AD=10, AB=14, ÐBDA=60°, ÐBCD=135° 求BC的长 .
15. (本小题满分14分)如图,在四边形ABCD中,已知AD^CD, AD=10, AB=14, ÐBDA=60°, ÐBCD=135° 求BC的长 .
解:在△ABD中,
设BD=x,则![]() ………………3分
………………3分
即![]()
整理得:![]() ………………………………8分
………………………………8分
解之:![]()
![]() (舍去) ……………………………… 10分
(舍去) ……………………………… 10分
由正弦定理:
![]() ………………………………12分
………………………………12分
∴![]() ………………………………14分
………………………………14分
 16. (本小题满分14分)在平面直角坐标系xOy中,抛物线y=4x2上异于坐标原点O的两不同动点A、B满足AO⊥BO, 如图所示.求△AOB的重心G(即三角形三条中线的交点)的轨迹方程;
16. (本小题满分14分)在平面直角坐标系xOy中,抛物线y=4x2上异于坐标原点O的两不同动点A、B满足AO⊥BO, 如图所示.求△AOB的重心G(即三角形三条中线的交点)的轨迹方程;
16.(14分)解:(I)设△AOB的重心为G(x,y),A(x1,y1),B(x2,y2),
则 …(1)…… 3分
…(1)…… 3分
∵OA⊥OB ∴![]() ,即
,即![]() ,……(2) …… 6分
,……(2) …… 6分
又点A,B在抛物线上,有![]() ,代入(2)化简得
,代入(2)化简得![]() …… 9分
…… 9分
∴![]()
所以重心为G的轨迹方程为![]() …… 14分
…… 14分
17.(本小题满分14分) 要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格小钢板的块数如下表所示:
| 类 型 | A规格 | B规格 | C规格 |
| 第一种钢板 | 1 | 2 | 1 |
| 第二种钢板 | 1 | 1 | 3 |
|
17.解:设需截第一种钢板![]() 张,第二种钢板
张,第二种钢板![]() 张,所用钢板面积为
张,所用钢板面积为![]() ,
,
 则有
则有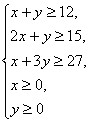 …….5分
…….5分
作出可行域(如图) ………8分
目标函数为![]() …….9分
…….9分
作出一组平行直线![]() (t为参数).由
(t为参数).由![]() 得
得![]() 由于点
由于点![]() 不是可行域内的整数点,而在可行域内的整数点中,点(4,8)和点(6,7)使
不是可行域内的整数点,而在可行域内的整数点中,点(4,8)和点(6,7)使![]() 最小,且
最小,且![]() . …..13分
. …..13分
答:应截第一种钢板4张,第二种钢板8张,或第一种钢板6张,第二种钢板7张,得所需三种规格的钢板,且使所用的钢板的面积最小. ……….14分
18.(本小题满分12分)已知函数![]() 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)求函数![]() 的单调区间.
的单调区间.
18、(Ⅰ)![]() , ………….6分
, ………….6分
(Ⅱ)![]() 在
在![]() 和
和![]() 上是增函数,在
上是增函数,在![]() 上是减函数。
……………12分
上是减函数。
……………12分
 19.(本小题满分14分)
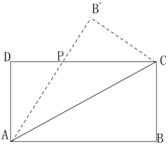
如图,设矩形ABCD(AB>BC)的周长为24,把它沿AC折起来,AB折过去后交DC于点P,设AB=x,求△ADP的面积S的表达式,以及 S的最大值及相应的x的值。
19.(本小题满分14分)
如图,设矩形ABCD(AB>BC)的周长为24,把它沿AC折起来,AB折过去后交DC于点P,设AB=x,求△ADP的面积S的表达式,以及 S的最大值及相应的x的值。
解:由P向AC作垂线交AC于E点(图略),则△PCE与△CAB相似,所以有:
![]() , ………………2分
, ………………2分
又CE=![]() AC,
AC,![]() , ………….4分
, ………….4分
设AB=x,BC=12-x,由AB>BC,可得: 6<x<12, …………….5分
![]() , …………….7分
, …………….7分
从而 PC=![]() ,DP=
,DP=![]() , ………….8分
, ………….8分
△ADP的面积S=![]() ,…………10分
,…………10分
所以S![]() , …………..12分
, …………..12分
当S取最大值时,x满足![]() ,所以x=
,所以x=![]() 。 ………..14分
。 ………..14分
20.(本小题满分12分) 已知椭圆![]() 的离心率是
的离心率是![]() ,F是其左焦点,若直线
,F是其左焦点,若直线![]() 与椭圆交于AB两点,且
与椭圆交于AB两点,且![]() ,求该椭圆的方程。
,求该椭圆的方程。
解:由![]()
![]() …………………….2分
…………………….2分
∴椭圆方程为 ,即
,即![]() …………….4分
…………….4分
将![]() 代入椭圆方程,得:
代入椭圆方程,得:
![]() 整理为
整理为![]() …….7分
…….7分
不妨记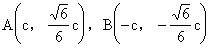 ……………8分
……………8分
又![]()
 …….10分
…….10分
由![]() 得:
得:![]() ………11分
………11分
∴所求的椭圆方程为![]() ………..12分
………..12分
