柳州实验高中2005-2006学年度下学期高二段考数学试卷
（命题人：丁春玲 校对人：向辉）
说明：1.本套试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，共8页，试卷4页，答卷4页.考试时间为120分钟.
2.本卷考试内容：立体几何、排列组合、二项式定理
第Ⅰ卷 选择题（共60分）
一、选择题：（每小题5分，共60分.每小题只有一项正确，请把答案写在答卷上.）
1、一条直线与平面
所成的角为30°，则它和平面内所有直线所成的角中最大的角是（ ）
、30° 
、90°
、150°
、180°
2、已知二面角
为锐角，点
，
到
的距离
，到棱的距离
，则
到的距离是（ ）
、
、 
、
、
3、直线
是异面直线是指⑴ 
且
与
不平行；⑵ 
面，面，且
；⑶ 面，面且 ；⑷ 不存在平面能使面且面成立。上述结论正确的有（ ）
、⑶ ⑷ 、⑴ ⑶ 、 ⑴ ⑷ 、 ⑵ ⑷
4、一个棱锥的侧面积为
，平行于底面的截面分高所成的自上而下的比为1：2，则截面以下部分的侧面积为（ ）
、
、
、
、
5、设地球半径为
，在北纬
圈上有、两地，它们的纬度圈上的弧长等于
，则、两地的球面距离为（ ）
、
、
、
、
6、平行六面体
各棱长都等于4，体积为12，在
上取
，则棱锥
的体积为（ ）
、1 、2 、
、3
7、已知某金属元素的单晶体外形是简单几何体，此晶体有三角形和八边形两种晶面。如果此晶体有24个顶点，以每个顶点为一端都有3条棱，则此晶体的三角形和八边形晶面的数目分别为（ ）
、6和4 、 6和8 、4和6 、8和6
8、正三棱锥
中，
，过作截面与
分别交于
，则截面三角形周长最小值为（ ）
、
、
、
、
9、某电话局的电话号码为
X X X X X，若后面的5位数字是由6或8组成的，则这样的电话号码一共有（ ）个
、
、
、
、
10、某班新年联欢会原定的5个节目已排成节目单，开演前又增加了2个新节目，如果将这2个节目插入原节目单中，那么不同的插入方法有（ ）种
、42 、30
、22
、 12
11、（文科做）下列各组合数中，与
相等的是（
）
、
、
、
、
（理科做）若
，则
的值为（ ）
、
、1
、0
、2
12、椭圆的长轴和短轴把椭圆分成4块，现在用5种不同的颜色给4块涂色，要求共边两块颜色互异，每块只涂一色，共有（ ）种涂色方案
、180
、220
、242
、260
第Ⅱ卷 非选择题（共90分）
二、填空题（每小题4分，共16分，请把答案写在答卷上.）
13、正六边形的1个中心与6个顶点共7个点，以其中3个顶点为顶点的三角形共有 个。
14、在棱长为在正方体中，过
的平面与底面
的交线为
，则直线与
的距离为
。
15、在半径为的一个半球内有一个内接正方体，则这个正方体的棱长为
。
16、已知直线⊥平面，直线
，有下列四个命题：
①∥
⊥,
②⊥∥,
③∥⊥,
④⊥∥,
其中正确命题的序号为________。
三、解答题（共6小题，共74分，请把答案写在答卷上）
17、（12分）证明：若
、
、
、
顺次是
空间四边形各边的中点，且
，
，求证：
是正方形。
18、（12分）从5名男生和3名女生中选出5人担任5门学科的科代表，
（1）求出有女生但人数必须少于男生的选法数；
（2）求出某女生必须担任英语科代表，某男生甲必须担任科代表但不担任语文科代表的选法数。
 |
19、（12分）
是正△
所在平面外一点，
，且
，
，分别是
的中点，求异面直线
所成角的余弦值。
20、（12分）如图，
平面，
，
,求二面角
的大小。
 |
21、（12分）规定
，其中
是正整数，且
，这是组合数
（
是正整数，且
）的一种推广。
（1）求
的值； （2）设
，当
为何值时，
取最小值；
（3）已知组合数是正整数，证明：当
是正整数时，
。
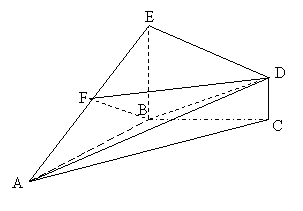
22、（14分）在几何体
中，△是等腰直角三角形，
，
和
都垂直于平面，且
，点是
的中点。
（1）求证：
∥平面； （2）求
与平面
所成角的大小。
 |
柳州实验高中2005-2006学年度下学期高二段考数学试卷答案
(估计平均分93分)
一、选择题（每小题5分，共60分.每小题只有一项正确）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | A | C | B | B | C | D | B | C | A | B | D |
二、填空题（每小题4分，共16分）
13、32
14、
15、
16、①③
三、解答题（共74分）
17、（12分）
证明: ∵、、、顺次是空间四边形各边的中点，
∴
,且
∥
∥
,
∴四边形为平行四边形
又∵
,且，
∴
平行四边形为菱形
又∵
∥
,且，
∴
菱形是正方形
18、（12分）
解：（1）
（2）
19、（12分）
证明： 连结
，取的中点
，连结
，
，
∵为
的中点 ∴∥
∴
为与
所成角
∵
∴
在
△中，
又∵
∴
∴由余弦定理：
20、（12分）
证明： 平面
平面
又∵ ∴
为所求二面角的平面角
在△中, 
在△
中, 
在△
中, 
21、（12分）
解：（1）
（2）
∵
，当且仅当
时，等号成立
∴当时，取最小值。
（3）当
时，组合数
当
时，
当
时，∵
∴
22、（14分）
证明：（1）取
的中点，连结、
∵点是的中点 ∴∥且
又∵∥且
∴∥且
∴四边形
为平行四边形，从而
∥
又∵
平面，
平面
∴∥平面
（2）∵点是的中点
∴点到平面的距离
等于点到平面的距离
∴
在△
中, 
∴
△
为△
过作
于,则
∥
∵
面 ∴
面
∵
∴
∴
设与平面所成角为,则