2004-2005学年度下学期
高中学生学科素质训练
高二数学测试题(7)——空间角和距离
YCY本试卷分第Ⅰ卷和第Ⅱ卷两部分,共150分.
第Ⅰ卷(选择题,共50分)
一、选择题(本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.直线m与平面![]() 间距离为d,那么到m与
间距离为d,那么到m与![]() 距离都等于2d的点的集合是 ( )
距离都等于2d的点的集合是 ( )
A.一个平面 B.一条直线 C.两条直线 D.空集
2.异面直线a、b所成的角为q,a、b与平面a都平行,b^平面b,则直线a与平面b所成的角 ( )
A.与q相等 B.与q互余 C.与q互补 D.与q不能相等.
3.在正方体ABCD—A¢B¢C¢D¢中,BC¢与截面BB¢D¢D所成的角为 ( )
A.![]() B.
B.![]() C.
C.![]() D.arctan2
D.arctan2
4.在正方形SG1G2G3中,E,F分别是G1G2及G2G3的中点,D是EF的中点,现在沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,那么,在四面体S-EFG中必有 ( )
A.SG⊥△EFG所在平面 B.SD⊥△EFG所在平面
C.GF⊥△SEF所在平面 D.GD⊥△SEF所在平面
5.有一山坡,它的倾斜角为30°,山坡上有一条小路与斜坡底线成45°角,某人沿这条小路向上走了200米,则他升高了 ( )
A.100![]() 米 B.50
米 B.50![]() 米 C.25
米 C.25![]() 米 D.50
米 D.50![]() 米
米
6.已知三棱锥D-ABC的三个侧面与底面全等,且AB=AC=![]() ,BC=2,则以BC为棱,以面BCD与面BCA为面的二面角的大小为
( )
,BC=2,则以BC为棱,以面BCD与面BCA为面的二面角的大小为
( )
A.arccos![]() B.arccos
B.arccos![]() C.
C.![]() D.
D.![]()
7.正四面体A—BCD中E、F分别是棱BC和AD之中点,则EF和AB所成的角 ( )
A.45° B.60° C.90° D.30°
8.把∠A=60°,边长为a的菱形ABCD沿对角线BD折成60°的二面角,则AC与BD的距离为 ( )
A.![]() a B.
a B.![]() a C.
a C.![]() a D.
a D.![]() a
a
9.若正三棱锥的侧面均为直角三角形,侧面与底面所成的角为α,则下列各等式中成立的是 ( )
A.0<α<![]() B.
B.![]() <α<
<α<![]() C.
C.![]() <α<
<α<![]() D.
D.![]() <α<
<α<![]()
10.已知A(1,1,1),B(-1,0 ,4),C(2 ,-2,3),则〈![]() ,
,![]() 〉的大小为( )
〉的大小为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题,共100分)
二、填空题(本大题共4小题,每小题6分,共24分)
11.从平面a外一点P引斜线段PA和PB,它们与a分别成45°和30°角,则ÐAPB的最大值是______最小值是_______
12.DABC中ÐACB=90°,PA^平面ABC,PA=2,AC=2,则平面PBC与平面PAC,平面ABC所成的二角的大小分别是______、_________.
13.在三棱锥P-ABC中,![]() ,
,![]() ,BC=5,又PA=PB=PC=AC,则点P到平面ABC的距离是 .
,BC=5,又PA=PB=PC=AC,则点P到平面ABC的距离是 .
14.球的半径为8,经过球面上一点作一个平面,使它与经过这点的半径成45°角,则这个平面截球的截面面积为 .
三、解答题(共计76分)
15.(本小题满分12分)已知SA⊥平面ABC,SA=AB,AB⊥BC,SB=BC,E是SC的中点,
|
(1) 求证:SC⊥面BDE;
(2)求二面角E—BD—C的大小.
16.(本小题满分12分)如图,点![]() 为斜三棱柱
为斜三棱柱![]() 的侧棱
的侧棱![]() 上一点,
上一点,![]() 交
交![]() 于点
于点![]() ,
, ![]() 交
交![]() 于点
于点![]() .
.
(1) 求证:![]() ; (2) 在任意
; (2) 在任意![]() 中有余弦定理:
中有余弦定理:
![]() .拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
.拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
|
17.(本小题满分12分)如图,四棱锥S—ABCD的底面是边长为1的正方形,
SD垂直于底面ABCD,SB=![]() .
.
(1)求证BC![]() SC;
SC;
(2)求面ASD与面BSC所成二面角的大小;
|
大小.
18.(本小题满分12分)在直角梯形ABCD中,ÐD=ÐBAD=90°,AD=DC=![]() AB=a,(如图一)将△ADC 沿AC折起,使D到
AB=a,(如图一)将△ADC 沿AC折起,使D到![]() .记面AC
.记面AC![]() 为a,面ABC为b.面BC
为a,面ABC为b.面BC![]() 为g.
为g.
(1)若二面角a-AC-b为直二面角(如图二),求二面角b-BC-g的大小;
(2)若二面角a-AC-b为60°(如图三),求三棱锥![]() -ABC的体积.
-ABC的体积.
|
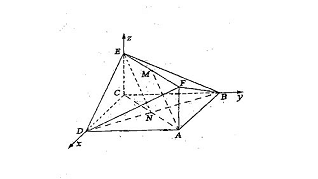
19.(本小题满分14分)如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=![]() ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
(1)求证AM//平面BDE;
(2)求二面角A-DF-B的大小;
(3)试在线段AC上确定一点P,使得PF与BC所成的角是60°.
|
20.(本题满分14分)如图,正方形![]() 、
、![]() 的边长都是1,而且平面
的边长都是1,而且平面![]() 、
、![]() 互相垂直.点
互相垂直.点![]() 在
在![]() 上移动,点
上移动,点![]() 在
在![]() 上移动,若
上移动,若![]()
![]() .
.
(1)求![]() 的长;
的长;
(2)当![]() 为何值时,
为何值时,![]() 的长最小;
的长最小;
(3)当![]() 长最小时,求面
长最小时,求面![]() 与面
与面![]() 所成的二面角
所成的二面角![]() 的大小.
的大小.
|
参考答案(七)
一.选择题(本大题共10小题,每小题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | B | C | A | B | C | A | A | D | D |
二.填空题(本大题共4小题,每小题6分,共24分)
11.750
,150 12.900 ,300 13.![]() 14.
14. ![]()
三、解答题(本大题共6题,共76分)
15.(12分) (1)证明:(1)∵SB=BC E是SC的中点 ∴BE⊥SC ∵DE⊥SC∴SC⊥面BDE
(2)解:由(1)SC⊥BD∵SA⊥面ABC∴SA⊥BD∴BD⊥面SAC∴∠EDC为二面角E-BD-C的平面角
设SA=AB=a,则SB=BC=![]() .
.![]()
![]()
![]() .
.
16.(12分) (1)
证:![]() ;
;
(2) 解:在斜三棱柱![]() 中,有
中,有![]() ,
,
其中![]() 为 平面
为 平面![]() 与平面
与平面![]() 所组成的二面角.
所组成的二面角.

![]() 上述的二面角为
上述的二面角为![]() ,在
,在![]() 中,
中,![]()
![]() ,
,
由于![]() ,
,
![]() 有
有![]() .
.
17.(12分) (1)证法一:如,∵底面ABCD是正方形, ∴BC⊥DC.
∵SD⊥底面ABCD,∴DC是SC在平面ABCD上的射影,

![]() 由三垂线定理得BC⊥SC.
由三垂线定理得BC⊥SC.
证法二:如图1,∵底面ABCD是正方形, ∴BC⊥DC.∵SD⊥底面ABCD,
∴SD⊥BC,又DC∩SD=D,∴BC⊥平面SDC,∴BC⊥SC.
(2)解:如图2,过点S作直线![]()
![]() 在面ASD上,
在面ASD上,
∵底面ABCD为正方形,![]() 在面BSC上,
在面BSC上,
![]() 为面ASD与面BSC的交线.
为面ASD与面BSC的交线.
![]()
![]()
∴∠CSD为面ASD与面BSC所成二面角的平面角.(以下同解法一)
![]() (3)解1:如图2,∵SD=AD=1,∠SDA=90°,
(3)解1:如图2,∵SD=AD=1,∠SDA=90°,
 ∴△SDA是等腰直角三角形.又M是斜边SA的中点,
∴△SDA是等腰直角三角形.又M是斜边SA的中点,
∴DM⊥SA.∵BA⊥AD,BA⊥SD,AD∩SD=D,∴BA⊥面ASD,SA是SB在面ASD上的射影.由三垂线定理得DM⊥SB.
∴异面直线DM与SB所成的角为90°.
![]() 解2:如图3,取AB中点P,连结MP,DP.在△ABS中,由中位线定理得
MP//SB,
解2:如图3,取AB中点P,连结MP,DP.在△ABS中,由中位线定理得
MP//SB,![]() 是异面直线DM与SB所成的角.
是异面直线DM与SB所成的角.![]() ,又
,又![]()
∴在△DMP中,有DP2=MP2+DM2,![]()
∴异面直线DM与SB所成的角为90°.
18.(12分) 解:(1)在直角梯形ABCD中,
由已知![]() DAC为等腰直角三角形,
DAC为等腰直角三角形,
∴ ![]() , 过C作CH⊥AB,由AB=2
, 过C作CH⊥AB,由AB=2![]() ,
,
可推得 AC=BC=![]() ∴ AC⊥BC .取 AC的中点E,连结
∴ AC⊥BC .取 AC的中点E,连结![]() ,
,
则 ![]() ⊥AC 又 ∵ 二面角
⊥AC 又 ∵ 二面角![]() 为直二面角,
为直二面角,
∴ ![]() ⊥
⊥![]() 又 ∵
又 ∵ ![]() 平面
平面![]() ∴ BC⊥
∴ BC⊥![]() ∴ BC⊥
∴ BC⊥![]() ,而
,而![]() ,
,
∴ BC⊥![]() ∴
∴ ![]() 为二面角
为二面角![]() 的平面角.
的平面角.
由于![]() , ∴二面角
, ∴二面角![]() 为
为![]() .
.
(2)取AC的中点E,连结![]() ,再过
,再过![]() 作
作![]() ,垂足为O,连结OE.
,垂足为O,连结OE.
∵ AC⊥![]() , ∴ AC⊥
, ∴ AC⊥![]() ∴
∴
![]() 为二面角
为二面角![]() 的平面角,
的平面角,
∴ ![]()
![]() . 在
. 在![]() 中,
中,![]() ,
,
∴![]()
![]()
![]()
![]()
 19.(14分)解法一: (1)记AC与BD的交点为O,连接OE, ∵O、M分别是AC、EF的中点,ACEF是矩形,∴四边形AOEM是平行四边形,
19.(14分)解法一: (1)记AC与BD的交点为O,连接OE, ∵O、M分别是AC、EF的中点,ACEF是矩形,∴四边形AOEM是平行四边形,
∴AM∥OE.∵![]() 平面BDE,
平面BDE, ![]() 平面BDE,∴AM∥平面BDE.
平面BDE,∴AM∥平面BDE.
(2)在平面AFD中过A作AS⊥DF于S,连结BS,∵AB⊥AF, AB⊥AD, ![]() ∴AB⊥平面ADF,∴AS是BS在平面ADF上的射影,
∴AB⊥平面ADF,∴AS是BS在平面ADF上的射影,
由三垂线定理得BS⊥DF.∴∠BSA是二面角A—DF—B的平面角.
在RtΔASB中,![]()
∴![]() ∴二面角A—DF—B的大小为60º.
∴二面角A—DF—B的大小为60º.
(3)设CP=t(0≤t≤2),作PQ⊥AB于Q,则PQ∥AD,
∵PQ⊥AB,PQ⊥AF,![]() ,∴PQ⊥平面ABF,
,∴PQ⊥平面ABF,![]() 平面ABF,∴PQ⊥QF.在RtΔPQF中,∠FPQ=60º,PF=2PQ.
平面ABF,∴PQ⊥QF.在RtΔPQF中,∠FPQ=60º,PF=2PQ.
∵ΔPAQ为等腰直角三角形,∴![]() 又∵ΔPAF为直角三
又∵ΔPAF为直角三
角形,∴![]() ,∴
,∴![]() 所以t=1或t=3(舍去),即点P是AC的中点.
所以t=1或t=3(舍去),即点P是AC的中点.
解法二: (1)建立如图所示的空间直角坐标系.
设![]() ,连接NE, 则点N、E的坐标分别是(
,连接NE, 则点N、E的坐标分别是(![]() 、(0,0,1),
、(0,0,1),
 ∴
∴![]() , 又点A、M的坐标分别是
, 又点A、M的坐标分别是![]() ,(
,(![]()
∴![]() =(
=(![]() ∴
∴![]() 且NE与AM不共线,∴NE∥AM.又∵
且NE与AM不共线,∴NE∥AM.又∵![]() 平面BDE,
平面BDE, ![]() 平面BDE,∴AM∥平面BDF.
平面BDE,∴AM∥平面BDF.
(2)∵AF⊥AB,AB⊥AD,AF![]() ∴AB⊥平面ADF.
∴AB⊥平面ADF.
∴![]()
![]() 为平面DAF的法向量.
为平面DAF的法向量.
 ∵
∵![]() =(
=(![]() ·
·![]() =0,
=0,
∴![]() =(
=(![]() ·
·![]() =0得
=0得
![]() ,
,![]() ,∴NE为平面BDF的法向量.
,∴NE为平面BDF的法向量.
∴cos<![]() =
=![]() ∴AB与NE的夹角是60º.即所求二面角A—DF—B的大小是60º.
∴AB与NE的夹角是60º.即所求二面角A—DF—B的大小是60º.
(3)设P(t,t,0)(0≤t≤![]() )得
)得![]()
![]() ∴
∴![]() =(
=(![]() ,0,0)
,0,0)
又∵PF和BC所成的角是60º.∴
 解得
解得![]() 或
或![]() (舍去),即点P是AC的中点.
(舍去),即点P是AC的中点.
20.(14分) 解:(1)作![]() ∥
∥![]() 交
交![]() 于点
于点![]() ,
,![]() ∥
∥![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,依题意可得
,依题意可得![]() ∥
∥![]() ,且
,且![]()
![]()
![]() ,即
,即![]() 是平行四边形∴
是平行四边形∴![]()
![]()
![]()
由已知![]() ,
,![]()
∴![]() 又
又![]() ,
,![]() ,
,
即![]()
∴![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(2)由(Ⅰ),![]()
![]()
![]() ,所以,当
,所以,当![]() 时,
时,![]()
![]()
![]()
即![]() 、
、![]() 分别移动到
分别移动到![]() 、
、![]() 的中点时,
的中点时,![]() 的长最小,最小值为
的长最小,最小值为![]() .
.
(3)取![]() 的中点
的中点![]() ,连结
,连结![]() 、
、![]() ,∵
,∵![]() ,
,![]() ,
,![]() 为
为![]() 的中点
的中点
∴![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,∠
,∠![]() 即为二面角
即为二面角![]() 的平面角,又
的平面角,又![]()
![]()
![]()
![]() ,所以,由余弦定理有
,所以,由余弦定理有 , 故所求二面角
, 故所求二面角![]()





