高二数学期中专训(1)

高二期中专训(1)

一、选择题（共10小题，每小题4分，共40分）

1. 已知a、b、cR，下列命题中正确的是（　　 ）

　  （A）. a＞bac²＞bc²　　　　 （B）. ac²＞bc²a＞b　　 

（C）. a³＞b³　　　　 （D）a²＞b²a＞│b│

2. 直线L的方向向量为（-1，2），则该直线的倾斜角为（　　 ）

（A）arctan2　　　(B)arctan（-2）　　　 （C）π+arctan2　　　（D）π-arctan2　

3. 不等式│x²-2│＜1的解集为（　　　 ）

（A）{x│-1＜x＜　　　　　  (B){x│-1＜x＜1或x＞

（C）{x│-＜x＜-1或1＜x＜}　（D）{x│x＜1或1＜x＜

4. 下列命题：①│x+│的最小值是2　 ②的最小值是2　③log₂x+log_x2的最小值是2　④0＜x＜，tanx+cotx的最小值是2　⑤3^x+3^-x的最小值是2，则正确的命题个数：（　 ）

（A）1　　（B）2　　 （C）3　　　 （D）4

5. 直线L经过A（2，1）、B（1，m²）两点（mR），那么直线L的倾斜角的取值范围是（　　　）

（A）[0，π]　　　　  （B）[0，]∪（，π）　

（C）[0，]　　　　  （D）[0，]∪[，π]

6. 若已知直线L₁∶x-2y+4=0，L₂过点P（-2，1），若直线L₁到L₂的角为45°，则直线L₂的方程为（　　　）

（A）x-y-1=0　　　　　 （B）x-3y+5=0　　　(C)3x+y-7=0　　(D)3x-y+7=0

7. 是│a+1│＜1的（　　　）

（A）充分不必要条件　　（B）必要不充分条件　

（C）充要条件　　 　　　（D）既不充分也不必要条件

8. 已知f (x)=，a、b为两个不相等的正实数，则下列不等式正确的是（　　 ）

　　（A）f（　　　　  （B）

（C）　　　　　 (D)

9. 过点(2，3)且在两坐标轴上截距的绝对值相等的直线的条数是(　　)

　　(A)1　　　　(B)3　 　　(C)4　　　　(D)2

　　(重点中学做)过点P(1，2)且和坐标轴围成的三角形面积为4的直线条数是(　　)

　　(A)4　　　　  (B)3　　　　　　(C)2　　　　　　 (D)1

10. (普通中学做)将进货单价为80元的商品按90元一个出售能卖出400个，已知这种

　　 商品每个涨价1元，其销售量就减少20个，为了赚取最大利润，售价应定为每个(　　)

　　(A)95元　 　　　　　　　 (B)100元

　　(C)105元　　　　　　　　 (D)110元

　  (重点中学做)要挖一个半圆柱形的鱼池，其池面为圆柱的轴截面，若池面周长为定值2a，则此鱼池的最大容积为(　　)　

　　(A)　　　　　　　　  (B)

　　(C)　　　　　　　　  (D)

二、填空题：(共4小题，每小题4分，共16分)　

　　11. 点(3，1)和(-4，6)在直线3x-2y+a=0的两侧，则a的取值范围是______________.

　　12. 光线从点M(-2，3)射到x轴上一点P(1，0)后被x轴反射，则反射光线所在的直线方程_________.

　　13. 已知A(2，-1)，B(5，3)，直线l：2x-y+1=0与AB所在直线相交于点P，则点P分有向线段AB所成的比λ的值为_________.

　　14. (普通中学做)若a>0，b>0且满足ab≥1+a+b，则a+b最小值是_________.

　　14. (重点中学做)已知x，y∈R⁺，且x²+=1，则x的最大值是___________.

三、简答题：(15、16题各6分，17题12分，18、19题各6分，20题8分，共44分)

　　15. 解不等式：<

　　16. 证明不等式：设a、b都是正数，x、y∈R，且a+b=1，求证：(ax+by)²≤ax²+by²

　　17. 当m为何值时，直线l₁：x+my+6=0，l₂：(m-2)x+3y+m=0

　　①l₁⊥l₂ ③l₁//l₂③l₁、l₂重合

　　18. 两平行直线l₁、l₂分别过点P(0，1)Q(，0)　　

　　(1)求l₁、l₂之间的距离d的范围

　　(2)当l₁与l₂距离最远时，过A(1，1)的一条直线l被它们截得的线段长为4，求直线l的方程.

　　19. 药片A每片中含成分α为5g，成分β为2g；药片B每片中含成分α为3g，成分β为3g；A每片2角，B每片1角5分，若应至少服用20g的α和10g的β时，应服用A、B各几片既符合要求又省钱. (g：克)

　　20. (普通中学做)设函数f(x)是定义在[-1，1)上的奇函数，且对任意点a、b∈[-1，1]

　　当a+b≠0时都有>0

　　(1)证明：函数f(x)是在[-1，1]上的增函数.

　　(2)解不等式f(x-)<f(x-)

　　(重点中学做)已知f(x)的定义域为(0，+∞)且在其上为增，满足f(xy)=f(x)+f(y)，f(2)=1

　　①求f(8)②解不等式f(x)+f(x-2)<3

高二期中专训(1)

数学参考答案及评分标准

一、选择题：（4’×10=40’）

题号	1	2	3	4	5	6	7	8	9	10
答案	B	D	C	D	B	D	D	A	B	A

二、填空题（每小题4分，共16分）

11. {a│-7＜a＜24}　　  12. x-y-1=0 　　　　13. λ= -

14. 2+2（普）　 （重）

二、简答题（15、16题各6分，17题12分，18、19题各6分，20题8分，共44分）

15. P30　13（2）（略）（6分）　　16. P17，7（略）（6分）

17. 解：（1）（4分）l₁⊥l₂ （m-2）+3m=0　 m=

　　　　　　　　　　　　　 3-m（m-2）=0

（2）（4分）l₁⊥l₂ 　　　　　　　 m= -1或m=3

　　　　　　　　　  m²-18≠0

　　　　　　　　　  3-m（m-2）=0

（3）l₁与l₂重合　　　　　　　　 无解，不可能重合　　　 （4分）

　　　　  　　　　　m²-18=0

18. 解：（1）0＜d≤2　　　　　　　　　　　　　　　　　　　　　　  （2分）

（2）当l₁、l₂距离最远时，则l₁、l₂应都与直线PQ垂直，此时l被截得的线段的长为4，则直线l与l₁所成的角为arcsin

∵k_l1=

由tan

∴所求直线l的方程为y-1=（x-1）即x-y+-1=0

经检验，当直线l与x轴垂直时，也符合题意，

此时l的方程为x=1

综上所述，求直线l的方程为x=1和x-y+-1=0 （4分）

19. 解：设应服A片，B片y片，根据题意，得到约束条件为

5x+3y≥20

2x+3y≥10

x≥0

y≥0　　x、yN

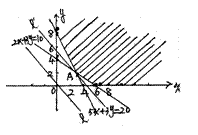
目标函数为z=20x+15y作出可行区域作直线l∶20x+15y=0，

如图把直线l向右上方平行移动

至l＇，则l＇过可行区域上点A，解方程组

5x+3y=20

　　　　  得A()

2x+3y=10

因不是整数，因此点A不是最优解。

考虑最接近A的整数点（4，1）、（3，2）并进行比较，过（4、1）时，z=95

过（3，2）时，z=90，因此（3，2）点为最优解，即服用A3片，B2片既合乎要求又省钱。

20. （普）

证明：（1）任取x₁、x₂[-1,1]且x₁＜x₂，则-x²[-1,1]

又∵f（x）是奇函数

∴f (x₁)-f(x₂)=f (x₁)+f (-x₂)=

∵＞0　x₁-x₂＜0

∴f (x₁)-f(x₂)＜0即f (x₁)＜f (x₂)

∴f (x)在[-1,1]上是增函数（4分）

（2）∵f (x)是[-1,1]上的增函数

　　　　　　　　　　　  -1≤x-≤1

∴f (x-)＜f (x-)　　-1≤x-≤1

　　　　　　　　　　　  -1≤x-≤x-

解得{x│-≤x≤}　　　　　　　　　 （4分）

（重）解：（1）由题意得f (4)=f (2)+f (2)=2　

3=2+1=f (4)+f (2)=f (4×2)=f (8)　　　　　　 （4分）

（2）∵f (x)+f(x-2)=f (x²-2x)＜f (8)

∴原不等式可化为f (x²-2x)＜f (8)

x²-2x＜8

得　 x -2＞0　　　　2＜x＜4 解集为{x│2＜x＜4}　　 （4分）

x＞0