高二数学期末复习(一)
一.选择题
1.如果ac<0,且bc>0,那么直线ax+by+c=0不通过 ( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
2.直线mx+ny+3=0在y轴上的截距为–3,而且它的倾斜角是直线![]() x–y=3
x–y=3![]() 倾斜角的2倍,则
( )
倾斜角的2倍,则
( )
(A)m=–![]() ,
n=1 (B)m=–
,
n=1 (B)m=–![]() ,
n=–3 (C)m=
,
n=–3 (C)m=![]() ,n=–3 (D)m=
,n=–3 (D)m=![]() ,n=1
,n=1
3.直线l过点P(–1, 2),且与以A(–2, –3), B(4, 0)为端点的线段相交,则l的斜率的取值范围是 ( )
(A)[–![]() ,
5]
(B)[–
,
5]
(B)[–![]() ,
0)∪(0, 5]
,
0)∪(0, 5]
(C)(–∞, –![]() ]∪[5,
+∞) (D)[–
]∪[5,
+∞) (D)[–![]() ,
,![]() )∪(
)∪(![]() ,
5]
,
5]
4.“m=–2”是“直线(2–m)x+my+3=0与直线x–my–3=0垂直”的 ( )
(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)不充分不必要条件
5.如果命题“坐标满足方程f(x, y)=0的点都在曲线C上”是假命题,那么下列命题中为真命题的是 ( )
(A)坐标满足方程f(x, y)=0的点都不在曲线C上
(B)坐标满足方程f(x, y)=0的点有些在曲线C上,有些不在曲线C上
(C)一定有不在曲线C上的点,其坐标满足方程f(x, y)=0
(D)不在曲线C上的点,其坐标一定不满足方程f(x, y)=0
6.若圆(x–3)2+(y+5)2=r2上有且只有两个点到直线4x–3y=2的距离等于1,则半径r的取值范围是 ( )
(A)(4, 6) (B)[4, 6) (C)(4, 6] (D)[4, 6]
7.直线3x–4y–5=0和圆![]() (θ为参数)的位置关系是
( )
(θ为参数)的位置关系是
( )
(A)相交但不过圆心 (B)相交且过圆心 (C)相切 (D)相离
8完成一项装修工程,请木工需付工资每人50元,请瓦工需付工资每人40元,现有工人工资预算2000元,设木工x人,瓦工y人,请工人的约束条件是 ( )
(A)50x+40y=2000 (B)50x+40y≤2000 (C)50x+40y≥2000 (D)40x+50y≤2000
9.直线Ax+By+C=0右下方有一点(m, n),则Am+Bn+C的值 ( )
(A)与A同号,与B同号 (B)与A同号,与B异号
(C)与A异号,与B同号 (D)与A异号,与B异号
10.设实数x, y满足(x–2)2+y2=3,那么![]() 的最大值是 (
)
的最大值是 (
)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
11.如果直线l将圆x2+y2–2x–4y=0平分,且不通过第四象限,则l的斜率的取值范围是( )
(A)[0, 2] (B)[0, 1] (C)[0, ![]() ] (D)[–
] (D)[–![]() ,
0]
,
0]
12.若y=1+![]() (–2≤x≤2)与y=k(x–2)+4有两个不同的交点,则k的取值范围是 (
)
(–2≤x≤2)与y=k(x–2)+4有两个不同的交点,则k的取值范围是 (
)
(A)(![]() ,
, ![]() ] (B)[
] (B)[![]() ,
, ![]() ) (C)(
) (C)(![]() ,
, ![]() ) (D)[
) (D)[![]() ,
, ![]() ]
]
二.填空题:
13.已知圆的方程是x2+y2+4x–4y+4=0,则该圆上距离原点最近的点是 ;最远的点是 .
14.平面上有两点P(m+2, n+2), Q(n–4, m–6),且这两点关于4x+3y–11=0对称,则m= ;n= .
15.已知直线l1: y=![]() x+2,直线l2过点P(–2, 1),且l1到l2的角为45°,则l2的方程是
.
x+2,直线l2过点P(–2, 1),且l1到l2的角为45°,则l2的方程是
.
16.设R为平面上以A(4, 1), B(–1, –6), C(–3, 2)三点为顶点的三角形区域(包括边界及内部),则点P(x, y)在R上运动时,函数u=4x–3y的最大值和最小值分别为 .
三.解答题:
17.一直线过点P(–5, –4)且与两坐标轴围成的三角形的面积是5,求此直线的方程.
18.已知直线l: x+y–2=0,一束光线从点P(0, 1+![]() )以120°的倾角投射到直线l上,经l反射,求反射光线所在直线的方程.
)以120°的倾角投射到直线l上,经l反射,求反射光线所在直线的方程.
19.一个圆经过点P(2, –1),和直线x–y=1相切,并且圆心在直线y=–2x上,求它的方程.
20. 求经过直线2x+y+4=0和圆x2+y2+2x–4y+1=0的交点,且面积最小的圆的方程.
高二数学期末复习(二)
一.选择题
1.点P在直线2x+y+10=0上,PA, PB与圆x2+y2=4分别相切于A, B两点,则四边形PAOB面积的最小值为 ( )
(A)24 (B)16 (C)8 (D)4
2.若圆x2+y2=r2(r>0)上恰有相异的两点到直线4x-3y+25=0的距离等于1,则r的取值范围是 ( )
(A)[4, 6] (B)[4, 6) (C)(4, 6] (D)(4, 6)
3.已知P为椭圆![]() 上第三象限内一点,且它与两焦点的连线互相垂直,若点P到直线4x-3y-
上第三象限内一点,且它与两焦点的连线互相垂直,若点P到直线4x-3y-
(A)[-7, 8] (B)[-![]() ,
, ![]() ] (C)[-2, 2] (D)(-∞,-7]∪[8, +∞)
] (C)[-2, 2] (D)(-∞,-7]∪[8, +∞)
4.设椭圆![]() ,双曲线
,双曲线![]() ,抛物线y2=2(m+n)x(m>n>0)的离心率分别为e1, e2, e3,则
( )
,抛物线y2=2(m+n)x(m>n>0)的离心率分别为e1, e2, e3,则
( )
(A)e1e2>e3 (B)e1e2<e3 (C)e1e2=e3 (D)e1e2与e3大小不定
5.过椭圆![]() (a>0)的焦点F作一直线交椭圆于P, Q两点,若线段PF与QF的长分别为p, q,则
(a>0)的焦点F作一直线交椭圆于P, Q两点,若线段PF与QF的长分别为p, q,则![]() 等于
( )
等于
( )
(A)![]() (B)
(B)![]() (C)
(C)
6.已知对称轴为坐标轴的双曲线的渐近线方程为y=±![]() (a>0, b>0),若双曲线上有一点M(x0, y0)使ay0>bx0,那么双曲线的焦点
( )
(a>0, b>0),若双曲线上有一点M(x0, y0)使ay0>bx0,那么双曲线的焦点
( )
(A)在x轴上 (B)在y轴上 (C)当a>b时在x轴上 (D)当a<b时在y轴上
7.双曲线C的一个顶点到相应准线的距离与这个点到另一焦点的距离的比为λ,则λ的取值范围是 ( )
(A)(0, 1) (B)(0, ![]() ) (C)(0, 3-2
) (C)(0, 3-2![]() ) (D)(
) (D)(![]() ,
3-2
,
3-2![]() )
)
8.过双曲线x2-![]() =1的右焦点F作直线l交双曲线于A, B两点,若AB=4,则这样的直线l有
( )
=1的右焦点F作直线l交双曲线于A, B两点,若AB=4,则这样的直线l有
( )
(A)1条 (B)2条 (C)3条 (D)4条
9.直线l过双曲线![]() 的右焦点,斜率k=2,若l与双曲线的两个交点分别在左、右两支上,则此双曲线的离心率e的取值范围是
( )
的右焦点,斜率k=2,若l与双曲线的两个交点分别在左、右两支上,则此双曲线的离心率e的取值范围是
( )
(A)e>![]() (B)1<e<
(B)1<e<![]() (C)1<e<
(C)1<e<![]() (D)e>
(D)e>![]()
10.曲线2px-y2=0(p>0)与直线2kx-2y-k=0(k≠0)的交点为P1(x1, y1), P2(x2, y2),那么y1y2的值是 ( )
(A)与k无关的负数 (B)与k无关的正数
(C)与k有关的负数 (D)与k有关的正数
二.填空题
11.在椭圆![]() (a>b>0)中,左焦点为F,右顶点为A,短轴上方端点为B,若离心率e=
(a>b>0)中,左焦点为F,右顶点为A,短轴上方端点为B,若离心率e=![]() ,则∠ABF=
.
,则∠ABF=
.
12.设点P是双曲线x2-![]() =1上一点,焦点F(2,0),点A(3,2),使PA+
=1上一点,焦点F(2,0),点A(3,2),使PA+![]() PF有最小值时,则点P的坐标是
.
PF有最小值时,则点P的坐标是
.
13.已知P为y2=4x上一点,记P到此抛物线的准线的距离为d1,P到直线x+2y-12=0的距离为d2,则d1+d2的最小值为 .
14.AB是抛物线y=x2的一条弦,若AB的中点到x轴的距离为1,则弦AB的长度的最大值为 .
三.解答题
15.设F1, F2分别为椭圆C: ![]() (a>b>0)的左、右两个焦点,
(a>b>0)的左、右两个焦点,
(1)若椭圆C上的点A(1, ![]() )到F1, F2两点的距离之和等于4,写出椭圆C的方程;
)到F1, F2两点的距离之和等于4,写出椭圆C的方程;
(2)设K是(1)中所得椭圆上的动点,求线段F1K的中点的轨迹方程;
16.已知抛物线y2=2px (p>0),在x轴上是否存在一点M,使过M的任意直线l(x轴除外),与抛物线交于A(x1,
y1), B(x2, y2)两点,且总有∠AOB=![]() (O为坐标原点),试证明你的结论。
(O为坐标原点),试证明你的结论。
17.已知曲线C是与两个定点M1(-4![]() ,
0), M2(-2
,
0), M2(-2![]() ,
0)的距离的比为
,
0)的距离的比为![]() 的点的轨迹,直线l过点(-2
的点的轨迹,直线l过点(-2![]() ,
5)且被曲线C截得的线段的长等于4,求曲线C和直线l的方程.
,
5)且被曲线C截得的线段的长等于4,求曲线C和直线l的方程.
18.设椭圆![]() ,过点P(0, 3)的直线l与椭圆交于不同的A, B两点,且A位于P, B之间,令λ=
,过点P(0, 3)的直线l与椭圆交于不同的A, B两点,且A位于P, B之间,令λ=![]() ,求λ的取值范围.
,求λ的取值范围.
19.已知椭圆C的中心在原点,焦点在x轴上,一条准线的方程是x=1,倾斜角为![]() 的直线l交椭圆C于A, B两点,且AB的中点坐标为(-
的直线l交椭圆C于A, B两点,且AB的中点坐标为(-![]() ,
,![]() ),求椭圆C的方程.
),求椭圆C的方程.
20.已知圆C过定点A(0, a) (a>0),且在x轴上截得的弦MN的长为
(1)求圆C的圆心的轨迹方程;
(2)设AM=m, AN=n,求![]() 的最大值及此时圆C的方程.
的最大值及此时圆C的方程.
 21.如图所示,过圆O: x2+y2=4与y轴正半轴的交点A作圆的切线l,M为l上任意一点,再过M作圆的另一切线,切点为Q,当M点在直线l上移动时,求△MAQ的垂心的轨迹方程.
21.如图所示,过圆O: x2+y2=4与y轴正半轴的交点A作圆的切线l,M为l上任意一点,再过M作圆的另一切线,切点为Q,当M点在直线l上移动时,求△MAQ的垂心的轨迹方程.
22.已知⊙C: (x–3)2+(y–4)2=1,点A(–1, 0), B(1, 0),点P是圆上的动点,求d=PA2+PB2的最值及对应的点P的坐标.
高二数学期末复习(三)
一.选择题
1.方程x2+y2+2ax-2ay=0表示的圆 ( )
(A)关于直线y=x对称 (B)关于直线x+y=0对称
(C)过原点且圆心在x轴上 (D)过原点且圆心在y轴上
2.椭圆![]() (a>b>0)的左焦点到左准线的距离是
( )
(a>b>0)的左焦点到左准线的距离是
( )
(A)a-c (B)a-b (C)![]() (D)
(D)![]()
3.双曲线![]() 的离心率e∈(1, 2),则k的取值范围是
( )
的离心率e∈(1, 2),则k的取值范围是
( )
(A)(0, 6) (B)(3, 12) (C)(1, 3) (D)(0, 12)
4.抛物线y=x2上的点到直线2x-y=4的最短距离是 ( )
(A)![]() (B)
(B)![]()
![]() (C)
(C)![]()
![]() (D)
(D)![]()
![]()
5.双曲线![]() 上的点P到点(5, 0)的距离是15,则点P到点(-5, 0)的距离是( )
上的点P到点(5, 0)的距离是15,则点P到点(-5, 0)的距离是( )
(A)7 (B)23 (C)5或25 (D)7或23
6.椭圆![]() 上的点M到焦点F1的距离是2,N是MF1的中点,则ON为 ( )
上的点M到焦点F1的距离是2,N是MF1的中点,则ON为 ( )
(A)4 (B)2 (C)8 (D)![]()
7.已知0<r<![]() +1,则两圆x2+y2=r2与(x-1)2+(y+1)2=2的位置关系是
( )
+1,则两圆x2+y2=r2与(x-1)2+(y+1)2=2的位置关系是
( )
(A)相切 (B)相交 (C)外离 (D)内含
8.若AB是抛物线y2=18x的一条过焦点F的弦,AB=20, AD、BC垂直于y轴,D、C分别为垂足,则梯形ABCD的中位线的长是 ( )
(A)5 (B)10 (C)![]() (D)
(D)![]()
9.从动点P(a, 2)向圆(x+3)2+(y+3)2=1作切线,则切线长的最小值为 ( )
(A)4 (B)2![]() (C)5 (D)
(C)5 (D)![]()
10.双曲线kx2+4y2=4k的离心率小于2,则k的取值范围是 ( )
(A)(-12, 0) (B)(-3, 0) (C)(-∞, 0) (D)(-60, -12)
11.已知曲线y=![]() 与直线x+y-m=0有两个不同的交点,则m的取值范围是(
)
与直线x+y-m=0有两个不同的交点,则m的取值范围是(
)
(A)(0,![]() -1)(B)[0,
-1)(B)[0,![]() -1)(C)(-2,
-1)(C)(-2,![]() -1)(D)(-
-1)(D)(-![]() -1,
-1,![]() -1)
-1)
12.设P为抛物线y=x2上的一个动点,则定点A(a, 0)关于P点的对称点Q的轨迹方程是( )
(A)y=![]() (x-a)2
(B)y=
(x-a)2
(B)y=![]() (x+a)2 (C)y=
(x+a)2 (C)y=![]() (x+
(x+
二.填空题
13.
以椭圆![]() +y2=1的右焦点F为焦点,以原点为顶点做抛物线,抛物线与椭圆准线的一个交点为A,则AF=
.
+y2=1的右焦点F为焦点,以原点为顶点做抛物线,抛物线与椭圆准线的一个交点为A,则AF=
.
14.双曲线![]() 与椭圆
与椭圆![]() 有共同的焦点,则m=
.
有共同的焦点,则m=
.
15.已知定点A(3, 2)在抛物线y2=2px (p>0)的内部,F为抛物线的焦点,点Q在抛物线上,当AQ+QF取最小值4时,p= .
16.已知直线y=kx+1与曲线x2-y-8=0的两个交点关于y轴对称,则这两个交点的坐标是 .
三.解答题
17.已知抛物线的顶点在原点,焦点在y轴上,抛物线上一点(a, -3)到焦点的距离等于5,求a的值,并写出抛物线的方程,准线方程,焦点坐标.
18.半径为5的圆过点A(-2, 4),并且以M(-1, 3)为中点的弦长为4![]() ,求此圆的方程.
,求此圆的方程.
19.椭圆ax2+by2=1与直线x+y=1相交于A、B两点,若AB=2![]() ,且AB的中点C与椭圆中心连线的斜率为
,且AB的中点C与椭圆中心连线的斜率为![]() ,求a, b的值.
,求a, b的值.
20.若抛物线y=ax2-1上存在A, B两点关于直线l: x+y=0对称,求实数a的取值范围.
21.已知圆C: x2+y2+6x-91=0及圆内一点P(3, 0),求过点且与已知圆相内切的圆的圆心M的轨迹方程.
22.已知直线l的方程为y=mx+m2(m∈R),抛物线C1的顶点和双曲线C2的中心都在坐标原点,且它们的焦点都在y轴上,
(1)当m=1时,直线l与抛物线C1有且只有一个公共点,求抛物线C1的方程;
(2)若双曲线C2的两个焦点和虚轴的一个端点组成的三角形的面积为8,且当m≠0时,直线l过C2的一个焦点和虚轴的一个端点,求双曲线C2的方程.高二数学期末复习(四)
一.选择题
1.圆x2+y2+2x+6y+9=0与圆x2+y2-6x+2y+1=0的位置关系是 ( )
(A)相离 (B)相外切 (C)相交 (D)相内切
2.椭圆(1-m)x2-my2=1的长轴长是 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.椭圆的两个焦点和中心把两准线间的距离四等分,则一焦点与短轴两端点连线的夹角是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]() ( )
( )
4.“ab<
(A)必要不充分条件 (B)充分不必要条件
(C)充要条件 (D)非充分非必要条件
5.设F1, F2是椭圆![]() 的两个焦点,P在椭圆上,已知P, F1,
F2是一个Rt△的三个顶点,且P F1>P F2,则P F1 : P F2的值是
( )
的两个焦点,P在椭圆上,已知P, F1,
F2是一个Rt△的三个顶点,且P F1>P F2,则P F1 : P F2的值是
( )
(A)![]() 或2
(B)
或2
(B)![]() 或
或![]() (C)
(C)![]() 或
或![]() (D)
(D)![]() 或2
或2
6.已知点F(![]() ,
0),直线l: x=-
,
0),直线l: x=-![]() ,点B是l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线相交于点M,则点M的轨迹是
(
)
,点B是l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线相交于点M,则点M的轨迹是
(
)
(A)双曲线 (B)椭圆 (C)圆 (D)抛物线
7.直线x-2y-3=0与圆x2+y2-4x+6y+4=0交于A, B两点,C为圆心,则△ABC的面积是
(A)2![]() (B)4
(B)4![]() (C)
(C)![]() (D)2
(D)2![]() (
)
(
)
8.以双曲线![]() 的右焦点为圆心,且与两条渐近线相切的圆的方程是 (
)
的右焦点为圆心,且与两条渐近线相切的圆的方程是 (
)
(A)(x+5)2+y2=9 (B)(x+5)2+y2=16
(C)(x-5)2+y2=9 (D)(x-5)2+y2=16
9.若椭圆![]() (m>n>0)与双曲线
(m>n>0)与双曲线![]() (s>0, t>0)有相同的焦点F1和F2(m≠s),P是两曲线的一个公共点,则PF1·PF2的值是
( )
(s>0, t>0)有相同的焦点F1和F2(m≠s),P是两曲线的一个公共点,则PF1·PF2的值是
( )
(A)![]() (B)m-s (C)
(B)m-s (C)![]() (D)
(D)![]()
10.过P(1, 0)的直线l与抛物线y2=2x交于两点M, N,O为原点,若kOM+kON=1,则直线l的方程是 ( )
(A)2x-y-1=0 (B)2x+y+1=0 (C)2x-y-2=0 (D)2x+y-2=0
二.填空题:
11.若实数x, y满足(x-2)2+y2=1,则![]() 的取值范围是
.
的取值范围是
.
12.圆心在x轴上,经过原点,并且与直线y=4相切的圆的一般方程是
.
13.椭圆x2+4y2=16被直线y=x+1截得的弦长为 .
14.以抛物线y2=4x的焦点为圆心,且被抛物线的准线截得的弦长为2的圆的方程是 .
三.解答题:
15.已知圆的方程x2+y2=25,点A为该圆上的动点,AB与x轴垂直,B为垂足,点P分有向线段BA的比λ=![]() .
.
(1) 求点P的轨迹方程并化为标准方程形式;
(2) 写出轨迹的焦点坐标和准线方程.
16.已知椭圆的中心在原点,焦点在x轴上,连接它的四个顶点得到的四边形的面积是4![]() ,分别连接椭圆上一点(顶点除外)和椭圆的四个顶点,连得线段所在四条直线的斜率的乘积为
,分别连接椭圆上一点(顶点除外)和椭圆的四个顶点,连得线段所在四条直线的斜率的乘积为![]() ,求这个椭圆的标准方程.
,求这个椭圆的标准方程.
17.设抛物线y2=2px (p>0)上各点到直线3x+4y+12=0的距离的最小值为1,求p的值.
18.直线y=x+b与双曲线2x2-y2=2相交于A, B两点,若以AB为直径的圆过原点,求b的值.
19.已知椭圆的中心在原点,准线为x=±4![]() ,若过直线x-
,若过直线x-![]() y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点,
y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点,
(1)求椭圆的方程;
(2)求过左焦点F1且与直线x-![]() y=0平行的弦的长.
y=0平行的弦的长.
 20.如图,已知F(0, 1),直线l: y=-2,圆C: x2+(y-3)2=1,
20.如图,已知F(0, 1),直线l: y=-2,圆C: x2+(y-3)2=1,
(1)若动点M到点F的距离比它到直线l的距离小1,求动点M的轨迹E的方程;
(2)过轨迹E上一点P作圆C的切线,当四边形PACB的面积S最小时,求点P的坐标及S的最小值。
参考答案
一.选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | B | C | A | D | D | A | D | B | D |
二.解答题:
11.[-![]() ,
, ![]() ]
12.x2+y2±8x=0
]
12.x2+y2±8x=0
13.![]() 14.(x-1)2+y2=5
14.(x-1)2+y2=5
三.解答题
15.设点P(x, y)是轨迹上任意一点,点A的坐标是(x1, y1), 点B的坐标是(x1, 0),
∵点P分有向线段BA的比λ=![]() ,
,
∴ 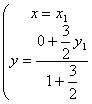 , ∴
, ∴  , 又点A在圆x2+y2=25上,
, 又点A在圆x2+y2=25上,
∴ x2+![]() y2=25, 即
y2=25, 即![]() (y≠0),
(y≠0),
椭圆![]() 的焦点坐标是(-4, 0), (4,
0), 准线方程是x=±
的焦点坐标是(-4, 0), (4,
0), 准线方程是x=±![]() .
.
16.设所求的方程为![]() (a>b>0), 椭圆上一点为P(x0,
y0),
(a>b>0), 椭圆上一点为P(x0,
y0),
则椭圆的四个顶点分别为(a, 0), (-a, 0), (0, b), (0, -b),
由已知四直线的斜率乘积为![]() ,得
,得![]() =
=![]() ,
,
∵ b2x02+a2y02=a2b2, ∴ y02=![]() , x02=
, x02=![]() ,
,
代入得![]() =
=![]() , 又由已知2ab=4
, 又由已知2ab=4![]() , 及a>0, b>0,
得a=2, b=
, 及a>0, b>0,
得a=2, b=![]() ,
,
∴ 椭圆
方程是![]() =1.
=1.
17.设P(x0, y0)为抛物线y2=2px上任意一点,则P到直线3x+4y+12=0的距离
S=![]() , 将x0=
, 将x0=![]() 代入得S=
代入得S= ,
,
∵ S的最小值是1, ∴ 8p-![]() >0(否则若8p-
>0(否则若8p-![]() ≤0,得S的最小值为0) 且当y0=-
≤0,得S的最小值为0) 且当y0=-![]() 时,
时, ![]() =1, 解得p=
=1, 解得p=![]() .
.

高二数学期末复习(五)
一、选择题
1、F是定直线l外的定点,以F为焦点,l为相应准线的椭圆有 ( )
(A)1个 (B)2个 (C)3个 (D)无数个
2、直线ax+3y-9=0与直线x-3y+b=0关于原点对称,则a、b的值是 ( )
(A)a=1,b=9 (B)a=-1,b=9 (C)a=1,b= -9 (D)a= -1,b= -9
3、已知两点M(0,1),N(10,1),给出下列直线方程: ①5x-3y-22=0; ②5x-3y-52=0
③x-y-4=0;④4x-y-14=0。在直线上存在P满足MP=NP+6的所有直线方程是 ( )
(A)①②③ (B)②④ (C)①③ (D)②③
4、若直线![]() 与圆
与圆![]() 有两个公共点,那么点
有两个公共点,那么点![]() 与圆
与圆![]() 的
的
位置关系是(A)点在圆上(B)点在圆内 (C)点在圆外(D)不能确定
5、已知抛物线![]() 的过焦点的弦AB被焦点分成长为
的过焦点的弦AB被焦点分成长为![]() 、
、![]() 的两段,那么 ( )
的两段,那么 ( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
6、当0 < a < 1时,方程ax2+y2=1表示的曲线是 ( )
(A)圆 (B)焦点在x轴上的椭圆 (C) 焦点在y轴上的椭圆 (D)双曲线
7、下列命题中一定正确的是 ( )
(A)到两定点距离之和为常数的点的轨迹是椭圆 (B)到定直线![]() 和定点F(-c,0)的距离之比为
和定点F(-c,0)的距离之比为![]() )的点的轨迹是椭圆 (C)到定点F(-c,0)和定直线
)的点的轨迹是椭圆 (C)到定点F(-c,0)和定直线![]() 的距离之比为
的距离之比为![]() (a>c>0)的点的轨迹是左半个椭圆 (D) 到定直线
(a>c>0)的点的轨迹是左半个椭圆 (D) 到定直线![]() 和定点F(c,0)的距离之比为
和定点F(c,0)的距离之比为![]() (a>c>0)点的轨迹是椭圆
(a>c>0)点的轨迹是椭圆
8、过抛物线焦点F的直线与抛物线相交与A、B两点,若A、B在抛物线的准线上的射影分别是A![]() 、B
、B![]() ,则∠A
,则∠A![]() FB
FB![]() 为
( )
为
( )
(A)45° (B) 60° (C)90° (D)120°
9、点P![]() (x
(x![]() ,y
,y![]() )是直线
)是直线![]() : f(x,y)=0上的一点,直线
: f(x,y)=0上的一点,直线![]() 外一点P
外一点P![]() (
(![]() ),则
),则
方程f(x,y)-f(x![]() ,y
,y![]() )-f(x
)-f(x![]() ,y
,y![]() )=0表示的直线
( )
)=0表示的直线
( )
(A)与![]() 重合 (B)过P
重合 (B)过P![]() 与
与![]() 垂直 (C) 过P
垂直 (C) 过P![]() 与
与![]() 平行 (D)过 P
平行 (D)过 P![]() 与
与![]() 相交
相交
10、点(![]() )在圆x
)在圆x![]() +y
+y![]() -2y-4=0的内部,则
-2y-4=0的内部,则![]() 的取值范围是
( )
的取值范围是
( )
(A)-1<![]() <1 (B)
0<
<1 (B)
0<![]() <1 (C) –1<
<1 (C) –1<![]() <
<![]() (D) -
(D) -![]() <
<![]() <1
<1
11、方程![]() 表示的曲线为
( )
表示的曲线为
( )
(A)直线 (B)椭圆 (C)双曲线 (D)抛物线
12、以椭圆两焦点为直径端点的圆交椭圆于不同的四点,顺次连接四个交点和两个焦点恰好围成一个正六边形,则这个椭圆的离心率为 ( )
(A)![]() -
-![]() (B)
(B)![]() -1 (C)
-1 (C)![]() (D)
(D)![]()
二、填空题
13、与直线3x-4y+1=0平行且距离为2的直线方程为___________________.
14、从椭圆的焦点A(-1,0)发出的光线经反射后到达点B(5,0),最短路程为10,则这椭圆的方程是___________________ .
15、菱形的一个内角为![]() ,边长为4,一椭圆经过它的两个顶点,并以它的另外两个顶点为焦点,则椭圆的标准方程是___________________.
,边长为4,一椭圆经过它的两个顶点,并以它的另外两个顶点为焦点,则椭圆的标准方程是___________________.
16、已知直线y=-![]() x + 4与抛物线y2=2px (p>0) 交于两点A、B,若OA⊥OB,则p的值为 ___________________.
x + 4与抛物线y2=2px (p>0) 交于两点A、B,若OA⊥OB,则p的值为 ___________________.
三、解答题
17、求与双曲线![]() 有公共焦点,且经过点A(
有公共焦点,且经过点A(![]() )的椭圆方程.
)的椭圆方程.
18、设椭圆中心为O,过椭圆的一个焦点引直线l与椭圆交于A、B两点,如果能使
∠AOB=90°,试求椭圆离心率的最小值,并求出此时直线l与椭圆长轴的夹角.翰林汇
19、试根据![]() 的不同取值,讨论圆
的不同取值,讨论圆![]() 与抛物线
与抛物线![]() 的公共点的情况.
的公共点的情况.
20、一船在水面上的高度为![]() ,测得河面宽
,测得河面宽![]() .
.![]() 米).
米).
21、已知椭圆具有性质:若A是椭圆C的一条与x轴不垂直的弦的中点,那么该弦的斜率等于点A的横、纵坐标的比值与某一常数的积.试对双曲线![]() 写出具有类似特性的性质,并加以证明.
写出具有类似特性的性质,并加以证明.