高二上期末练习

高二上期末练习题（三）

　　　　　　　　　　　　　　　　　　　　　  姓名--------------------

1．x＞4是＜的　　　　　　　　　　　　　　　　　　　　　　　 　　　 （　　）

A．必要不充分条件　　　　　　　　　　　 B．充要条件

C．充分不必要条件　　　　　　  　　　　 D．既不充分又非必要条件

2．过点（2，1）的直线中被圆x²+y²-2x+4y=0截得的弦长最大的直线方程是　　　（　　）

A．3x-y-5=0　　　　 B．3x+y-7=0　　　 C．x+3y-5=0　 　　　　D．x-3y+5=0

3．直线l：ax+4my+3a=0(m≠0)，过点（1，－1），那么l的倾斜角为　　　　　　（　　）

A．arctan　　　　 B．arctan(－)　　C．π－arctan　　D．π－arctan4

4．曲线2px－y²=0(p>0)与直线2kx－2y－k=0(k≠0)的交点为P₁(x₁, y₁), P₂(x₂, y₂)，那么y₁y₂的值是　　　　　  　　　　　　　　　　　　　　　　　　　　　　　　　（ 　 ）

A．与k无关的负数　　　　　 　　　　　　　B．与k无关的正数

C．与k有关的负数　　　　　 　　　　　　　D．与k有关的正数

5．在下列函数中，当x取正数时，最小值为2的是　　　　　　　　　　　　　　（　　）

A．y=x+　　　　　　　　　　  　　 　 B．

C．　　　　　　　 D．y=x²－2x+3

6．若0＜a＜1，0＜b＜1，则a+b，2，a²+b²，2ab中最大一个是　　　　　　（　  ）

A．a+b　　　 B．2　　　　　 C．a²+b²　　　　　D．2ab

7．如果直线l将圆：x²+y²－2x－4y=0平分，且不过第四象限，那么l的斜率取值范围是（　　）

A．[0，2]　　　　　　　　　　　　 B．（0，2）

C．（－∞，0）∪（2，+∞）　　　　 D．（－∞，0∪[2，+∞

8．过双曲线的右焦点F₂作垂直于实轴的弦PQ, F₁是左焦点,

若∠PF₁Q=90⁰, 则双曲线的离心率为　　　　　　　　　　 　　　　　　　　　　(　　)

A. 　 　　　　B. 1+　　　　C. 2+　　　　　　　　D. 3-

9．设x、y满足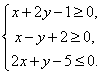则的最大值是　　　　　　　　　　  （　 　）

A. 4　　　　　　  B. 3　　　　　　　  C. 2　　　　　　　　  D. 1

10．使x－4+x－5＜a有实数解的a为　　　　　　　　　　　　　　　　　　 （　 　）

A．a＜1　　　 　 B．1＜a＜9　　　　 C．a＞1　　　　　　　D．a≥1

11. 已知两点A( –2, 0 ) , B( 0 , 2 ), 点P是椭圆=1上任意一点，则点P到直线AB距离的最大值是　　　　　　　　　　　　　　　　　　　　　　　　　　　   （　　）

A． .　　 　　B．3.　　　　  C．.　　 　　　 D．0.

12、双曲线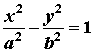 (0<a<b)的半焦距为c，直线L过两点(a , 0),(0 , b)，且双曲线的中心到直线L的距离为，则双曲线的离心率为　　（　　）

A． 2 　　　 　B． 　　　　　C． 　　 　　 D．

13．函数(x＞－1)的最小值是　　　　　　　  .

14．过点P（3，0）作直线l，使它被两相交直线2x－y－2=0和x+y+3=0所截得的线段中点恰好被P点平分，则直线l的方程是　　　　　　　  .

15．已知圆的方程为x²+y²+ax+2y+a²=0，一定点A（1，2），要使过定点A（1，2）作圆的切线有两条，则a的范围是　　　　　　　  .

16．将a千克的白糖加水配制成b千克糖水（b＞a＞0），则其浓度为　　　　；若再加入m千克白糖（m＞0），糖水更甜了，根据这一生活常识提炼出一个常见不等式　　  .

17．已知抛物线 y ² = – x与直线 y = k ( x + 1 )相交于A、B两点, 点O是坐标原点.

(1) 求证: OA^OB;

(2) 当△OAB的面积等于时, 求k的值.

高二上期末练习题（三）答案

1.C　2.A 　 3.C 　 4.Ａ  　5.D

6.A　7.A 　 8.Ｂ 　9.Ａ 　 10.Ｃ　　 11.Ａ 　12.A

13．9

14．8x－y－24=0　

15．α∈()　

16．＜

17．解：

（１）　将y = k ( x + 1 )代入 y ² = – x消去y得：

　　　　

　　　　

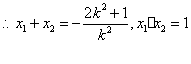
　　　同理可得：

　即：OA^OB;

（２）设原点到直线y = k ( x + 1 )的距离为d,则

　　　

　　　

　　　

　　　由（１）知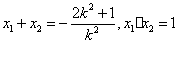：代入上式解得：

　　　　　　　，经检验都满足，所以．