高二数学期中复习试题（一）
第Ⅰ卷（选择题 共50分）
一、选择题：本大题共10小题，每小题5分，共50分．
1.若直线
与
互相平行,则
值为（ ）
A.
B.
C.或
D.
或
2.已知三条直线
，设
与
的夹角为
，到
的角为
，则
＝（ ）
A.45
B.75
C. 105
D.135
3．下列命题中： ⑴ 若两条直线平行，则其斜率必相等；
⑵ 若两条直线的斜率乘积为－1, 则其必互相垂直；
⑶ 过点（－1，1），且斜率为2的直线方程是
；
⑷ 若直线的倾斜角为
，则
。
其中为真命题的有（ ）.
A. 1个 B. 2个 C. 3个 D. 4个
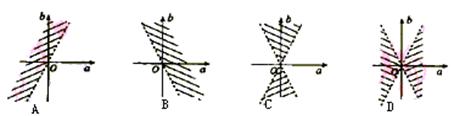
4．如果函数
的图象与x轴无交点，则点（a，b）在aOb平面上的区域（不包含边界）为
（ ）
|
5.曲线y=2x2上的点到直线x+y+1=0的距离最小值为（ ）
A.
B.
C.
D.
6.若直线ax+y+2=0和线段PQ相交，其中P(－2，1)，Q（3，2），则a的取值范围是（ ）
A. 
B. 
C. 
D. 
7.点M（x，y）在直线x+2y+1=0上移动，函数f(x，y)＝
的最小值是（ ）
A. 
B. C. 
D. 
8.直线
左移3个单位，再上移1个单位时，恰回到原来的位置，则直线的斜率是（ ）
A.
B.－3
C.
D. 3
9.点P（2，4）在直线ax+y+b=0上的射影是点Q（4，3），则a与b的值依次是（ ）
A.－2，5 B. 2，－11 C. 
，－5
D. 
，－1
10.设A、B是x轴上的两点，点P的横坐标为2且PA=PB，若直线PA的方程为x-y+1=0，则直线PB的方程是（ ）
A. x+y-5=0 B.2x-y-1=0 C.2x-y-4=0 D.2x+y-7=0
第Ⅱ卷（非选择题 共100分）
二、填空题：本大题共6小题，每小题4分，共24分．
11.若不等式
的解集是[－1，2]，
的解集为
，且f(x)与g(x)的定义域都是R，那么不等式
的解集是_____________________；
12.设全集
则
=__________________；
13.在下面等号右侧两个分数的分母括号处，各填上一个自然数，并且使得这两个自然数的和最小：
。
14.设a、b、c是正数，则
的最小值是__________________；
15.某厂建造一个长方体无盖水池，其容积为
，深为
，若池低造价
，池壁造价
，
则怎样设计水池总造价最低，最低总造价是____________________.
16.若直线
与直线
关于直线
对称，则
，b= 。
三．解答题：7题，共36分，解答应写出文字过程，证明过程或演算步骤
17. 本小题满分10分
解关于x的不等式(1)
(2)
18.本小题满分12分
已知向量
＝（3，－4），
＝（6，－3），
＝（5－m，－(3＋m)）。
①若点A、B、C能构成三角形，求实数m应满足的条件；
②若△ABC为直角三角形，且
为直角，求实数m的值。
19.本小题满分12分
将一张画了直角坐标系且两轴的长度单位相同的纸折叠一次，使点P(2，0)与点Q(－2，4)重合，若点（5，8）与点（m，n）重合，求m+n的值。
20.本小题满分12分
求分别满足下列条件的直线方程：
（1）
求经过点
且在坐标轴上的截距相等的直线方程
（2） 倾斜角是直线3x+4y+5=0的倾斜角的2倍，且过点（2，-1）的直线方程
21.本小题满分12分
某工厂库存A, B, C三种原料，可以用来生产甲、乙两种产品，市场调查显示可获利润等各数据如下表，
| A | B | C | 每件产品利润(元) | ||
| 库存量(件) | 100 | 125 | 156 | （1） | （2） |
| 甲(每件用料) | 1 | 2 | 3 | 2000 | 1000 |
| 乙(每件用料) | 4 | 3 | 1 | 1000 | 3000 |
问：若市场调查如（1），怎样安排生产能获得最大利润；若市场调查如（2），怎样安排生产能获得最大利润。
22. 本小题满分8分
光线从点A（-3，4）出发射到x轴上，被x轴反射到y轴上，又被y轴反射后到点B(-1,6),则光线所经过的路程为多少？
23.本小题满分10分
已知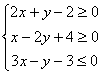
，
在x，y取何值时取得最大值与最小值？最大值和最小值各是多少？