第七章 直线与圆的方程
第1课时 直线的方程
1、下面命题中正确的是( )
(A)经过定点P0(x0,y0)的直线都可以用方程y-y0=k(x-x0)表示.
(B)经过任意两个不同的点P1(x1,y1),P2(x2,y2)的直线都可以用方程(y-y1)(x2-x1)=(x-x1)(y2-y1)表示
(C)不经过原点的直线都可以用方程![]() 表示
表示
(D)经过点A(0,b)的直线都可以用方程y=kx+b表示
2、如果AC〈0且BC〈0,那么直线Ax+By+C=0不通过( )
(A)、第一象限 (B)、第二象限 (C)、第三象限 (D)、第四象限
3、过点P(1,1)作直线L与两坐标轴相交所得三角形面积为10,直线L有( )
(A)、一条 (B)、两条 (C)、三条 (D)、四条
4、直线2x-y-4=0绕它与x轴的交点逆时针旋转450,所得的直线方程是_______
5、直线L过点A(0,-1),且点B(-2,1)到L的距离是点![]() 到L的距离的两倍,则直线L的方程是_______
到L的距离的两倍,则直线L的方程是_______
6、已知![]() 是直线L的倾斜角,且sin
是直线L的倾斜角,且sin![]() +cos
+cos![]() =
=![]() ,则直线L的斜率为__________.
,则直线L的斜率为__________.
7、直线L在两坐标轴上的截距之和为12,又直线L经过点(-3,4),则直线L的方程为_________
8、当a+b+c=0时,直线ax+by+c=0必过定点_______
9、过点P(1,4),作直线与两坐标轴的正半轴相交,当直线在两坐标轴上的截距之和最小时,求此直线方程.
10、已知两点A(-1,-5),B(3,-2),直线L的倾斜角是直线AB的倾斜角的一半,求直线L的斜率.
11、已知圆C:(x-2)2+(y-1)2=1,求过A(3,4)的圆C的切线方程.
12、求函数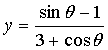 的值域.
的值域.
答案: 1:B; 2:B ; 3:D; 4:y=-3x+6;
5x-y-1=0; 6:-![]() ;
;
7:3x+9y-27=0或16x-4y+64=0 ;8: (1,1)
9:解:![]() 设所求直线L的方程为:
设所求直线L的方程为:![]()
∵直线L经过点P(1,4)
∴![]()
![]()
∴![]()
![]()
当 且仅当![]()
![]() 即a=3,b=6时a+b有最小値为9,此时所求直线方程为2x+y-6=0。
即a=3,b=6时a+b有最小値为9,此时所求直线方程为2x+y-6=0。
10.解:设直线L的倾斜角为![]() ,则直线AB的倾斜角为2
,则直线AB的倾斜角为2![]() 。
。
∴kAB=tan2![]() =
=![]()
又tan2![]()
![]() 或
或![]()
![]()
![]() 00≤2
00≤2![]() <1800,∴00≤
<1800,∴00≤![]() <900
<900
![]() ∴
∴![]()
![]() ∴
∴![]()
![]()
![]()
![]() ∴直线的斜率为
∴直线的斜率为![]()
![]() 11.解:设过A(3,4)的直线y-4=k(x-3),即kx-y+4-3k=0
11.解:设过A(3,4)的直线y-4=k(x-3),即kx-y+4-3k=0
![]() 由
由![]() 得k=
得k=![]()
∴切线方程为![]() ,即4x-3y=0
,即4x-3y=0
 但过A(3,4)向圆可作两条切线,一条从斜率不存在的直线中去找,一条切线为x=3
但过A(3,4)向圆可作两条切线,一条从斜率不存在的直线中去找,一条切线为x=3
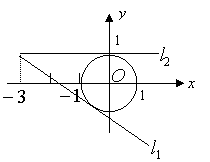
12.解:![]() 可以看成两点A(
可以看成两点A(![]() ,B(-3,1)
,B(-3,1)
连线的斜率,B为定点,A为动点,动点A的轨为单位圆)
如图,只需求直出直线l1的斜率k1即可
不难求出k1=-![]() ,又k2=o
,又k2=o
∴由图可知,定点B与动点A连
线的斜率K的范围为,![]() ,
,
故原函数的值域为![]() 。
。
第2课时 直线与直线的位置关系
1、已知集合M={(x,y)∣x+y=2},N={(x,y)∣x-y=4},那么集合M∩N为( )
A. {3,-1} BCD{(3,-1)}
2、已知点M(a,b),若点N与M关于x轴对称,点P与N关于y轴对称,点P与点Q关于直线x+y=0对称,则点Q的坐标为( )
A. (a,b) B. (b,a) C. (-a,-b) D.(-b,-a)
3、已知直线2x+2y-2=0和mx-y+1=0的夹角为![]() ,那么m的值为( )
,那么m的值为( )
A. -![]() 或-3 B.
或-3 B.![]() 或
或![]() 或3 D.
或3 D.![]() 或-3
或-3
4、已知两直线l1:y=x,l2:ax-y=0,其中a为实数,当这两条直线的夹角在(0,![]() )内变动时,a的取值为( )
)内变动时,a的取值为( )
A. (0,1) B. (![]() ,
,![]() ) C.(
) C.( ![]() ,1)
,1)![]() (1,
(1,![]() ) D.(1,
) D.(1,![]() )
)
5、已知直线ax+3y+1=0与直线x+(a-2)y+a=0,当a= 时,两直线平行,
当a= 时,两直线重合;当a![]() 时,两直线相交.
时,两直线相交.
6、已知曲线C:y=x2,则它关于x-y-2=0对称的曲线方程是
7、直线ax+4y-2=0与2x-5y+c=0垂直于点(1,m),则a= c= m=
8、已知P是直线l上的一点,将直线l绕点P逆时针方向旋转角![]() ),所得的直线方程为l1:3x-y-4=0,若继续绕P点逆时针方向转
),所得的直线方程为l1:3x-y-4=0,若继续绕P点逆时针方向转![]() ,则得直线l2的方程为x+2y+1=0,求直线l的方程.
,则得直线l2的方程为x+2y+1=0,求直线l的方程.
9、已知正方形ABCD的相对顶点A(0,-1)和C(2,5),求顶点B和D的坐标。
10、已知椭圆C的直角坐标方程为![]() ,试确定m的取值范围,使得对于直线y=4x+m,椭圆C上有不同的两点关于该直线对称。
,试确定m的取值范围,使得对于直线y=4x+m,椭圆C上有不同的两点关于该直线对称。
1、D 2、B 3、C.4、C 5. 3,-1,{a![]() 且
且![]() }
}
6.x=y2+4y+6 7、10,-12,-2
8、解:P点的坐标为直线3x-y-4=0与 x+2y+1=0的交点,即(1,-1)所求的直线与l2垂直,故斜率k=2,所以l的方程为y+1=2(x-1),即:2x-y-3=0
9、解:AC中点P(1,2),因为kAC=3,所以KBD=-![]() ,直线BD的方程y-2=-
,直线BD的方程y-2=-![]() (x-1),即x+3y-7=0,直线AC的方程为3x-y-1=0,又
(x-1),即x+3y-7=0,直线AC的方程为3x-y-1=0,又![]() B和D的坐标满足方程组
B和D的坐标满足方程组
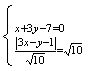 ,解之得
,解之得![]() 或
或![]() 即B、D的坐标分别为(4,1)及(-2,3)。
即B、D的坐标分别为(4,1)及(-2,3)。
10、解:椭圆C有不同的两点关于直线l:y=4x+m对称,其充要条件是直线l1:y=![]() x+n与椭圆C有两个不同的交点P,Q,且P.Q的中点在l上。由
x+n与椭圆C有两个不同的交点P,Q,且P.Q的中点在l上。由
![]() 13x2-8nx+16n2-48=0
13x2-8nx+16n2-48=0
![]() x1
x1![]() x2
x2
所以![]() =64n2-52(16n2-48)>0, 所以
=64n2-52(16n2-48)>0, 所以 ![]()
又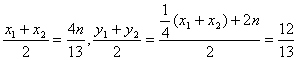 ,PQ中点在l上,
,PQ中点在l上,
所以![]()
第3课时 线性规划
1、已知![]() ,则在不等式
,则在不等式![]() 表示的平面区域内的点是( )
表示的平面区域内的点是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、不等式![]() 表示的平面区域在直线
表示的平面区域在直线![]() 的( )
的( )
A、右上方 B、右下方 C、左上方 D、左下方
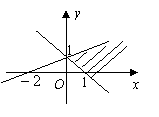 3、如图中阴影部分表示的平面区域可用二元一次不等式组表示成( )
3、如图中阴影部分表示的平面区域可用二元一次不等式组表示成( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
4、已知x, y满足
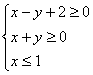
则![]() 的最值为( )
的最值为( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
5、下列说法正确的是( )
A、线性规划问题中的最优解是指目标函数的最大值或最小值;
B、线性规划问题中的可行解是使目标函数取得最大值或最小值的变量x、y的值;
C、如果线性规划问题中的可行域的边界是一条折线,那么最优解必是某一顶点的坐标;
D、线性规划问题中的最优解是指使目标函数取得最大值或最小值的变量x、y的实际可能的值.
6、△ABC的三顶点为![]() ,则△ABC的内部可用二元一次不等式组表示为
。
,则△ABC的内部可用二元一次不等式组表示为
。
7、已知集合![]() ,
,![]() ,
,![]() ,则M的面积等于
。
,则M的面积等于
。
8、设x、y满足 ,则
,则![]() 的最小值为 ,最大值为 。
的最小值为 ,最大值为 。
9、某电脑用户计划使用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装磁盘。若软件至少买3片,磁盘至少买2盒,则不同的选购方式有多少种?
10、某厂要生产甲种产品45个,乙种产品55个,所用原料为A、B两种规格的金属板,每张面积分别为
11、A1,A2两煤矿分别有煤8万吨和18万吨,需通过外运能力分别为20万吨和16万吨的B1,B2两车站外运,用汽车将煤运到车站,A1的煤运到B1,B2的运费分别为3元/吨和5元/吨,A2的煤运到B1,B2的运费分别为7元/吨和8元/吨。问如何编制调运方案,可使总运费最少?
1、C 2、B 3、A 4、B 5、D
6、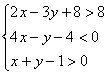 7、1 8、
7、1 8、![]()
9、设软件买x片,磁盘买y盒,则
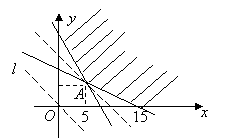
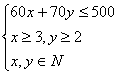 可行解有7个,故不同的选购方式有7种。
可行解有7个,故不同的选购方式有7种。
10、设A种取x块,B种取y块,总用料为z m2,则
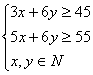
![]()
可行域如图,最优解为A(5,5),x=5,y=5时,![]() ,即A、B两种各取5块时可保证完成任务,且总的用料(面积)最省为
,即A、B两种各取5块时可保证完成任务,且总的用料(面积)最省为
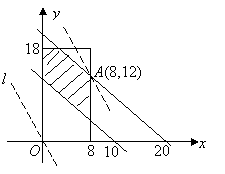 11、设A1运到B1x万吨,A2运到B1y万吨,总运费为z万元,则A1运到B2
11、设A1运到B1x万吨,A2运到B1y万吨,总运费为z万元,则A1运到B2![]() 万吨,A2运到B2
万吨,A2运到B2![]() 万吨,
万吨,![]() 满足
满足
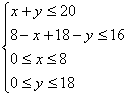
可行域如图,当![]() 时,
时,![]() ,
,
即A1的8万吨煤全运到B1,A2运12万吨运到B1,
剩余6万吨运到B2,这时总运费最少为156万元。
第4课时 圆的方程
1.以两点A(-3,-1)和B(5,5)为直径端点的圆的方程是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
2.![]() 且
且![]() 是方程
是方程![]() 表示圆的( )
表示圆的( )
A.充分非必要条件 B、必要非充分条件
C、充要条件 D、既非充分也非必要条件
3.如果方程![]() 表示一个圆,则k的取值范围是( )
表示一个圆,则k的取值范围是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4.若圆C1的方程是![]() ,
,
圆C2的方程为![]() ,则两圆的公切线有( )
,则两圆的公切线有( )
A、2条 B、3条 C、4条 D、1条
5.圆![]() 关于A(1,2)对称的圆的方程为
关于A(1,2)对称的圆的方程为
6.圆![]() 上的动点Q到直线
上的动点Q到直线![]() 距离的最小值为
距离的最小值为
.
7、已知圆方程是![]() ,分别根据下列条件,写出a、b、r满足的条件:
,分别根据下列条件,写出a、b、r满足的条件:
(1)若圆与y轴相切,则 .
(2)若圆与两坐标轴都相切,则 .
8、求圆心在直线![]() 上,且过点A(1,2),
上,且过点A(1,2),![]() 的圆的方程
的圆的方程
9、已知圆A的圆心在曲线![]() 上,圆A与y轴相切,又与另一圆
上,圆A与y轴相切,又与另一圆![]() 相外切,求圆A的方程.
相外切,求圆A的方程.
10、求一宇宙飞船的轨道,使在轨道上任一点处离地球和月球的视角都相等.
11、已知点A(3,0),P是圆![]() 上任意一点,∠AOP的平分线交PA于M(O为原点),试求点M的轨迹.
上任意一点,∠AOP的平分线交PA于M(O为原点),试求点M的轨迹.
1.C 2. B 3.B 4. D 5. ![]() .
.
6.
![]() , 7.(1)
, 7.(1)![]() .(2)
.(2)![]() .
.
8、![]() .
.
9、解:设圆A圆心坐标为![]() ,半径为r,依题有
,半径为r,依题有
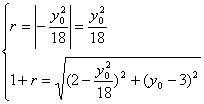
解之得:![]() 或
或![]()
∴ 所求圆A的方程为:![]() 或
或![]()
10、设地球、月球半径分别为R、r,球心距为d,以地球月球球心连线的中心为原点,连线所在直线为x轴建立直角坐标系。(如图)则点![]() ,
,![]() 设轨道上任一点
设轨道上任一点![]() ,从M点向⊙O1、⊙O2分别作切线,切点为P、Q,依题意有:
,从M点向⊙O1、⊙O2分别作切线,切点为P、Q,依题意有:![]() 故
故![]() ∽
∽![]() ,
,
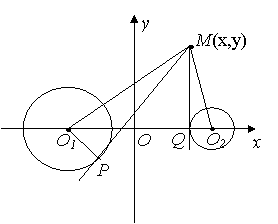 则
则 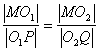 ,故有
,故有
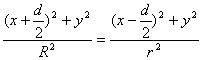
整理得:![]()
其轨迹是圆.
11、设![]() ,则
,则![]()
设![]() ,则
,则
![]()
∵ ![]()
![]()
![]()
∴ ![]()
故点M的轨迹方程是:![]() (点
(点![]() 除外)
除外)
第5课时 直线与圆、圆与圆的位置关系
1、 圆x2+y2-2axcos![]() -2bysin
-2bysin![]() -a2sin2
-a2sin2![]() =0在x轴上截得的弦长为
( )
=0在x轴上截得的弦长为
( )
A. ![]() C.
C.![]() D. 4
D. 4![]()
2、 已知直线ax+by+c=0(abc![]() 0)与圆x2+y2=1相切,则三条边长分别为
0)与圆x2+y2=1相切,则三条边长分别为![]() 的三角形( )
的三角形( )
A. 是锐角三角形 B.是直角三角形 C.是钝角三角形 D.不存在
3、一动圆与圆(x-2)2+y2=1及y轴都相切,则动圆圆心的轨迹是( )
A. 一点 B. 两点 C. 一条抛物线. D. 两条抛物线
4、 直线![]() 截圆x2+y2=4得劣弧所对的圆心角为( )
截圆x2+y2=4得劣弧所对的圆心角为( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
5、 经过点P(6,-4),且被圆x2+y2=20截得的弦长为6![]() 的直线方程为
的直线方程为
6、 自直线y=x上点向圆x2+y2-6x+7=0引切线,则切线长的最小值为
7、 已知一动圆与圆C1: x2+y2+2x-4y+1=0外切,并且和定圆C2: x2+y2-10x-4y-71=0内切,求动圆圆心的的轨迹方程。
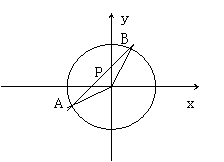 8、由点P(0,1)引圆x2+y2=4的割线l,交圆于A,B两点,使ΔAOB的面积为
8、由点P(0,1)引圆x2+y2=4的割线l,交圆于A,B两点,使ΔAOB的面积为![]() (O为原点),求直线l的方程。
(O为原点),求直线l的方程。
9、点A(0,2)是圆x2+y2=16内的定点,点B,C是这个圆上的两个动点,若BA⊥CA,求BC中点M的轨迹方程,并说明它的轨迹是什么曲线。
10、已知与曲线C: x2+y2-2x-2y+1=0相切的直线l与x轴、y轴的正半轴交于两点A、B,O为原点,OA=a,OB=b(a>2,b>2)
(1)求证:曲线C与直线l相切的条件是(a-2)(b-2)=2 ;
(2)求ΔAOB面积的最小值。
1.B 2.B 3. D.4.C. 5.x+y-2=0或7x+17y+26=0 6.![]() .
.
7.解:圆C1的圆心为O1(-1,2),r1=2,圆C2的圆心为O2(5,2),r2=10
设动圆圆心为G(x,y),则![]()
整理得:![]()
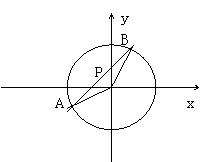 8、解:设直线l的方程为y=kx+1
①
8、解:设直线l的方程为y=kx+1
①
将①代入圆的方程整理得(1+k2)x2+2kx-3=0 ②
设其二实数根为x1,x2,由根与系数的关系得 O
x1+x2=![]() ,x1x2=
,x1x2=![]()
设点A(x1,y1),B(x2,y2)
![]()

即![]()
解得k=![]() ,故直线l的方程为y=
,故直线l的方程为y=![]() x+1
x+1
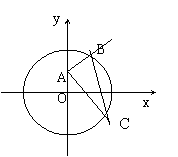 9、解:设点M(x,y),因为M是定弦BC的中点,故OM⊥BC,
9、解:设点M(x,y),因为M是定弦BC的中点,故OM⊥BC,
![]() 又∵∠BAC=900 ,∴
又∵∠BAC=900 ,∴![]()
∵![]() ,∴
,∴![]()
即: 42=(x2+y2)+[(x-0)2+(y-0)2]
化简为x2+y2-2y-6=0,即x2+(y-1)2=7.
∴所求轨迹为以(0,1)为圆心,以![]() 为半径的圆。
为半径的圆。
10、(1)求证:曲线C与直线l相切的条件是(a-2)(b-2)=2 ;
(2)求ΔAOB面积的最小值。
解:(1)直线l的方程为![]()
即bx+ay-ab=0
圆心O到直线l的距离d= ,
,
当d=1时,直线与圆相切,
即 =1
=1
整理得(a-2)(b-2)=2
所以曲线C与直线l相切的条件是(a-2)(b-2)=2.
(2)![]()
当且仅当a=2+![]() 时等号成立.
时等号成立.
第6课时 直线和圆的位置关系测试卷
一、选择题(每小题5分,共60分)
1、设点A(-1,2),B(2,-2),C(0,3),且点M(a,b)(a![]() 0)是线段AB上一点,则直线MC的斜率k的取值范围是( )
0)是线段AB上一点,则直线MC的斜率k的取值范围是( )
A . [![]() B.[-1,
B.[-1,![]() C. [
C. [![]() D.(-
D.(-![]()
2、若直线2x-3y+6=0绕它与y轴的交点逆时针旋转450角,则此时在x
轴上的截距是 ( )
A. ![]() B.
B. ![]() C. -
C. -![]() D.
D. ![]()
3、如果直线沿x轴负方向平移3个单位,再沿y轴正方向平移1个单位后,又回到原来的位置,那么直线l的斜率是( )
A. -![]() B. -3 C.
B. -3 C. ![]() D . 3
D . 3
4、![]() ABC的三个顶点为A(4,1),B(-1,-6),C(-3,2),R为这个三角形三边围成的区域(包括边界),当P(x,y)在R中变动时,S=4x-3y的最大值及最小值为( )
ABC的三个顶点为A(4,1),B(-1,-6),C(-3,2),R为这个三角形三边围成的区域(包括边界),当P(x,y)在R中变动时,S=4x-3y的最大值及最小值为( )
A. 14和-18 B. 18和-14 C.13和-18 D. 14和-13
5、如果直线l1,l2的斜率为k1,k2,二直线的夹角为![]() ,若k1,k2分别为二次方程x2-4x+1=0的两根,那么
,若k1,k2分别为二次方程x2-4x+1=0的两根,那么![]() 为( )
为( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
6、直线4x-3y-2=0与圆x2+y2-2ax+4y+a2-12=0总有两个交点,则a应满足( )
A.-3<a<7 B.-6<a<4 C.-7<a<3 D. -21<a<19
7、若直线ax+by-3=0与圆 x2+y2+4x-1=0切于点P(-1,2),则ab的积为( )
A. 3 B. 2 C.-3 D. -2
8、过Q(2,3)引直线与圆x2+y2+8x+2y+8=0交于R,S两点,那么弦RS的中点的轨迹为( )
A.圆(x+1)2+(y-1)2=![]() B.圆x2+y2+2x-2y
B.圆x2+y2+2x-2y![]() =0的一段弧
=0的一段弧
C.圆x2+y2+2x-2y-11=0的一段弧 D. 圆(x+1)2+(y-1)2=13
9、两圆外切于P,AB是它们的一条公切线(切点为A,B),若![]() PAB的周长为40,面积为60,则点P到AB的距离为( )
PAB的周长为40,面积为60,则点P到AB的距离为( )
A. ![]() B.
B.![]() C.
C. ![]() D. 17
D. 17
10、在圆x2+y2-5x=0内,过点(![]() )有n条长度成等到差数列的弦,最小弦长为a,最大弦长为an.若公差d
)有n条长度成等到差数列的弦,最小弦长为a,最大弦长为an.若公差d![]() ,那么n的取值集合是( )
,那么n的取值集合是( )
A.{3,4,5} B.{4,5,6,7} C. {3,4,5,6} D. {5,6,7,8}
11、若圆C1:(x-a)2+(y-b)2=b2+1始终平分圆C2: (x+1)2+(y+1)2=4的周长,则实数a,b应满足的关系式是( )
A. a2-2a-2b-3=0 B. a2+2a+2b+5=0
C.a2+2b2+2a+2b+1=0 D. 3a2+2b2+2a+2b+1=0
12、直线![]() 截圆x2+y2=4得劣弧对的圆心角为( )
截圆x2+y2=4得劣弧对的圆心角为( )
A.
![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二、填空(每小题4分,共20分)
13、由方程x2+xy-6y2=0所确定的两条直线的夹角为
14、若动点A(x1,y1),B(x2,y2)分别在直线l1:x+y-7=0和l2:x+y-5=0上移动,则AB的中点M到原点的距离的最小值为
15、设P(x,y)为圆x2+(y-1)2=1上任意一点,欲使不等式x+y+m![]() 恒成立,则m的取值范围是
.
恒成立,则m的取值范围是
.
16、圆C:(x-cos![]() )2+(y-sin
)2+(y-sin![]() )2=25与直线l:(2m+1)x+(m+1)y-7m-4=0(m
)2=25与直线l:(2m+1)x+(m+1)y-7m-4=0(m![]() R)的位置关系是
R)的位置关系是
三、解答题(本大题共6小题,共74分。解答应写出文字说明、证明过程或推演步骤)
17、(12分)过点P(3,0)作直线l与两直线l1:2x-y-2=0,l2:x+y+3=0分别相交于A、B两点,且P平分线段AB,求直线的方程。
18、(12分)已知圆心在直线2x+y=0上,且过点A(2,-1),与直线x-y-1=0相切,求圆的方程。
19、(12分)已知x2+y2=9的内接△ABC中,点A的坐标是(-3,0),重心G的坐标是(![]() ,求(1)直线BC的方程;(2)弦BC的长度.
,求(1)直线BC的方程;(2)弦BC的长度.
20、(12分)已知直线l:y=k(x+2![]() 与圆O:x2+y2=4相交于A,B两点,O为坐标原点,△AOB的面积为S。(1)试将S表示为k的函数S(k),并求出它的义域;求S的最大值,并求出此时的k值。
与圆O:x2+y2=4相交于A,B两点,O为坐标原点,△AOB的面积为S。(1)试将S表示为k的函数S(k),并求出它的义域;求S的最大值,并求出此时的k值。
21、(12分)李明同学准备用100元买空白磁盘和空白光碟,已知空白磁盘售价为4元/张,空白光碟的售价7元/张,问李明同学怎样设计购买方案,才能达到磁盘、光碟都买并且都不超过10张,而又使剩下的钱最少。
22、(14分)当m为参数时,集合A={(x,y)∣x2+y2+x-6y+m=0}是以(-![]() ,3)为圆心的同心圆系,问m取何值时,直线x+2y-3=0与圆系中的某一个圆交于P,Q两点,满足条件OP⊥OQ(O为坐标原点).
,3)为圆心的同心圆系,问m取何值时,直线x+2y-3=0与圆系中的某一个圆交于P,Q两点,满足条件OP⊥OQ(O为坐标原点).
选择题:1、D 2、B 3、A 4、C 5、A 6、B 7、B 8、C
9、C 10、B 11、B 12、C
填空题:13、45 ;14.3![]() ; 15、
; 15、![]() ;16、相交.
;16、相交.
解答题:17解:设l与直线2x-y-2=0交于点A1(x1,y1),则l与直线x+y+3=0交于
点(6-x1,-y1), 由![]() 解得:x1=
解得:x1=![]() .
.
又由l经过P(3,0),A(![]() 得直线l的方程为8x-y-24=0.
得直线l的方程为8x-y-24=0.
18、解:由圆心在直线2x+y=0上,设圆心坐标为(x0,-2x0)∵过点A(2,-1)且与直线x-y-1=0相切,∴![]() ,解得x0=1或x0=9当x0=1时,半径r=
,解得x0=1或x0=9当x0=1时,半径r=![]() ,当x0=9时,半径r=
,当x0=9时,半径r=![]() ,
,
∴所求圆的方程为:(x-1)2+(y+2)2=2或(x-9)2+(y+18)2=338
19、解:设B(x1,y1),C(x2,y2),连AG交BC于M,则M为BC的中点,
由三角形的重心公式得: ,
,
∴点M的坐标为(![]() ,连结OM,则OM⊥BC,又kOM=-2,
∴kBC=
,连结OM,则OM⊥BC,又kOM=-2,
∴kBC=![]() 。∴BC的方程为y+
。∴BC的方程为y+![]() ,即4x-8y-15=0.
,即4x-8y-15=0.
(2)连结OB,在Rt△OB M中,
![]()
20、解:作OD⊥AB于D,
则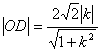 ,弦长
,弦长![]()
△
ABC的面积S=![]() .
.
![]()
(2)设∠AOB=![]() ,则
,则![]()
∴当![]() =900时,
=900时,![]() 此时
此时![]() .即
.即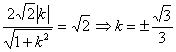
21、 解:设李明购买磁盘、光碟分别为、张,
则由题意知:
作出其表示的平面区域知其可行域内的整点(9,9)使u=4x+7y取得最大值99,此时余钱100-99=1最少,此时x=y=9,即李明应买光碟、磁盘各9张。
22、解:设P(x1,y1),Q(x2,y2),,则![]()
由OP⊥OQ,得![]() y2=0
y2=0
由![]() 消去y,得5x2+10x+4m-27=0 ①
消去y,得5x2+10x+4m-27=0 ①
∴x1+x2=-2, x1x2=![]() ②
②
而P,Q在直线x+2y-3=0上,则
y1y2=![]() (3-x1)(3-x2)=
(3-x1)(3-x2)=![]() [9-3(x1+x2)+x1x2]=
[9-3(x1+x2)+x1x2]=![]() ③
③
将②,③代入x1x2+y1y2=0解得m=3,将其代入①检验,⊿>0成立,故m=3为所求。