数学培训3
一、选择题：本大题共12小题，每小题5分，共60分。在每小题所给出的四个选项中，只有一个是符合题目要求的。
1、已知两点A（-2，m），B（m，4），直线AB斜率为-2，则m的值为（ ）
A、-8 B、0 C、4 D10
2、若a，b是任意实数，且a＞b，则
A、a2＞b2
B、
＞1
C、lg（a-b）＞0 D、（
）a＜（）b
3、下列命题正确的是（ ）
A、如果直线的倾斜角是α，则直线的斜率为tanα
B、方程
=1表示斜率为1，在y轴上截距为2的直线
C、ΔABC三个顶点坐标是A（0，3），B（-2，0），C（2，0），BC边中线的方程是x=0
D若直线L与直线3x+4y-5=0关于直线y=0对称，则直线L的倾斜角为arctan
4、如图，直线ax-y+b=0与圆x2+y2-ax+by=0的图象只能是（ ）
5、不等式
≥x的解集是（ ）
A、{x-1＜x＜2} B、{x-2≤x≤2} C、{x0≤x＜2} D、{xx≥0}
x=1+
cosθ
6、已知圆C： （θ为参数），直线L：x+y=b，若直线L与圆C相交于A，
y=1+sinθ
B两点，且AB=2，则b等于（ ）
A、2- B、2+
C、2±
D、其他情况
7、如果椭圆
=1上的点A到右焦点的距离等于4，那么点A到左准线距离是（ ）
A、
B、10
C、6
D、
8、若x-1＜
，y-2＜，则下列不等式一定成立的是（ ）
A、2x-y＜ε B、2x-y＞ε C、2x-y＞
ε D、2x-y＜ε
9、椭圆
=1上的点P到焦点F1的距离为2，N是PF1的中点，则ON的值为（ ）
A、4
B、2
C、8
D
10、过点P（2，1）做圆C：x2+y2-ax+2ay+2a+1=0的切线有两条，则a取值范围是（ ）
A、a＞-3 B、a＜-3 C、-3＜a＜-
D、-3＜a＜-或a＞2
11、短轴长为
，离心率e=的椭圆两焦点为F1，F2，过F1作直线交椭圆于A，B两点，则ΔABF的周长为（ ）
A、3 B、6 C、12 D、24
12、一批长3000mm的条形钢材，需要将其截成长400mm和800mm的两种毛坯，则钢材的最大利用率为（ ）
A、93.52% B、93.33% C、94.15% D、93.13%
二、填空题：本题共4小题，每小题4分，共16分。把答案填在横线上。
13、若直线（2m2+m-3）x+（m2-m）y=4m-1与直线2x-3y=5平行，则m= 。
14、2003年10月15日，我国发射的神州五号截人飞船的运动轨道是以地心（地球的中心）F2为一个焦点的椭圆。已知它的近地点A（离地面最近的点）距地面200km，远地点B（离地面最远的点）距地面350km，并且F2、A、B在同一直线上，地球半径为6371km。则神州五号载人飞船的运行轨迹方程为 。（以AB所在直线为x轴，线段AB的中垂线为y轴，建立直角坐标系）
15、已知a＞0，b＞0，且
+
=1，则a+b的最小值为
。
16、若关于x的方程
=2x+b有且只有一个实数解，则b值为
。
三、解答题：本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。
17、解不等式：
≤7
18、已知ΔABC的两条高线所在的直线方程为x+y=0，2x-3y+1=0，并且点A（1，2）
求（1）直线BC的方程；（2）内角A的大小。
19、已知ΔABC的顶点B（0，0），C（5，0），AB边上的中线长为CD=3，求顶点A的轨迹方程。
20、已知a、b∈R+，a+b=1 求证：
≤
+
＜
21、在某沙漠地带，考察车每天行驶200km，每辆考察车可以装载供行驶14天的汽油。现有5辆考察车，同时从驻地A出发，计划完成任务后，再沿原路返回驻地。为了让其中3辆尽可能向更远的地方进行考察（然后再一起返回），甲、乙两车行至B处，仅留足自己返回驻地所需汽油，将多余的汽油供另外3辆使用。问其他3辆可以行进的最远路程（从A到最远处的单程）是多少？
22、已知椭圆的一个顶点为A（0，-1），焦点在x轴上，其右焦点到直线x-y+2=0的距离为3。（1）求椭圆的方程；
（2）椭圆与直线y=kx+m（k≠0）相交于不同的两点M，N。当AM+AN时，求m取值范围。
数学培训（3）参考答案
一、选择题
1A 2D 3D 4C 5B 6C 7B 8A 9A 10D 11B 12B
二、填空题
13、-
14、
=1
15、16
16、-≤b≤1或b=
三、解答题
17、解：原不等式可以整理为
≤0 即
≥0
有序轴法的原不等式的解集为{xx≥
或x≤4}
18、解：（1）易知，两条高线所在直线都不过点A，
所以不妨设AC边上的高所在的直线方程为x+y=0，
AB边上的高所在的直线方程2x-3y+1=0，
则AC所在直线方程y-2=1（x-1），即x-y+1=0；
AB所在直线方程为y-2=-（x-1），即3x+2y-7=0
x+y=0
解方程组 得B（7，-7）
3x+2y-7=0
x-y+1=0
解方程组 得C（-2，-1）
2x-3y+1=0
所以直线BC的方程为2x+3y+7=0
（2）∠A是直线AC到直线AB的角，因为kAC=1，kAB=-
所以tanA=
=5
又A∈（0，π），
所以∠A=arctan5。
19、解：设A（x，y），D（x′，y′），
则x=2x′，y=2y′，即x′=
，y′=
又由CD=3得（x′-5）2+y′2=9
所以（-5）2+（）2=9
即（x-10）2+y2=36 （y≠0）为所求轨迹方程。
20、解：
=
=
因为a、b∈R+，a+b=1，所以a+b=1≥2
，所以0≤ab≤
所以2≤ab+2≤+2，所以
≤≤
即≤＜
21、解：设考察车到中途B处用了x天，从B到最远处用了y天，
则2[3（x+y）+2x]=14×5，即5x+3y=35
由题意有x＞0，y＞0，又14×5-（5+2）x≤14×3，即x≥4
5x+3y=35
所以问题转化为在线形约束条件 x≥4 下，求y+x的最大值，
y＞0
易知y=5，此时x=4
这样，其他3辆车可以行进的最远距离为200×（4+5）=1800（km）
22、解：（1）由已知设椭圆方程为
=1（a＞b＞0），其中b=1，设右焦点为（c，0），则
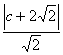=3，解得c=，所以a=，所以椭圆方程为
+y2=1
y=kx+m
（2）设P为MN的中点，解方程组
x2+3y2-3=0
得（3k2+1）x2+6mkx+3（m2-1）=0
因为相交两点，所以△=-12m2+36k2+12＞0，得m2＜3k2+1
xM+xN=
xP=
所以yP=kxP+m=
所以kAP=
由MN⊥AP得=-
即得2m=3k2+1代入m2＜3k2+1得0＜m＜2，
又由2m=3k2+1的k2=
得m＞
综上＜m＜2为所求。