数学培训3
第一部分：
1、à已知两点A（-2，m），B（m，4），直线AB斜率为-2，则m的值为（ ）
A、-8 B、0 C、4 D10
2、à若a，b是任意实数，且a＞b，则
A、a2＞b2 B、
＞1
C、lg（a-b）＞0 D、（
）a＜（
）b
3、--à>下列命题正确的是（ ）
A、如果直线的倾斜角是α，则直线的斜率为tanα
B、方程
=1表示斜率为1，在y轴上截距为2的直线
C、ΔABC三个顶点坐标是A（0，3），B（-2，0），C（2，0），BC边中线的方程是x=0
D若直线L与直线3x+4y-5=0关于直线y=0对称，则直线L的倾斜角为arctan
4、--à>如图，直线ax-y+b=0与圆x2+y2-ax+by=0的图象只能是（ ）
5、--à>不等式
≥x的解集是（ ）
A、{x-1＜x＜2} B、{x-2≤x≤2} C、{x0≤x＜2＝ D、{xx≥0}
6、--à>已知圆C：
y=1+
sinθ
x=1+
cosθ（θ为参数），直线L：x+y=b，若直线L与圆C相交于A，
B两点，且AB=2，则b等于（ ）
A、2-
B、2+
C、2± D、其他情况
7、--à>如果椭圆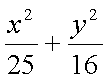
=1上的点A到右焦点的距离等于4，那么点A到左准线距离是（ ）
A、
B、10
C、6
D、
8、--à>若x-1＜
，y-2＜
，则下列不等式一定成立的是（ ）
A、2x-y＜ε B、2x-y＞ε
C、2x-y＞
ε D、2x-y＜ε
9、--à>椭圆
=1上的点P到焦点F1的距离为2，N是PF1的中点，则ON的值为（ ）
A、4 B、2 C、8 D
10、--à>过点P（2，1）做圆C：x2+y2-ax+2ay+2a+1=0的切线有两条，则a取值范围是（ ）
A、a＞-3 B、a＜-3 C、-3＜a＜-
D、-3＜a＜-
或a＞2
11、--à>短轴长为
，离心率e=
的椭圆两焦点为F1，F2，过F1作直线交椭圆于A，B两点，则ΔABF2的周长为（
）
A、3 B、6 C、12 D、24
12、--à>一批长3000mm的条形钢材，需要将其截成长400mm和800mm的两种毛坯，则钢材的最大利用率为（ ）
A、93.52% B、93.33%
C、94.15% D、93.13%
第二部分：
13、~.~若直线（2m2+m-3）x+（m2-m）y=4m-1与直线2x-3y=5平行，则m= 。
14、~.~2003年10月15日，我国发射的神州五号截人飞船的运动轨道是以地心（地球的中心）F2为一个焦点的椭圆。已知它的近地点A（离地面最近的点）距地面200km，远地点B（离地面最远的点）距地面350km，并且F2、A、B在同一直线上，地球半径为6371km。则神州五号载人飞船的运行轨迹方程为 。（以AB所在直线为x轴，线段AB的中垂线为y轴，建立直角坐标系）
15、~.~已知a＞0，b＞0，且
+
=1，则a+b的最小值为
。
16、~.~若关于x的方程
=2x+b有且只有一个实数解，则b值为
。
第三部分:
17、~.~解不等式：
≤7
18、~.~已知ΔABC的两条高线所在的直线方程为x+y=0，2x-3y+1=0，并且点A（1，2）
求（1）直线BC的方程；（2）内角A的大小。
19、~.~已知ΔABC的顶点B（0，0），C（5，0），AB边上的中线长为CD=3，求顶点A的轨迹方程。
20、~.~已知a、b∈R+，a+b=1 求证：
≤
+
＜
21、~.~在某沙漠地带，考察车每天行驶200km，每辆考察车可以装载供行驶14天的汽油。现有5辆考察车，同时从驻地A出发，计划完成任务后，再沿原路返回驻地。为了让其中3辆尽可能向更远的地方进行考察（然后再一起返回），甲、乙两车行至B处，仅留足自己返回驻地所需汽油，将多余的汽油供另外3辆使用。问其他3辆可以行进的最远路程（从A到最远处的单程）是多少？
22、~.~已知椭圆的一个顶点为A（0，-1），焦点在x轴上，其右焦点到直线x-y+2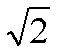
=0的距离为3。
（1）求椭圆的方程；
（2）椭圆与直线y=kx+m（k≠0）相交于不同的两点M，N。当AM+AN时，求m取值范围。