数学培训5
一、选择题(本大题共15小题,每小题3分,共45分,在每小题给出的四个选项中,只有一项符合题目要求,请将正确答案填入下表内)
1、设a,b,c,d![]() R,且a>b,c >d,则下列结论中正确的是
R,且a>b,c >d,则下列结论中正确的是
A. a+c>b+d
B. a-c>b-d C. ac>bd D.![]()
2、若直线l的倾斜角为![]() ,则它的一个方向向量为
,则它的一个方向向量为
A. (-1,![]() )
B.(1,
)
B.(1,![]() ) C. (
) C. (![]() ,1)
D. (3
,1)
D. (3![]() ,1)
,1)
3、直线ax+2y+2=0与直线3x-y-2=0平行,则实数a的值为
A. –3 B. –6
C.-![]() D.
D.![]()
4、不等式![]() <1的解集为
<1的解集为
A. ﹛x︱-1<x<![]() ﹜
B. {x︱-1<x<1或 x>
﹜
B. {x︱-1<x<1或 x>![]() }
}
C. {x︱-![]() <x<-1或1<x<
<x<-1或1<x<![]() }
D.{x︱x<1或1<x<
}
D.{x︱x<1或1<x<![]() }
}
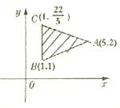 5、给出平面区域如图,若使目标函数z=ax+y(a>0)取得最大值
5、给出平面区域如图,若使目标函数z=ax+y(a>0)取得最大值
的最优解有无穷多个,则a的值为
A. ![]() B.
B.
![]()
C. 4
D.![]()
6、已知非零实数a、b、c满足︱a-c︱<︱b︱,则下列不等式成立的是
A. a<b+c B. a>c-b C. ︱a︱<︱b︱+︱c︱ D. ︱a︱>︱b︱-︱c︱
7、椭圆![]() =1的准线方程是
=1的准线方程是
A. x=±![]() B. y=±
B. y=±![]() C.
x=±
C.
x=±![]() D. y=±
D. y=±![]()
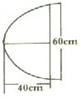 8、如图,拧照灯反射镜的纵断面是抛物线的一部分光源在抛物线的焦点,已知灯口直径是60cm,灯深40cm,那么光源到反射镜顶点距离是
8、如图,拧照灯反射镜的纵断面是抛物线的一部分光源在抛物线的焦点,已知灯口直径是60cm,灯深40cm,那么光源到反射镜顶点距离是
A. 11.25cm B. 5.625 cm C. 20 cm D. 10 cm
9、双曲线的焦距是准线间距离的4倍,则此双曲的离心率e等于
A. ![]() B.
2
C. 3
D. 4
B.
2
C. 3
D. 4
10、如果双曲线![]() =1上一点P到它的右焦点的距离是8,那么P到它的右准线距离是
=1上一点P到它的右焦点的距离是8,那么P到它的右准线距离是
A. 10 B. ![]() C. 2
C. 2![]() D.
D. ![]()
11、焦点为(0,6)且与双曲线![]() 有相同渐近线的双曲线方程为
有相同渐近线的双曲线方程为
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
12、已知圆C:![]() =1,点A(-2,0)及点B(2,a),从A点观察B点要使视线不被圆C挡住,则a的取值范围是
=1,点A(-2,0)及点B(2,a),从A点观察B点要使视线不被圆C挡住,则a的取值范围是
A. (-∞,-1)∪(1,+∞) B. (-∞,-2)∪(2,+∞)
C. (-∞,-4)∪(4,+∞)
D. (-∞,-![]() )∪(
)∪(![]() ,+∞)
,+∞)
13、将一张画了直角坐标系且两轴的长度单位相同的纸折叠一次,使点(2,0)与点(-2,4)重合,若点(7,3)与点(m,n)重合,则m+n的值为
A. 4 B. –4 C. 10 D. –10
14、某工厂第一年产量为A,第二年的增长率为a,第三年的增长率为b ,这两年的年平均增长率为x,则
A. x=![]() B. x≤
B. x≤![]() C. x>
C. x>![]() D. x≥
D. x≥![]()
15、买4枝郁金香和5枝丁香的金额和小于22元,而买6枝郁金香和3枝丁香的金额和大于24元,那么买2枝郁金香和买3枝丁香的金额比较,其结果是
A. 2枝郁金香贵 B. 3枝丁香贵 C. 相同 D. 不能确定
二、填空题(本大题共5小题,每小题3分,共15分,请把答案填在题中的横线上)
16、椭圆![]() 的一个焦点为(0,5),则m=___________________________.
的一个焦点为(0,5),则m=___________________________.
17、不等式x2+ax+b<0的解集为{x︱-1<x<2},则直线ax+by+1=0的斜率k=______________________.
18、圆(x-3)2+(y-4) 2=1上的点到直线3x+4y-10=0的最短距离是_________________.
19、已知抛物线的顶点在原点,焦点在x轴上,抛物线上一点A(-3,a)到焦点距离为5,则a=____________________.
20、给出下列曲线:①4x+2y-1=0;②x2+y2=3;③![]() + y2=1;④
+ y2=1;④![]() -y2=1其中与直线y=-2x-3有交点的曲线方程为_________________________(写出所有满足条件的序号)
-y2=1其中与直线y=-2x-3有交点的曲线方程为_________________________(写出所有满足条件的序号)
三、解答题(本大题共5小题,共40分,解答应写出文字说明、证明过程演算步聚)
![]() x2+4x-5>0,
x2+4x-5>0,
21、(本小题满分8分)解关于x的不等式
![]() .
.
22、(本小题满分6分)设A、B两点的坐标分别是(1,0)(-1,0),若KAM·KMB=-1求动点M的轨迹方程。
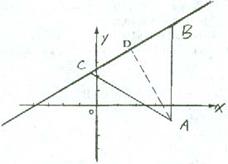
23、(本小题满分8分)正三角形ABC顶点A的坐标为(4,-1),一条边所在的直线方程为x-![]() y+4=0,求另两条边所在直线方程。
y+4=0,求另两条边所在直线方程。
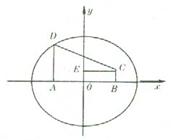
24、(本小题满分10分)如图,直角梯形ABCDK中∠DAB=90°,AD∥BC,AB=2,AD=![]() ,BC=
,BC=![]() .椭圆P以AB为焦点且经过点D。
.椭圆P以AB为焦点且经过点D。
|
|
(2)若点E满足EC=![]() AB,问是否存在不平行于AB的直线l与椭圆P交于M、N两点且︱ME︱=︱NE︱。若存在,求出直线?与AB夹角的范围。若不存在,说明理由。
AB,问是否存在不平行于AB的直线l与椭圆P交于M、N两点且︱ME︱=︱NE︱。若存在,求出直线?与AB夹角的范围。若不存在,说明理由。

25、(本小题满分8分)现有A、B、C、D四个长方体容器,A、B的底面积均为x2,高分别为x、y;C、D的底面积均为y2,高也分别为x、y(其中x≠y),现规定一种两人的游戏规则:每人从四种容器中取两个盛水,盛水多者为胜,问先取者未能确定x与y大小的情况下有没有必胜的方案?若有的话,有几种?
数学培训5参考答案
一、选择题(3×15=45分)
A A B C B C D B B D D D C B A
二、填空题:(3×5=15分)
16、54 17、-![]() 18、2 19、±2
18、2 19、±2![]() 20、②、③、④
20、②、③、④
三、解答题
21、解:由x2+4x-5>0得 (x+5)(x-1)>0,∴x>1akg x<-5………………2分
由![]() 得
得 ![]() -2>0,
-2>0,
∴![]() >0, ∴1<x<5.………………………………………………………7分
>0, ∴1<x<5.………………………………………………………7分
∴原不等式的解集为{x︱1<x<5}.……………………………………………8分
22、解:设M(x,y),则
KAM=![]() ,KBM=
,KBM=![]() .………………………………………………………2分
.………………………………………………………2分
由KAM·KBM=-1得:
![]() ·
·![]() =-1,
=-1,
∴x2+y2=1,……………………………………………………………………4分
显然x≠±1,…………………………………………………………………5[admin1] 分
∴所求M点的轨迹方程为x2+y2=1(x≠±1)………………………………6分
23、解:∵(4,-1)不满足方程x-![]() y+4=0,…………………………1分
y+4=0,…………………………1分
 ∴BC所在直线方程为x-
∴BC所在直线方程为x-![]() y+4=0,……………………………………2分
y+4=0,……………………………………2分
∴KAD=- ,……………………………………………3分
,……………………………………………3分
∴AD的倾斜角为120°,……………………………………………………4分
∴AB和AC的倾斜角度分别为90°和150°………………………………6分
∴AB所在直线方程为x=4……………………………………………………7分
AC所在直线议程为y=-![]() (x-4)-1即x+
(x-4)-1即x+![]() =0……………8分
=0……………8分
24、解:(1)如图以AB所在直线为x轴,AB中垂线为y轴建立直角坐标系。
则:A (-1,0) B (1,0) C (1,![]() ) D(-1,
) D(-1,![]() ).
).
设椭圆方程为![]()
由题意得2a=︱DA︱+︱DB︱=![]() =4 则a=2,∵c=1,∴b2=3
=4 则a=2,∵c=1,∴b2=3
|
|
 (2)∵EC=
(2)∵EC=![]() AB,∴l⊥AB不符。
AB,∴l⊥AB不符。
∴设l=y=kx+m(k≠0),M(x1,y1),N(x2,y2),MN中点F(x0,y0)
![]() y=kx+m,
y=kx+m,
由 →(3+4k2)x2+8kmx+4m2-12=0
![]()
![]() △=64k2m2-4(3+4k2)(4m2-12)>0,
△=64k2m2-4(3+4k2)(4m2-12)>0,
则
x1+x2=-![]() , y0=kx0+m=
, y0=kx0+m=![]() .
.
解得 4k2+3≥m2 (*).……………………6分
![]() . ∵∣ME∣=∣NE∣,∴MN⊥EF.
. ∵∣ME∣=∣NE∣,∴MN⊥EF.
∴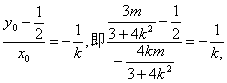
∴m=![]() 代入(*)得,
代入(*)得,
3+4k2≥![]() , ∴3+4k2≤4, 即4k2≤1 ∴-
, ∴3+4k2≤4, 即4k2≤1 ∴-![]() ≤k≤
≤k≤![]() 且k≠0.……9分
且k≠0.……9分
∴l与AB的夹角范围是(0,arc
tan ![]() ).…………………………………………………10分
).…………………………………………………10分
25.解:依题意可知A、B、C、D四个容器的容积分别为x3,xy2,xy2,y3.…………1分
按照游戏规则,先取者只有三种不同的到法:
①取A,B;②取A,C;③取A,D ………………………………………………2分
问题的实质是比较容积两两和的大小。
①若先取A、B,则后取者只能取C、D,
∵(x3+xy2)-(x2y+y3)=x(x2+y2)-y(x2+y2)=(x-y)(x+y)2,
显然,(x+y)2>0,而x与y的大小不确定,
∴(x-y)(x+y) (x+y)2的正负不能确定。
即x3+x2y与xy2+y3有大小不定,这种取法无必胜的把握。…………………………4分
②若先取A、C,则后取者只能了B、D,
∵(x3+xy2)-(x2y+y3)=x(x2+y2)-y(x2+y2)=(x-y)(x2+y2),
∴类似于①的分析知,这种取法也无必胜的把握。………………………………6分
③若先取A、D,则后取者只能取B、C,
∵(x3+y3)-(x2y+xy2)
=(x+y)(x2-xy+y2)-xy(x+y)=(x+y)(x2-2xy+y2)=(x+y)(x-y) 2.
又x≠y,x>0,y>0, ∴(x+y)(x-y) 2>0,
即x3+y3>x2y+xy2,故先取A、D是唯一必胜的方案。………………………………8分
[admin1]