高二上学期期中测试
数 学 试 卷
注意：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选题）两部分，共120分，考试时间120分钟。
第Ⅰ卷（选择题共48分）
一、选择题（每题有四个选项，只有一个是正确的，请把答案涂在答题卡上，共12个小题，
每小题4分）
1．若a、b为实数，则ab（a－b）> 0成立的一个充要条件是 （ ）
A．a < 0 < b B．b < a < 0 C．a > b > 0 D． 
< 
2．下列各式中最小值是2的是 （ ）
A．
＋
B．
C．tanx＋cotx D．
3．若a－c< b ,则下列不等式不成立的是 （ ）
A．a<b＋c B．c<a＋b C．b>c－a D．b<a－c
4．直线L1:2x＋(ｍ＋１)ｙ＋４＝０与直线Ｌ２：ｍｘ＋3y－2=0平行，则ｍ的值为（ ）
A．2 B．－3 C．2或－3 D．－2或－3
5．直线2x－y－4=0绕它与x轴的交点逆时针旋转
后,所得的直线方程为 （ ）
A．x－3y－2=0 B．3x＋y－6=0 C． 3x－y＋6=0 D．x＋y－2=0
6．直线x＋y－1=0到直线xsinα＋ycosα－1=0 (<α<
)的角是 （ ）
A．α－ B．－α C．α－
D．
－α
7．已知直线L1：2x－y＋3=0和直线L2：x－y＋2=0，若L2上任意一点到L1的距离与它到L
的距离相等，则直线L的方程是 （ ）
A．x－2y＋3=0 B．x－2y－3=0 C．x＋2y－1=0 D．y－1=
(x＋1)
8．不等式
< x＋1的解集是 （ ）
A．{xx >
-3} B．{x
< x < 
}
C．{xx <
1} D．{xx >
或－<x<1}
9．不等式x－1＋x＋2≤a的解集非空,则实数a的取值范围是 （ ）
A．a>3 B．a≥3 C．a≤4 D． a≥4
10．已知直线y=
x＋b与曲线xy=相交于A、B两点，若∣AB∣=5，则实数b的值为
（ ）
A．±
B．
C． ± D．±
11．已知正数x,y满足x＋2y =1,则
＋
的最小值为 （ ）
A．3＋2 B．4＋ C．4 D．2＋3
12．△ABC中，a、b、c是内角A、B、C的对边，且lgsinA、lgsinB、lgsinC成等差数列，
则下列两条直线L1：（sin2A）x＋（sinA）y－a=0，L2：（sin2B）x＋（sinC）y－c =0的
位置关系是
A．重合 B．相交 C．垂直 D．平行
第Ⅱ卷（非选择题,共72分）
二、填空题(本大题共4个小题,每小题4分,满分16分)
13．若0≤x≤1,-1≤y≤2,则z=x＋4y的最小值为__________________.
14．已知A(-1,0),B(2,4), △ABC的面积为10,则动点C的轨迹方程是________________.
15．给出下列命题：
(1)线性规划中最优解指的是使目标函数取得最大值或最小值的变量x或y的值.
(2)线性规划中最优解指的是目标函数的最大值或最小值.
(3)线性规划中最优解指的是目标函数取得最大值或最小值的可行域.
(4)线性规划中最优解指的是使目标函数取得最大值或最小值的可行解.
其中正确的命题的题号是__________________.
16．已知关于x的不等式(a＋b)x＋(2a－3b)< 0的解集是(－∞,
) , 则关于x的不等式
(a－3b)x＋(b－2a)> 0的解集是_________________.
三、解答题(本大题共5个小题,满分56分,解答题应写出文字说明,证明过程或演算步骤)
17．(本小题满分10分) C
如图已知△ABC的底边AB长是6,并且∠B=2∠A,求顶点C的
轨迹方程.
B A
18．(本小题满分11分)
已知ΔABC的三边方程是AB：5x－y－12=0，BC：x＋3y＋4=0，CA：x－5y＋12=0，
求：
（1）∠A的大小。
（2）∠A的平分线所在的直线方程。
（3）BC边上的高所在的直线的方程。
19．(本小题满分11分)
设函数的集合S=｛f(x)｝，其中每个函数f(x)满足条件:当x1≤1、x2≤1时，f(x1)－f(x2)
≤4x1－x2,试判断g(x)=x2＋2x＋3是否属于S.
20．(本小题满分12分)
某种设备购买时费用为10万元,每年的设备管理费共计9千元,这种生产设备的维修费各年为:第一年2千元, 第二年4千元, 第三年6千元,而且以后以每年2千元的增量逐年递增.问这种生产设备最多使用多少年报废最合算(即使用多少年的年平均费用最少)?
21．(本小题满分12分)
已知n条直线：L1：x－y＋C1=0、 C1 =， L2：x－y＋C2=0，L3：x－y＋C3=0，
……Ln：x－y＋Cn=0 .(其中C1< C2 <C3 <……< Cn)这ｎ条平行线中，每相邻两条之间的
距离顺次为2，3，4，……，n.
(1)求Cn 。
(2)求x－y＋Cn=0与x轴、y轴围成的图形的面积。
(3)求x－y＋Cn-1=0与x－y＋Cn=0及x轴、y轴围成的图形的面积。
高二上学期期中试卷
数学试题答案
一、选择题：DDDCB DADBC AA
二、填空题: 13.－4 14. 4x－3y－16=0或4x－3y＋24=0 15.(4) 16. (－∞,－3)
三、解答题:
17．解:以直线AB为x轴,线段AB的中点为原点建立直角坐标系,则B(－3,0),A(3,0)
设点C的坐标为(x,y) ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．２分
当角Ｂ≠９００时:KBC=
,KAC=
因为∠B=2∠A所以有tanB=
,而当点C在x上方时:
tanB=KBC,tanA= －KAC, 当点C在x下方时: tanB=-KBC,tanA=KAC．．．．．．．．．．．．．5分
所以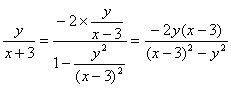
∵y≠0,∴
整理得:
3x2－6x－y2－9=0…………………………………………………………………8分
当角B=900时:∠A=450,点C的坐标为(-3,6)满足方程3x2-6x-y2-9=0
由题意可知C点必在y轴的左侧,所以所求方程为:
3x2-6x-y2-9=0(x<0且y≠0)……………………………………………………10分
18．解：(1)∵KAB=5，KAC=
∴tanA=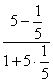
=
，∠A=arctan………………………………………3分
(2)由角平分线AD上任意一点到AC、AB的距离相等得：
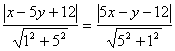，化简得：x+y-6=0或y=x由画图可知结果应为：
y = x ……………………………………………………………………………7分
(3)(过程略)BC边上的高AH所在的直线方程是:3x－y－6=0………………11分
19．解:设∣x1∣≤1，∣x2∣≤1，…………………………………………………2分
∣g（x1）－g（x2）∣=∣(x12－x22)＋2(x1－x2)∣
=∣x1－x2∣·∣x1＋x2＋2∣…………………………6分
≤∣x1－x2∣·(∣x1∣＋∣x2∣＋2)≤4∣x1－x2∣
所以g(x)∈S…………………………………………………………………11分
20．解:设使用x年的年平均费用为y万元.
由已知得:y=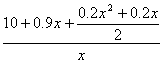
…………………………………………5分
即y=1＋
(x∈N＋)……………………………………………………………7分
由均值不等式知:y≥1+2
=3………………………………………………10分
当且仅当
=
即x=10时取等号
因此使用10年报废最合算,年平均费用为3万元…………………………………12分
21．解:(1)由题意可知:L1到Ln的距离为:
=2+3+4+……n,
∵
>∴=
…………………………………………………………4分
(2)设直线Ln:x－y＋cn=0交x轴于Ｍ点，交ｙ轴于Ｎ点，则△ＯＭＮ的面积为：
Ｓ△ＯＭＮ＝
│ＯＭ││ＯＮ│=
=
………………………………8分
（3）围成的图形是等腰梯形,由(2)知Ｓｎ＝．则有
Sｎ－１＝
Sｎ－Sｎ－１＝－＝ｎ３
所以所求面积为n3…………………………………………………………………12分