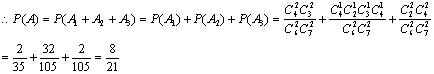高中学生学科素质训练
高二数学测试题—概率(7)
一、选择题(本大题共10小题,每小题5分,共50分)
1.盒子内有10个大小相同的小球,其中有6个红球,3个绿球和1个黄球,从中任意摸出1个球,则它不是红球的概率为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.把10本书随意地放在书架上,则其中指定的3本书放在一起的概率为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.有100件产品,其中有5件次品,从中有放回地连抽两次,则第二次才抽到合格品的概率为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.同时掷两颗骰子,得到的点数和为4的概率是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.某人投篮的命中率为![]() ,连续投篮5次,则“至少投中4次”的概率为 ( )
,连续投篮5次,则“至少投中4次”的概率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.10把钥匙中有3把能把门锁打开,住取2把能把门锁打开的概率为0.9、0.8、0.7,则没有一台机床需要工人照管的概率为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.一个工人看管三台机床,在一小时内,这三台机床需要工人照管的概率分别0.9、0.8、0.7,则没有一台机床需要工作照管的概率为 ( )
A.0.018 B.
8.摇奖器摇出的一组中奖号码为8,2,5,3,7,1。对奖票上的六个数字是从0,1,2,……,9这十个数字中任意选出六个不同数字组成的。如果对奖票上的六个数字中至少有五个与摇奖器摇出的号码相同(不计顺序)就可以得奖,则中奖的概率为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.在4次独立重复试验中,若随机事件A恰好发生一次的概率不大于其恰好发生两次的概率,则事件A在一次试验中发生的概率P的取值范围是 ( )
A.[0.4,1) B.(0,0.4]
C.(0,0.6] D.[0.6,1)
10.任意写一个无重复数字的三位数,其中十位上的数字最小的概率是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题(本大题共4小题,每小题6分,共24分)
11.有三部书,其中第一部有3卷,第二部有5卷,第三部有2卷,现将它们排成一排,每部书的各卷都排在一起的概率为 .
12.从5双鞋子中任取4只,则这4只鞋子中至少有2只可配成一双的概率为 .
13.6个人坐到9个座位的一排位置上,则恰有3个空位且3个空位互不相邻的概率为
.
14.一口袋中装有a只黑球,b只白球,它们大小相同,编号不同,现在把球随机地一只一只摸出来,则第k次摸出的球是黑球的概率为 .
三、解答题(本题共6题,共76分)
15.设有6个球,每个球都以同样的可能性落入10个格子的每一个格子中,
试求:(1)某指定的6个格子中各有一个球的概率.
(2)6个球各在一个格子中的概率.(12分)
16.某班组共有7名男生,4名女生,现要选出3人组成“环保宣传队”求随机选取3人至少有1名女生的概率?(12分)
17.甲乙两人独立地解决同一问题,若甲解决这个问题的概率为P1,乙解决这个问题的概率是P2,那么其中至少有一人解决这个问题的概率是多少?(12分)
18.将一枚硬币抛掷5次,
(1)求第二次,第五次出现反面,而另外三次都出现正面的概率;
(2)求二次出现反面,三次出现正面的概率.(12分)
19.某产品中有15只正品,5只次品,每次取1只测试,取后不放回,直到5只次品全部测出为止,求经过10次测试,5只次品全部被发现的概率。(14分)
20.有A、B两个袋子,A袋中装有4个白球、2个黑球,B袋中装有3个白球、4个黑球,从A、B两个袋子中各取2个球交换之后,求A袋中有4个白球的概率。(14分)
高二数学参考答案
(七)概率
一、选择题
1.B 2.C 3.C 4.B 5.A 6.C 7.B 8.D 9.A 10.A
二、填空题
11.![]()
12.![]()
13.![]()
14.![]()
三、解答题
15.解:这是古典概型问题
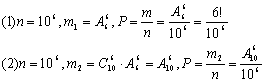
16.解:Ai={恰有I名女生},A={至少有一名女生},![]()
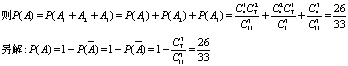
17:“至少有1人解决这个问题”的对立事件是“甲、乙都没有解决这个问题”其事件的概率为P=1-(1-P1)(1-P2)=P1+P2-P1P2
18.解:设Ai={第i次抛掷出现正面},则Ai![]() (i=1,2,……,5)相互独立且
(i=1,2,……,5)相互独立且
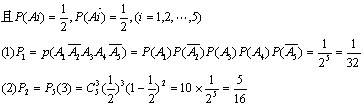
19.解:基本事件总数![]()
第5只次品在第10次测试时被发现,即前9次测试中恰好测到4只次品和5只正品,所以
![]()
20.解:设A={A袋中有4个白球},由于A袋中原来装有4个白球,白球数量未发生变化,故事件A由以下三个事件A1,A2,A3中至少有一个发生而发生.
A1={A袋中2个白球交换B袋中2个白球};
A2={A袋中1个白球1个黑球交换B袋中1个白球1个黑球};
A3={A3袋中2个黑球交换B袋中2个黑球};
A=A1+A2+A3
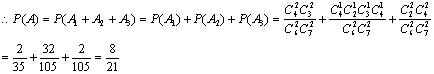
高二数学参考答案
(七)概率
一、选择题
1.B 2.C 3.C 4.B 5.A 6.C 7.B 8.D 9.A 10.A
二、填空题
11.![]()
12.![]()
13.![]()
14.![]()
三、解答题
15.解:这是古典概型问题
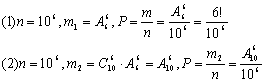
16.解:Ai={恰有I名女生},A={至少有一名女生},![]()
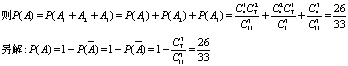
17:“至少有1人解决这个问题”的对立事件是“甲、乙都没有解决这个问题”其事件的概率为P=1-(1-P1)(1-P2)=P1+P2-P1P2
18.解:设Ai={第i次抛掷出现正面},则Ai![]() (i=1,2,……,5)相互独立且
(i=1,2,……,5)相互独立且
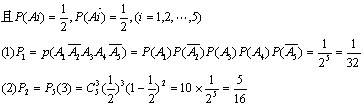
19.解:基本事件总数![]()
第5只次品在第10次测试时被发现,即前9次测试中恰好测到4只次品和5只正品,所以
![]()
20.解:设A={A袋中有4个白球},由于A袋中原来装有4个白球,白球数量未发生变化,故事件A由以下三个事件A1,A2,A3中至少有一个发生而发生.
A1={A袋中2个白球交换B袋中2个白球};
A2={A袋中1个白球1个黑球交换B袋中1个白球1个黑球};
A3={A3袋中2个黑球交换B袋中2个黑球};
A=A1+A2+A3