高中学生学科素质训练
高二数学测试题—平面的基本性质、两直线的位置关系(1)
一、选择题:(本大题共10小题,每小题5分,共50分)
1.三个互不重合的平面把空间分成六个部份时,它们的交线有 ( )
A.1条 B.2条 C.3条 D.1条或2条
2.两两相交的四条直线确定平面的个数最多的是 ( )
A.4个 B.5个 C.6个 D.8个
3.四条线段顺次首尾相连,它们最多可确定的平面个数有 ( )
A.4个 B.3个 C.2个 D.1个
4.在空间四点中,三点共线是四点共面的 ( )
A.充分必要条件 B.必要非充分条件
C.充分非必要条件 D.既非充分又非必要条件
5.若直线a、b异面,直线b、c异面,则a、c的位置关系是 ( )
A.异面直线 B.相交直线 C.平行直线 D.以上都有可能
6.正方体ABCD—A1B
A.2条 B.4条 C.5条 D.6条
7.在空间四边形ABCD的边AB、BC、CD、DA上分别取E、F、G、H四点如果EF与HG交于点M,则 ( )
A.M一定在直线AC上
B.M一定在直线BD上
C.M可能在AC上,也可能在BD上
D.M不在AC上,也不在BD上
8.在空间四边形ABCD中,M、N分别是AB、CD的中点,设BC+AD=
A.MN>a B.MN=a C.MN<a D.不能确定
9.“a、b是异面直线”是指:(1)![]()
且![]()
(5)不存在平面![]()
上述说法中,正确的是 ( )
A.(2)和(4) B.(2)和(5)
|
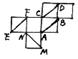
10.右图是一个正方体的展开图,在原正方体中,有下列命题:
①AB与CD所在直线垂直; ②CD与EF所在直线平行
③AB与MN所在直线成60°角; ④MN与EF所在直线异面
其中正确命题的序号是 ( )
A.①③ B.①④ C.②③ D.③④
二、填空题(本大题共4小题,每小题6分,共24分)
11.用一个平面去截正方体。其截面是一个多边形,则这个多边形的边数最多是
.
12.设平面![]() 则直线b和c是异面的充要条件是
则直线b和c是异面的充要条件是
.
13.若E、F、G、H顺次为空间四边形ABCD四条边AB、BC、CD、DA的中点,且EG=3,FH=4,则AC2+BD2= .
14.A、B是直线a上两点,直线b与a异面,C、D是直线b上两点,AB=8,CD=6,M、N是AD、BC的中点,且MN=5,则a,b所成的角为 .
|
15.已知:![]()
![]()
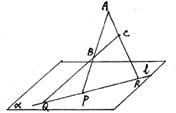
16.已知△ABC三边所在直线分别与平面α交于P、Q、R三点,求证:P、Q、R三点共线。(12分)
|
17.已知:平面![]()
求证:b、c是异面直线(12分)
|
|
|
(1)求证:MN是AB和PC的公垂线
(2)求异面二直线AB和PC之间的距离(14分)
高二数学参考答案
(一)平面的基本性质、两直线的位置关系
一、选择题
1.D 2.C 3.A 4.C 5.D 6.B 7.A 8.C 9.B 10.D
提示1、分类:1)当两个平面平行,第三个平面与它们相交时,有两条交线; 2)当三个平面交于一条直线时,有一条交线,故选D
2.∵平面ABC∩平面ACD=AC,先证M∈平面ABC,M∈平面ACD,从而M∈AC
二、填空题
11.6条 12.直线b、c和a都相交,但交点不同或直线b、c中有且仅有一条与a相交.
13.50 14.90°
三、解答题
15.本题主要考查用平面公理和推论证明共面问题的方法.
证明∵PQ∥a,∴PQ与a确定一个平面![]()
![]()
![]()
16.本题主要考查用平面公理和推论证明共线问题的方法
证明:∵A、B、C是不在同一直线上的三点
∴过A、B、C有一个平面![]()
又![]()
![]()
![]()
17.反证法:若b与c不是异面直线,则b∥c或b与c相交

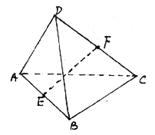
18.(本题考查中位线法求异面二直线所成角)
解:取BD中点M,连结EM、MF,则

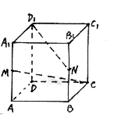
19.(本题考查平移法,补形法等求异面二直线所成角)
解:取DD1中点G,连结BG,MG,MB,GC得矩形MBCG,记MC∩BG=0
则BG和MC所成的角为异面直线CM与D1N所成的角.
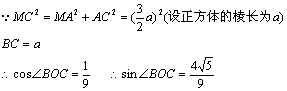
而CM与D1N所成角的正弦值为![]()
20.解:(1)连结AN,BN,∵△APC与△BPC是全等的正三角形,又N是PC的中点
∴AN=BN
又∵M是AB的中点,∴MN⊥AB
同理可证MN⊥PC
又∵MN∩AB=M,MN∩PC=N
∴MN是AB和PC的公垂线。
(2)在等腰在角形ANB中,![]()
即异面二直线AB和PC之间的距离为![]() .
.