高二第二学期期中试卷无答案

洞头一中2005学年高二第二学期期中试卷

数　 学

一、选择题：（本题有22小题，每小题2分，共44分）

1、　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  （　　 ）

A．　　　　　  B．　　　　  C．　　　　　  D．

2、直线的斜率为　　　　　　　　　　　　　　　　　　　　  （　　 ）

A．2　　　　　　　  B．1　　　　　　　 C．　　　　　  D．

3、下列函数为奇函数的是　　　　　　　　　　　　　　　　　  　　　　　　 （　　 ）

A．　　  B．　　　 C．　　　　D．

4、半径为3的球的体积等于　　　　　　　　　　　　　　　　　　　　　　　  （　　 ）

A．　　　　　　 B．　　　　　　 C．　　　　 D．

5、经过点A(2,1),且与直线y=x+1垂直的直线的方程为　　　　　　　　　　　 （　　 ）

A. y= x+3　　　　B. y= x-3　　　　　 C. y= -x-3　　　　 D. y= -x+3

6、抛物线的准线方程为　　　　　　　　　　　　　　　　　　　　　 （　　 ）

A．　　  B．　　　　 C．　　　 D．

7、从6位同学中挑选2位参加志愿者服务队，不同的挑选方法有　　　　　　　　 （　　 ）

A．30种　　　　　  B．15种　　 　　　C．10种　　　　D．5种

8、函数y=sinx的一个单调区间是　　　　　　　　　　　　　　　　　　　  （　　 ）

A、[]　　　　　 B、[]　　 C、[]　　　　　　 D、[]

9、不等式x-1≤1的解集是　　　　　　　　　　　　　　  　　　　　　　　 （　　 ）

 A、 　　　　　B、　[0，2]　　　 C、[-1，1]　　　 D、[-1，2]

10、已知、为两个单位向量，则一定有　　　　　　　　　　　　　　　　　  （　　 ）

A．=　　　 B．若//，则=　　  C．　　　 D．

11、为了得到函数的图象，只需把曲线上所有的点（　　 ）A．向右平行移动个单位长度　　　　　  B．向左平行移动个单位长度

C．向右平行移动个单位长度　　　　　  D．向左平行移动个单位长度

12、条件，条件，则p是q的　　　　　　　　　　　　  （　　 ）

A．充分而不必要条件　　　　　　　 B．必要而不充分条件　　　　　

C．充要条件　　　　　　　　　　　 D．既不充分也不必要条件

13、双曲线－=1的的渐近线方程是　　　　　　　　　　　　　　　　  （　　 ）

 A、y=±x　　　　　 B、y=±x　　　　 C、y=±x　　　　 D、y=±x

14、如图,在正四棱锥V-ABCD中,侧棱与底面边长相等,设二面角V-CD-A的平面角为α,则cosα=　　　　　　　　　　　　　　　　　　　  （　　 ）

  A、　　B、　　　　C、－ 　　 D、

15、若，则　 　　　　　　　　　　　 （　　 ）

A、　 B、　 C、　 D、

16、圆截轴所得的弦长为（　　 ）

A．10　　　　B．8　　　　C．6　　　　 D．4

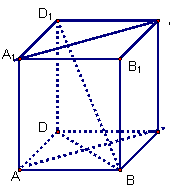
17、如图，已知正方体ABCD—A₁B₁C₁D₁，下列各组异面直线中，不互相垂直的是　　　　　　　　　　　　  （　　 ）

A．AA₁与BD₁　　　　 B．BD与A₁C₁　　

C．AC与BD₁　　　　  D．AD与BB₁

18、某单位“五 一”国际劳动节放假5天，安排甲、乙、丙、丁、戊5人值班，每人值1天，如果甲不能在第一天值班，也不能在最后一天值班，则不同的安排方案共有　　（　　 ）

A．54种　　　　　 B．72种　　　　　 C．90种　　　　  D．120种

19、如图，正四棱锥V—ABCD的侧棱与底面边长相等，则直线VA与平面VBD所成的角为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　 ）

A．　　　　  B．　　　　  C．　　　　 D．

A

O

F2

F1

B

x

y

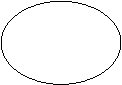
　　　　（第19题）　　　　　　　　　　　　　　　　　 （第21题）

20、在中，、、所对的边分别为、、，若，、分别是方程的两个根，则等于　　　　　　　　　　　　　　　  （　　 ）

A．16　　　　　 B．8　　　　　　 C．4　　　　　 D．2

21、如图，某人造卫星的远行轨道是以地球中心F₂为一个焦点的椭圆，设近地点A（离地面最近的点）距地面千米，远地点B（离地面最远的点）距地面千米，地球半径为千米，且F₂、A、B在同一直线上，则该卫星运行轨道的短半轴长为　　　　　　　  （　　 ）

A．千米　B．千米　 C．千米　 D．千米

22、已知等差数列的前项的和为S_n,若S₂₅>0，S₂₄<0，则当S_n最小时，=（　　 ）

A．11　　　　 B．12　　　　 C．13　　　　D．14

二、填空题（本题有6小题，每小题3分，共18分）

23、若，，则的最大值是　　　　  。

24、的展开式中的系数为　　　　　　  。

25、椭圆的离心率为　　　　　　　 。

26、已知，则的取值范围是　　　　　 。

27、已知二面角为，点，且点A到棱的距离为，则点A到平面的距离是　　　　　　  。

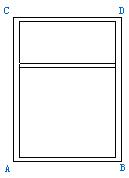
28、要制作如图所示的铝合金窗架，当窗户采光为一常数S时（中间横梁面积忽略不计），要使所用的铝合金材料最省，窗户的宽AB与高AD的比应为　　　　　　　　 。

三、解答题（本题有5小题，共38分）

29、（本题6分）已知等比数列中，a₃=18,a₄=27,求这个等比数列的通项公式。

30、（本题6分）平面内给定三个向量

（1）　　　 求；（2）若与平行，求实数。

31、（本题8分）如图，在直三棱柱ABC—A₁B₁C₁中，AB=3，BC=2，CA=。

（1）求证：BC平面ACC₁A₁；（2）当AA₁为何值时，二面角A—BC—A₁为？

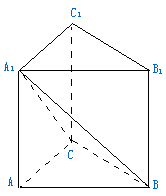
32、（本题8分）平面内一个动点P到两定点A（-，0），B（，0）的距离之和为6，设动点P的轨迹为E，

（1）求轨迹E的方程

（2）　　　 设点P（x，y）在轨迹E上，点Q（ ，0），求PQ的最小值。

33、（本题10分）第一届现代奥林匹克运动会于1896年在雅典举行，百余年后，第二十九届奥林匹克运动会将于2008年在北京举行。为表示庆贺，某数学爱好者构造了“北京奥运函数”，已知该函数满足以下条件：

①，；②在上是减函数，在上是增函数。

⑴如果某二次函数能成为“北京奥运函数”，求该函数的解析式。

⑵对于⑴中的函数，任取，证明：。

附加题（本题5分，供选做，得分计入总分）：

已知函数，当时，函数的图象恒在直线的上方，求实数的取值范围。