高二级数学知识应用竞赛试卷

从化六中高二级数学知识应用竞赛试卷

（考试时间：120分钟　　 全卷满分：100分）

题　号	一	二	三				合　计
			（9）	（10）	（11）	（12）
得　分

一、选择题：本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，只有一项是符合题目要求的．请将正确选项前的字母代号填在该小题后的括号内．

（1）某商店出售一种商品，每天能售出200件，每件能获利30元。据市场调查分析，当这种商品中的每一件每降价1元时，每天可以多售出10件，为使每天获利最多，则这种商品中的每一件应降价（　 ）

（A）3元　　 （B）5元　　（C）8元　 （D）10元

（2）我国首航员杨利伟乘坐的“神舟五号”载人宇宙飞船的运行轨道是以地球的中心F为一个焦点的椭圆，近地点A距地面为m公里，远地点B距地面为n公里．若地球的半径为R公里，则飞船运行轨道的短轴长为

(A) mn　　　　　　　　　　　　　　　　 (B) 2　

(C) 2nm　　　　　　　　　　　　　　　  (D)

（3）平面上有二个向量＝（1，0），＝（0，1），今有质点P从（-1,2）开始沿着与向量＋相同的方向作匀速直线运动，速度为＋米/秒；另一个动点Q从点（-2,-1）出发，沿着与向量3＋2相同的方向作匀速直线运动，速度为3＋2米/秒，设P、Q在时刻t＝0秒时分别在，处，则当时，t等于（　 ）

　 （A）2秒　　（B）3秒　　（Ｃ）４秒　 （D）5秒

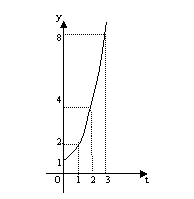（4）右图所示的某池塘中的浮萍蔓延的面积与时间（月）的关系为：.有以下判断：①这个指数函数的底数为2；②第5个月后，浮萍面积就会超过30；③浮萍从4蔓延到12只需要经过1.5个月；④浮萍每月增加的面积都相等；⑤若浮萍蔓延到,所经过的时间分别为则．其中正确判断的个数是（　）

(A) 1　　 　　　(B) 2　　　　　(C) 3　　 　　（D） 4

二、填空题：本大题共4小题，每小题5分，共20分．把答案填在题中横线上．

（5）现有一个长方体水箱，从水箱里面量得它的深是30cm，底面的长是25cm，宽是20cm．设0＜≤8，水箱里盛有深为cm的水，若往水箱里放入棱长为10cm的立方体铁块，则水深为_________cm.

（6）如图，距离船只A的正北方向100 n mile处，有一船只B

以每小时20 n mile速度，沿北偏西 角的方向行驶，船

只A以每小时15 n mile速度，向正北方向行驶，两船同时

出发，经过　　　 小时后，两船相距最近。

（7）现有一块长轴长为1米、短轴长为0.8米的椭圆形玻璃镜片，欲从此镜片中划出一块矩形镜片，则此矩形镜片的最大面积为________平方米。

（8）某工厂为某工地生产一种无盖圆柱形容器，容器的底面半径r[2，3]（米），容积为，制造容器底面的材料每平方米为30元，制造容器侧面的材料每平方米为20元，设计时材料的厚度可忽略不计，则这种容器的最低造价为　　　　　　 元．（取π＝3.14，精确到1元）

三、解答题：本大题共4小题，共60分．要求写出解答过程．

（9）（本小题满分10分）

某人身高为a,在流溪河边测得文峰塔尖的仰角为，而在流溪河的倒影中测得塔尖的俯角为，求文峰塔的高h.

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

（10）（本小题满分15分）

《中华人民共和国个人所得税法》规定，公民全月工资、奖金所得不超过800元部分不必交税，超过800元的部分为全月应纳税所得额。此项纳税按下表分段累进计算：

应纳税所得额	税率
不超过500元部分	5％
超过500元到2000元部分	10％
超过2000元到5000元部分	15％
超过5000元到20000元部分	20％
……	……

(1)有一人某月工资奖金收入额为1500元，应纳个人所得税多少元？

(2)有人某月缴纳个人所得税250元，他该月的工资奖金收入为多少？

(11) （本小题满分15分）

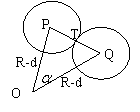
一个滚球轴承的内外圆的半径分别为R－d，R，如图所示，问：这个轴承里最多可放几个滚珠？

(12)（本小题满分20分）

　　如图，某隧道设计为双向四车道，车道总宽22米，要求通行车辆限高4.5米，隧道全长2.5千米，隧道的拱线近似地看成半个椭圆形状.

 （Ⅰ）若最大拱高h为6米，则隧道设计的拱 宽l是多少？

 （Ⅱ）若最大拱高h不小于6米，则应如何设计拱高h和拱宽l，才能使半个椭圆形隧道的土方工程量最小？（半个椭圆的面积公式为，柱体体积为：底面积乘以高.本题结果精确到0.1米，≈2.65）

从化六中高二级数学知识应用竞赛试卷答案：

（1）B（2）B（3）A （4）C

（5）（6）　（7）0.4 （8）471

（9）（本小题满分10分）

解：依题意，观测点到文峰塔的水平距离为，则

　　　　  答：（略）

（10）（本小题满分15分）

解：依题意，设某人的工资奖金收入为x元，应交纳个人所得税额为y元，则y关于x的分段函数为：

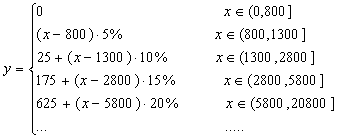
(1)当x=1500时，代入以上函数求得y=25＋（1500－1300）10％＝45(元)

(2)当y=250时，可知,代入以上函数，

250=175＋（x-2800）15%得x=3300(元)

答：（略）

(11) （本小题满分15分）

解：如图，设两圆P，Q相切于点T，连接OT

　 在Rt△OTP中

∠POT＝，OP＝R－。PT＝

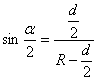则有，得

当圆心角为时，可放一个滚珠，故圆心角为周角（2π弧度）时可放的滚珠为

但滚珠数应是整数，因此放滚珠的最多数目n只能是不超过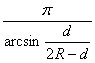的最大整数。

 (12) （本小题满分15分）

解: （Ⅰ）如图建立直角坐标系，则点P（11，4.5），　椭圆方程为.

将b=h=6与点P坐标代入椭圆方程，得.因此隧道的拱宽约为33.3米.

（Ⅱ）由椭圆方程，

得

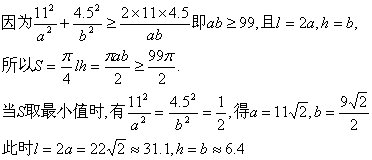
故当拱高约为6.4米、拱宽约为31.1米时，土方工程量最小。