高二空间向量及其坐标运算单元测验 2005.12.20
班级 学号 姓名
一.填空题
1、![]() =
=![]() =5,
=5, ![]() ,
,![]() 的夹角为60°,则
的夹角为60°,则![]() -
-![]() = .
= .
2、已知M=(2,-5,-3),N(-4,9,-5),则线段![]() 中点的坐标是_____________.
中点的坐标是_____________.
3.已知![]() ={3λ,6, λ+6},
={3λ,6, λ+6}, ![]() ={λ+1,3,2λ},若
={λ+1,3,2λ},若![]() ∥
∥![]() ,则λ= .
,则λ= .
4.已知![]() ={-4,3,0},则与
={-4,3,0},则与![]() 垂直的单位向量为
垂直的单位向量为![]() =
.
=
.
5. 在平行六面体![]() 中,
中,![]() 为
为![]() 与
与![]() 的交点。若
的交点。若![]() ,
,![]() ,
,![]() ,则
,则![]() =
.(用
=
.(用![]() 表示)
表示)
6. 点(x,y,z)关于z轴的对称点的坐标是 .
7. 若![]() ={3,m,4}与
={3,m,4}与![]() ={-2,2,m}的夹角为钝角,则m的取值范围是 .
={-2,2,m}的夹角为钝角,则m的取值范围是 .
8. 已知A(1,-2,-3),B(2,0,-1),![]() 的位置向量,
的位置向量, ![]() 为
为![]() 的单位向量,则单位向量
的单位向量,则单位向量![]() =
.
=
.
9.若![]() ={1,1, -4}与
={1,1, -4}与![]() ={1,-2,2},以
={1,-2,2},以![]() ,
,![]() 为邻边的平行四边形的两条对角线的长
为邻边的平行四边形的两条对角线的长
= .
10. 正四面体ABCD中,点A(0,0,0),B(4,0,0),C(2,2![]() ,0),则点D的坐标为________________.
,0),则点D的坐标为________________.
二.解答题
11. 已知![]() ,
,![]() ,
,![]() ,求满足
,求满足![]() ,
,![]() 的点
的点![]() 的坐标
的坐标
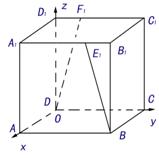
12. 正方体![]() 的棱长为2,
的棱长为2,![]() 分别为
分别为![]() 、
、![]() 的中点。
的中点。
求: ![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
|
13.如图正方体![]() 中,
中,![]() ,求
,求![]() 与
与![]() 所成角的余弦.
所成角的余弦.
高二数学单元练习测验
一.填空题
1、5 2、(-1, 2,-4) 3、2 4、{![]() } 5、
} 5、![]() 6、(-x,-y,z)
6、(-x,-y,z)
7、m<1 8、{![]() } 9、3 或3
} 9、3 或3![]() 10、(2,
10、(2,![]() )
)
二.解答题
11.( -1,1,2)
12. 证明:如图建系:![]()
则C(0,2,0)、D1(0,0,2)、M(2,0,1)、N(2,2,1)
∴![]()
∴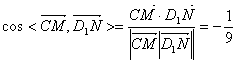
但![]() 与
与![]() 所成的角应是
所成的角应是![]() 的补角,∴
的补角,∴![]() 与
与![]() 所成的角的余弦值为
所成的角的余弦值为![]()
13. 解:不妨设正方体棱长为![]() ,建立空间直角坐标系
,建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
, ![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
 .
.
