第一学期高二数学期中试卷

河南师大附中2005年第一学期高二年级期中考试

数学试卷

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共100分，考试时间100分钟。

第Ⅰ卷（选择题　共36分）

一、选择题：本大题共12小题，每小题3分，36分.在每小题给出的4个选项中，只有一项是符合题目要求的.

1. 下列各命题中，是真命题的是

A. 如果a＞b,那么＞　　  B. 如果ac＜bc，那么a＜b

C. 如果a＞b,c＞d,那么a-c＞b-d　 D. 如果a＞b,那么a-c＞a-c

 2. 直线4x+2y+1=0的斜率是

A.-2　　　 B.2　　　　　  C.　　　　　　 D.-

 3. 设曲线F₁（x , y）=0和曲线F₂（x , y）=0的交点为P，那么曲线F₁（x , y）F₂（x , y）=0

A.必过原点　　　　　　B.必过点P　　　

C.不一定过点P　　　　 D.是否过点P无法确定

4. x²+y²≤是│x│+│y│≤1的

A.必要不必充分条件　B.充分不必要条件　　

C. 充要条件　　　　 D.既不充分又不必要条件

5. 已知实数a,b满足-1＜a＜0, b＜0,则b，ab，a²b的大小关系是

A. b＜ab＜a²b　　　　 B. b＜a²b＜ab　　

C. a²b＜b＜ab　　　　 D. ab＜a²b＜b

　　　　  x=2t-1 　　　　　　　　 x=-3+2sinθ

6. 曲线　　　　(t为参数)和曲线`　　　　　　  （θ为参数）的公共点的个数是

　　　　  y=-2t+6　　　　　　　　 y=4-2cos　

A. 一个　　 B. 两个　　　　 C. 不确定　　　　  D. 没有

　　　　　　　　　 　 x+2y-5≤0

　　　　　　　　　　  x+2y-3≥0　

7. 已知实数x,y满足　　　 ，则的最值

x≥1

　　　　　　　　　  y≥0

　A. 最大项是2，最小值是1　　　　　　 B. 最大值是1，最小值是0

C. 最大值2，最小值是0　　　　　　　 D. 无最大值是，无取小值

8. 椭圆5x²+ky²=5的一个焦点为（0，2），那么k的值是

A. -1　　　 B. 1　　　　　　  C. 　　　　 D. -

9. 椭圆+=1上一点P到左焦点的距离为，则P到右准线的距离是

　　A.　　　　　B.　　　　　　　C. 　　　 D.　

10. 下列各对方程中，表示相同曲线的一对方程是

A. y²=x与y=　　　　　　　 B. (x-1)²+(y+2)²=0与（x-1）(y+2)=0

C. y=与xy=1　　　　　　　　   D.　y=1gx²与y=21gx　

11. 已知集合M={（x,y）│x²+y²≤1，0＜y≤1},集合N={（x,y）│y=x+b,bR}，且MN=Φ，则b的取值范围是

A. b＞或b＜-1　　　　  B. -1＜b≤

C. b＞或b≤-1　　　　  D.　b≤-1

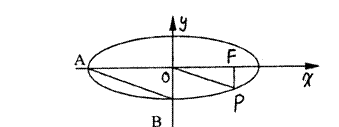12. 如图点F是椭圆的焦点，P是椭圆上一点，A、B是椭圆的顶点，且PF⊥x轴，OP∥AB，那么该椭圆的离心率是

A. 　　　B.　　　　

C.　　　　　 D.　A

二、填空题：本大题共4小题，每小题3分，共12分. 把答案填在题中横线上.

13. 点（-1，1）关于直线2x-3y=8对称的点的坐标是__________.

14. 已知点A（1，1）和B（3，3），则在x轴的正半轴上使∠AMB最大的点M的坐标是__________.

15. 不等式≤1的解集是_____________.

16. 已知实数a, b满足2b²=a²+1，则a²+4b²-4ab的最小值是__________.

三、解答题：本大题共5小题，共52分. 解答应写出文字说明、证明过程或演算步骤.

17. （本小题满分10分）

已知m, n ，a，b都是实数，且m²+n²=1,a²+b²=1, 求证│ma+nb│≤1

18 . （本小题满分10分）

如果关于x的不等式ax²+bx+c＜0的解集是{x│x＜-3或x＞2}，求关于x的不等式cx²+bx+a＞0的解集.

19.　(本小题满分10分)

一动圆M与圆A：x²+y²+6y+5=0外切，同时与圆B：x²+y²-6y-91=0内切，

（1）求圆A与B的圆心和半径，并判断两圆的位置关系：

（2）求动圆圆心M轨迹方程.

20.　(本小题满分10分)

在ΔABC中，点A（-1，5）、B（5，5）、C（6，-2）

（1）分别求AC边上的中线、BC边上的高、∠ACB的平分线所在的直线的方程；

（2）求ΔABC的外接圆的方程.

21.  ( 本小题满分12分)

经过点P（-1，2）且倾斜角为α的直线l与圆x²+y²=8的交点是A，B

（1）（理科）求弦AB的长度（用α的三角函数表示）；

　　 （文科）当α为时，求弦AB的长度；

（2）求当弦AB的长度最短时的直线l方程：

（3）（理科）过点P作垂直l的直线m，交圆于C，D两点，求弦AC的中点M的轨

迹方程

(文科)求弦AB中点M的轨迹方程

高二年级数学试卷答案.

第Ⅰ卷（选择题）答题栏

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	D	A	B	A	B	D	C	B	D	C	C	A

13.　(3,-5). 14.　(_,0)15.　{x│-2≤x (2)16.　1.

17. (本小题满分10分)

∵m²+n²=│m│²+│n│²≥│mn│

a²+b²=│a│²+│b│²≥2│ab│………………4

∴m²=n²+a²+b²≥2│mn│+2│ab│,而m²+n²=1,a²+b²=1

∴2│mn│+2│ab│≤2,即│mn│+│ab│≤1

又│ma+nb│≤│mn│+│ab│, ∴│ma+nb│≤1…………10

18. (本小题满分10分)

（1）　　　 AC边上的中线所在的直线的方程7x-5y-10=0.

BC边上的高所在的直线的方程x-7y+36=0

∠ACB的平分线所在的直线的方程2x+y-10=0 …………6

（2）∠ACB的外接圆的方程x²+y²-4x-2y-20=0…………10

19.　(本小题满分10分)

（1）圆A可化为x²+(y+3)²=4, ∴圆A的圆心（0，-3），半径2圆B可化为x²+(y-3)²=100∴圆B的圆心（0，-3），半径10

∵│AB│=6＜10-2，∴圆A与圆B内含…………5

（2）设动圆的半径为r

∵动圆M与圆A：x²+y²+6y+5=0外切，∴│MA│=2+r

∵动圆M与圆 B：x²+y²-6y-91=0内切，∴│MB│=10-r

∴│MA│+│MB│=12,既点M的轨迹是以点A、B为焦点，长轴长为12的椭圆

∴M的轨迹方程为…………10

20. （本小题满分10分）

∵不等式ax²+bx+c＜0的解集是{x│x＜-3或x＞2}

∴a＜0,且方程ax²+bx+c=0的两个根是-3、2

∵-=1，=-6　即b=a，c=-6a…………5

不等式cx²+bx+a＞0可化为-6ax²+ax+a＞0,即6x²+x+1＞0

∴x＞或x＜,∴不等式cx²+bx+a＞0的解集是{x│x＞或x＜-＝}…10

21. （本小题满分12分）　

（1）（理科）当α=90°时，│AB│=2：

当α≠90°时，│AB│=2

（文科）│AB│=………………4

（2）x-2y+5=0………………6

　　　　　　　　　　　　　　　　　　　　　  x=

　　（3）（理科）设M（x, y）,A(x₁y₁),C(x₂,y₂)则　　　　 　　　　　　　　　　　　

y=

　　　∴x₁+x₂=2x,　　　　　  y₁+y₂=2y,　　　　　　　　　　　　　　　 

x₁²+x₂²+2x₁x₂=4x² ,　　y²₁+y₂²+2y₁y₂=4y²

 x₁²+y₁²=8

 

　　　　　 又　x₂²+y₂²=8

 

∴x₁²+x₂²+y₁²+y₂²=16,　　　　　　　　  x₁x₂+y₁y₂+( x₁+x₂)-2(y₁+y₂)+5=0

∴16+2x₁x₂+y₁y₂=4x²+4y²,　　　　　　  x₁x₂+y₁y₂+2x-4y+5=0

∴2x²+2y²+2x-4y-3=0为点M的轨迹方程

（文科）∵OM⊥PM，∴弦AB中点M的轨是以OP为直径的圆

∴弦AB中点M的轨迹方程是 x+ ²+(y-1)²= …………12