博罗高级中学2005年秋季期末考试试题
高二数学(理科)
说明:本试题分选择题和非选择题两部分. 满分150分. 考试时间120分钟
.
一、选择题:(本大题共10小题,每小题5分,共50分,在每小题所给的四个选项中,只有一个是正确的。请把答案写在答题卡上。)
1.命题![]() .下列结论正确的是( )
.下列结论正确的是( )
A. ![]() 为真 B.
为真 B. ![]() 为真 C.
为真 C. ![]() 为假 D.
为假 D. ![]() 为真
为真
2.设原命题:若a+b≥2,则a,b 中至少有一个不小于1.
则原命题与其逆命题的真假情况是( )
A.原命题真,逆命题假 B.原命题假,逆命题真
C.原命题与逆命题均为真命题 D.原命题与逆命题均为假命题
3.抛物线![]() 的焦点坐标是
( )
的焦点坐标是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.
![]()
4.若f(x)=sinα-cosx,则f′(α)等于( )
A、sinα B、cosα C、sinα+cosα D、2sinα
5、方程![]() =-1表示焦点在y轴上的双曲线,则m的取值范围是
( )
=-1表示焦点在y轴上的双曲线,则m的取值范围是
( )
A.
-16<m<25 B.m<
6. 过椭圆![]() 的左焦点F引一条倾斜角为
的左焦点F引一条倾斜角为![]() 的直线,则以此直线与椭圆的两个交点及椭圆中心为顶点的三角形面积为
( )
的直线,则以此直线与椭圆的两个交点及椭圆中心为顶点的三角形面积为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.下列求导运算正确的是( )
A、![]() B、
B、![]()
C、![]() D、
D、 ![]()
8.函数![]() 有( )
有( )
A、极大值5,极小值-27 B、极大值5,极小值-11
C、极大值5,无极小值 D、极小值-27,无极大值
9. ![]() 是
是![]() 的左焦点,P为随圆上的动点A(1,1)为定点,则
的左焦点,P为随圆上的动点A(1,1)为定点,则![]() 的最小值为 (
)
的最小值为 (
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10.记定点M![]() 与抛物线
与抛物线![]() 上的点P之间距离为
上的点P之间距离为![]() ,P到抛物线准线
,P到抛物线准线![]() 的距离为
的距离为![]() ,则当
,则当![]() 取最小值时,P点坐标为 ( )
取最小值时,P点坐标为 ( )
A. (1, ![]() ) B.(0,0) C. (2 ,2 ) D.
) B.(0,0) C. (2 ,2 ) D. ![]()
二、填空题(每小题5分,共20分,请把答案写在答题卡上。)
11.椭圆与双曲线![]() 有相同的焦点F1 和F2,P为椭圆上一点,且F
有相同的焦点F1 和F2,P为椭圆上一点,且F
12、 函数![]() 的单调区间是___________________________;
的单调区间是___________________________;
13、曲线![]() 在点M(e,1)处的切线的斜率是_________,切线的方程为_______________;
在点M(e,1)处的切线的斜率是_________,切线的方程为_______________;
14、P是抛物线y2=x上的动点,Q是圆(x-3)2+y2=1的动点,则|PQ|的最小值为 .
博罗高级中学2005年秋季期末考试试题
高二数学(理科)答题卷
 一、选择题(每小题5分,共50分)
一、选择题(每小题5分,共50分)
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 |
二、填空题(每小题5分,共20分)
11. 12.
13.
14、
三、解答题(共80分)
15.(本小题10分) 已知椭圆的对称轴为坐标轴,离心率![]() ,准线方程为
,准线方程为![]() ,求椭圆的方程.
,求椭圆的方程.
16.(本小题满分14分)求函数![]() 在区间
在区间![]() 上的最大值与最小值。
上的最大值与最小值。
17.(本小题14分)命题p :关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的异根。
有两个不相等的异根。
命题q :关于![]() 的一元二次方程
的一元二次方程![]() 有两个正根。
有两个正根。
命题p和命题q有且只有一个为真,求m的取值范围。
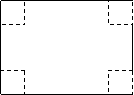
18、(本小题14分)如图,一矩形铁皮的长为
 |
19.(本小题满分14分)已知![]() 是过点
是过点![]() 的两条互相垂直的直线,且
的两条互相垂直的直线,且![]() 与双曲线
与双曲线![]() 各有两个交点,分别为
各有两个交点,分别为![]() 和
和![]() ,若
,若![]() ,求
,求![]() 的方程。
的方程。
20(本题14分)设双曲线:![]() 的焦点为F1,F2.离心率为2。
的焦点为F1,F2.离心率为2。
(1)求此双曲线渐近线L1,L2的方程;
(2)若A,B分别为L1,L2上的动点,且2![]() ,求线段AB中点M的
,求线段AB中点M的
轨迹方程,并说明轨迹是什么曲线。
博罗高级中学2005年秋季期末考试试题
高二数学(理科)参考答案
一、选择题(每小题5分,共50分)
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 | A | A | C | A | B | B | B | C | B | C |
二、填空题(每小题5分,共20分)
11.![]() 12. 增区间:
12. 增区间:![]() ,减区间:
,减区间:![]()
13. ![]() ,
,![]()
14、![]()
三、解答题(共80分)
15.(本小题10分)
解:因为椭圆的准线方程为![]() , 则设椭圆的方程为
, 则设椭圆的方程为![]()
因为![]() ,所以
,所以![]() =
=![]() ,……………………3分
,……………………3分
因为![]() , 所以
, 所以![]() ,……………………5分
,……………………5分
解得![]() ,所以
,所以![]() ……………………8分
……………………8分
所以椭圆的方程为: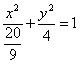 ………10分
………10分
16.(本小题满分14分)
解:![]() ,当
,当![]() 得x=0或x=-1或x=-3;………………4分
得x=0或x=-1或x=-3;………………4分
∵0![]() [-1,4],-1
[-1,4],-1![]() [-1,4],-3
[-1,4],-3![]() [-1,4],………………8分
[-1,4],………………8分
又f(0)=1,f(-1)=0;右端点处f(4)=1024+1280+320+1=2625;………………12分
∴函数![]() 在区间[-1,4]上的最大值为2625,最小值为0。…14
在区间[-1,4]上的最大值为2625,最小值为0。…14
17.(本小题14分)
解: 若命题p为真命题,则
 …………………3分
…………………3分
若命题q为真命题,则
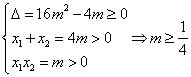 …………………7分
…………………7分
因为命题p和命题q有且只有一个为真
(1) 命题p 真, 命题q假,则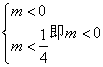 ……………10分
……………10分
(2) 命题p 假, 命题q真,则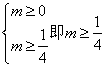 ………………12分
………………12分
由(1)(2)得m取值范围为![]() …………………14分
…………………14分
18、(本小题14分)解:设小正方形的边长为xcm,盒子容积为y=f(x);则
y=f(x)=(8-2x)(5-2x)x=4x3-26x2+40x (![]() );……………………4分
);……………………4分
∵![]() ;当
;当![]() 得
得![]() ;8分
;8分
∵![]() ,又f(1)=18,f(0)= f(
,又f(1)=18,f(0)= f(![]() )=0,
……………12分
)=0,
……………12分
∴小正方形边长为1㎝时,盒子的容积最大,为18㎝3。…………14分
19.(本小题满分14分)
解 :设![]() ,则
,则 ![]()
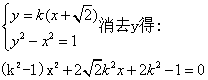 …………………4分
…………………4分
![]() …………………6分
…………………6分
![]()
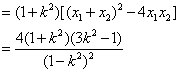
同理对于![]()
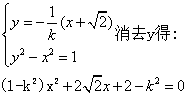
![]() …………………8分
…………………8分
由![]() 得
得
![]()
解得![]() …………………10分
…………………10分
当![]() 时,
时,
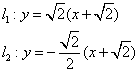 …………………12分
…………………12分
当![]() 时
时
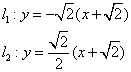 …………………14分
…………………14分
20(本题14分)设双曲线:![]() 的焦点为F1,F2.离心率为2。
的焦点为F1,F2.离心率为2。
(1)求此双曲线渐近线L1,L2的方程;(5分)
(2)若A,B分别为L1,L2上的动点,且2![]() ,求线段AB中点M的
,求线段AB中点M的
轨迹方程,并说明轨迹是什么曲线。(9分)
解:(1)由已知双曲线的离心率为2得:![]() 解得a2=1, ……………2分
解得a2=1, ……………2分
所以双曲线的方程为![]()
所以渐近线L1,L2的方程为![]() 和
和![]() =0……………5分
=0……………5分
(2)c2=a2+b2=4,得c=2 ,所以![]() ,
,
又2![]() 所以
所以![]() =10
……………3分
=10
……………3分
设A在L1上,B在L2上,设A(x1 ,![]() ,B(x2,-
,B(x2,-![]()
所以![]() 即
即![]() …………5分
…………5分
设AB的中点M的坐标为(x,y),则x=![]() ,y=
,y=![]()
所以x1+x2=2x , x1-x2=2![]() y……………7分
y……………7分
所以![]() 整理得:
整理得:![]() ……………8分
……………8分
所以线段AB中点M的轨迹方程为:![]() ,轨迹是椭圆。………9分
,轨迹是椭圆。………9分