数列的极限
【教学目标】
⒈认知目标①使学生加深对数列极限概念的理解.
②掌握数列极限的四则运算法则及运用条件.
③掌握求数列极限的一些常用方法.
⒉能力目标①培养学生观察抽象能力与严谨推理的能力.
②培养学生分析问题解决问题的能力.
⒊情感目标①激发学生勇于克服困难勤于探索的精神.
②培养学生严谨的学习态度,通过对问题转化培养辩证唯物主义观点.
【教学重点】运用数列的四则运算法则求数列的极限.
【教学难点】求含参数的式子的极限时,要注意对参数值的分类讨论.
【教学课型】复习课
【教学过程】
(一) 数列极限概念的理解.
学生课前练习:
⑴ 已知![]() ,则在区间
,则在区间![]() 外(
外(![]() 为任意小的正常数)这数列
为任意小的正常数)这数列![]() 的项数为 (填“有限项”或“无穷项”)
的项数为 (填“有限项”或“无穷项”)
⑵ 下列命题正确的是( )
①数列![]() 没有极限 ②数列
没有极限 ②数列![]() 的极限为0
③数列
的极限为0
③数列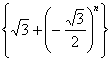 的极限为
的极限为![]() ④ 数列
④ 数列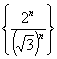 没有极限
没有极限
A ①② B ②③④ C ①②③ D ①②③④
⑶ ![]() 的( )
的( )
A 充分必要条件 B 充分不必要条件
C 必要不充分条件 D 既不充分又不必要条件
⑷ 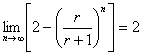 ,则r的取值范围是( )
,则r的取值范围是( )
A
-![]() B
B ![]() C
C ![]() D
D ![]()
(5) ![]() 的值为( )
的值为( )
A -![]() B -
B -![]() C
C ![]() D
D ![]()
知识归纳:
1) 数列![]() 的极限定义:
的极限定义:
任给![]() ,存在N>0,当n>N时,
,存在N>0,当n>N时,![]() 恒成立.记作
恒成立.记作![]() .
.
注意:①N与![]() 有关.②
有关.②![]() 的几何意义是当n>N时,
的几何意义是当n>N时,![]() 对应的点全部落在区间
对应的点全部落在区间![]() 之内.
之内.
2) 数列极限的运算法则:如果![]() ,
,![]() .则
.则
① ![]() .②
.② ![]() .③
.③ ![]() .
.
注意:和与积必须是有限的。
3) 几个常用极限:
① ![]() . ②
. ② ![]() . ③
. ③ ![]()
![]() .
.
4) 两种基本类型的极限:①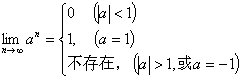
② ![]()
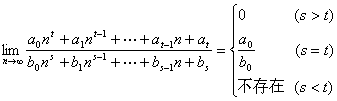
(二) 数列极限的几种求法:
例1 求下列极限
①![]()
② ![]() .
.
③ ![]() . ④
. ④ ![]()
![]() .
.
评析:1)四则运算法则只对任意有限个数列可进行四则运算,①小题数列个数是无限的,不适用于四则运算法则,因此应先求和后求极限.
2)对无穷多项的和(或积)求极限一般采用先求和(或积)后求极限.
3)分式的极限通常是分子分母同除以趋向![]() 较快的项.
较快的项.
4)求解含参数式子的极限时,应注意对参数进行分类讨论.
例2
已知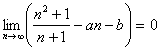 ,求实数a , b的值.
,求实数a , b的值.
评析:这是一个求待定常数的极限逆向问题,一般都是从求极限入手建立关于a, b的方程组求解
例3 数列![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列,又
的等比数列,又![]() ,
,![]() . 求
. 求![]()
评析:求一个数列前n项和的极限主要是确定和的表达式.本题解题关键是先确定![]() 为等比数列,然后求和Sn的表达式,再求极限.
为等比数列,然后求和Sn的表达式,再求极限.
(三) 归纳小结,提高认识:
⑴只有无穷数列才可能有极限,有限数列无极限.
⑵运用数列极限的运算法则求数列极限应注意法则适应的前提条件.(参与运算的数列都有极限,运算法则适应有限个数列情形)
⑶求数列极限最后往往转化为![]() 或
或![]() 型的极限.
型的极限.
⑷求极限的常用方法:
①分子、分母同时除以![]() 或
或![]() .
.
②求和(或积)的极限一般先求和(或积)再求极限.
③利用已知数列极限(如![]() 等).
等).
④含参数问题应对参数进行分类讨论求极限.
(四)目标检测,反馈调节.
① 已知等比数列![]() 的公比为q >1,则
的公比为q >1,则![]() 等于( )
等于( )
A) ![]() B)
B) ![]() C) q D) 1
C) q D) 1
② ![]() 的值为( )
的值为( )
A) ![]() B)
B) ![]() C)
C) ![]() D)
D) ![]()
③ 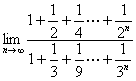 的值为
的值为
④ ![]()
⑤ 若![]() , 则
, 则![]()
⑥ 已知![]() 是以
是以![]() 为首项以
为首项以![]() 为公比的等比数列,设
为公比的等比数列,设
![]()
![]()
![]()
![]()
则A,B,C,D的大小关系
思考题:
已知数列![]() 都是由正数组成的等比数列,公比分别为p, q其中
都是由正数组成的等比数列,公比分别为p, q其中![]() ,设
,设![]() Sn为数列
Sn为数列![]() 的前n项和.求
的前n项和.求![]() .
.
(97年全国高考题)