49.共轭复数的性质、综合应用
一、典型例题
1.
已知z1=z2=z3=r≠0,求复数 的模。
的模。
2.
若z1,z2∈C,求证:z1![]() =1-z1z2成立的充分必要条件是z1、z2中至少有一个是1。
=1-z1z2成立的充分必要条件是z1、z2中至少有一个是1。
3.
设z是虚数,求证:![]() 为纯虚数的充要条件是z=1。
为纯虚数的充要条件是z=1。
4.
设复数z1和z2满足z1·![]() +
+![]() ·z1+A·
·z1+A·![]() =0,其中A=
=0,其中A=![]() ,求z1+A·z2+A的值。
,求z1+A·z2+A的值。
5.
已知z1、z2∈C且A=z1·![]() +
+![]() ·z2,B=z1·
·z2,B=z1·![]() +z2·
+z2·![]() ,问A与B是否可以比较大小?若能,哪个较大?
,问A与B是否可以比较大小?若能,哪个较大?
6.
已知a、b、c∈R,求证:![]() 。
。
7.
已知a、b、c∈R+,求![]() 的最小值。
的最小值。
8.
求值:① ![]() ;②
;②![]() 。
。
9. n为何值时,x2n+1+(x+1)2n (n∈Z)能被x2+x+1整除?
10.
求S=![]() 的值。
的值。
11.
求和:![]() (n∈N)。
(n∈N)。
12.
 证明:arctg
证明:arctg![]() + arctg
+ arctg![]() + arctg
+ arctg![]() + arctg
+ arctg![]() =
=![]() 。
。
13. 求以A(1,0)、B(2,1)为两顶点的正三角形ABC顶点C的坐标。
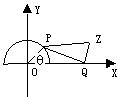
14. 如图:P为半圆x2+y2=1(x≤1,y≥0)上一动点,Q(2,0)是x轴上一定点,⊿PQZ是以PZ为斜边的等腰直角三角形,问P点位于何处时,O、Z两点间的距离最大?并求此最大值。
15. 已知椭圆5x2+9y2=45的右焦点为F,Q是椭圆上任意一点,且⊿FPQ是等边三角形(F、
P、Q成逆时针方向排列),当点Q在这个椭圆上运动时,求点P的轨迹方程。
16.
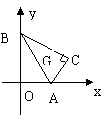 如图:设长度为2的线段AB的两个端点A、B分别在x轴正半轴上和y轴正半轴上滑动,以AB为斜边作等直角⊿ABC,并使直角顶点C恒在第一象限内,试求⊿ABC的重心G的轨迹。
如图:设长度为2的线段AB的两个端点A、B分别在x轴正半轴上和y轴正半轴上滑动,以AB为斜边作等直角⊿ABC,并使直角顶点C恒在第一象限内,试求⊿ABC的重心G的轨迹。