参数方程极座标复习题85

85．圆锥曲线的参数方程

一、典型例题

1．  A为椭圆上任一点，B为圆(x-1)²+y²=1上任一点，求AB 的最大值和最小值。

2．  在圆x²+y²=4上有一定点A(2,0)和两个动点B，C，且∠BAC=，求⊿ABC的重心G的轨迹。

3．  如果椭圆的右焦点和右项点分别是双曲线 (q为参数)的左焦点和左顶点，且椭圆焦点到相应准线的距离为，求这椭圆上的点到双曲线渐近线的最短距离。

4．  求

5．  曲线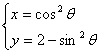 （q为参数）与（t为参数）公共点的个数。

6．  直线l:ax+by+c=0与曲线y=交于A，B两点，设OA，OB的倾斜角分别为a,b，求sin(a+b)的值。

7．  设椭圆的中心是坐标原点，长轴在x轴上，离心率e=，已知点P(0,)到这个椭圆上的点的最远距离为，求这个椭圆方程。

8．