2004-2005学年度上学期
高中学生学科素质训练
高二数学同步测试(4)—不等式综合
一、选择题(本大题共10小题,每小题5分,共50分)
1.若a<b<0,则
( )A. ![]() B. 0<
B. 0<![]() <1 C. ab>b2 D.
<1 C. ab>b2 D. ![]()
2.若a+c<b,则 ( )A. a<b-c B. a>c-b C. a>b-c D. a<c-b
3.设a=![]() ,则a,b,c的大小顺序是
( )
,则a,b,c的大小顺序是
( )
A. a>b>c B. a>c>b C. c>a>b D. b>c>a
4. 设b<0<a,d<c<0,则下列各不等式中必成立的是 ( )A. ac>bd B. ![]() C. a+c>b+d D. a-c>b-d
C. a+c>b+d D. a-c>b-d
5.下列命题中正确的一个是 ( )
A.![]() ≥2成立当且仅当a,b均为正数
≥2成立当且仅当a,b均为正数
B.![]() 成立当且仅当a,b均为正数
成立当且仅当a,b均为正数
C.logab+logab≥2成立当且仅当a,b∈(1,+∞)
D.a+![]() ≥2成立当且仅当a≠0
≥2成立当且仅当a≠0
6.函数y=log![]() 的定义域是
( )
的定义域是
( )
A.x≤1或x≥3 B.x<-2或x>1 C.x<-2或x≥3 D.x<-2或x>3
7.已知x,y∈R,命题甲: x-1<5,命题乙: x-1<5,那么 ( )
A.甲是乙的充分条件,但不是乙的必要条件
B.甲是乙的必要条件,但不是乙的充要条件
C.甲是乙的充要条件
D.甲不是乙的充分条件,也不是乙的必要条件
8.已知实数x,y满足x2+y2=1,则代数式(1-xy)(1+xy)有 ( )
A.最小值![]() 和最大值1 B.最小值
和最大值1 B.最小值![]() 和最大值1
和最大值1
C.最小值![]() 和最大值
和最大值![]() D.最小值1
D.最小值1
9.关于x的方程ax2+2x-1=0至少有一个正的实根的充要条件是 ( )
A.a≥0 B.-1≤a<0
C.a>0或-1<a<0 D.a≥-1
10.函数y=![]() (x>0)的最小值是
( )
(x>0)的最小值是
( )
A.2![]() B.-1+2
B.-1+2![]() C.1+2
C.1+2![]() D.-2+2
D.-2+2![]()
二、填空题(本大题共4小题,每小题6分,共24分)
11.关于x的不等式a
x 2+b x +2>0的解集是![]() ,则a +b=_____________.
,则a +b=_____________.
12.实数![]() _________,y=_________.
_________,y=_________.
13.方程![]() 又一正根一负根,则实数
又一正根一负根,则实数![]() 的取值范围是
.
的取值范围是
.
14.建造一个容积8![]() ,深为
,深为![]() 长的游泳池,若池底和池壁的造价每平方米分别为120元和80元,则游泳池的最低总造价为__________元.
长的游泳池,若池底和池壁的造价每平方米分别为120元和80元,则游泳池的最低总造价为__________元.
三、解答题(本大题共6题,共76分)
15.已知![]() (12分)
(12分)
16.解关于x的不等式![]() .(12分)
.(12分)
17.已知: x > y >0 , 且xy=1, 若![]() 恒成立,求实数a的取值范围.(12分)
恒成立,求实数a的取值范围.(12分)
18.解关于![]() .(12分)
.(12分)
19.设f(x)是定义在![]() 的奇函数,g(x)的图象与f(x)的图象关于直线x=1对称,而当
的奇函数,g(x)的图象与f(x)的图象关于直线x=1对称,而当![]() 时,
时,![]() .
.
(1)求f(x)的解析式;
(2)对于任意的![]() 求证:
求证:![]()
(3)对于任意的![]() 求证:
求证:![]() (14分)
(14分)
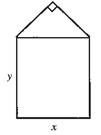 20.某单位用木料制作如图所示的框架, 框架的下部是边长分别为x、y(单位:m)的矩形.上部是等腰直角三角形. 要求框架围成的总面积8cm2. 问x、y分别为多少(精确到0.001m)
时用料最省?(14分)
20.某单位用木料制作如图所示的框架, 框架的下部是边长分别为x、y(单位:m)的矩形.上部是等腰直角三角形. 要求框架围成的总面积8cm2. 问x、y分别为多少(精确到0.001m)
时用料最省?(14分)
参考答案
一、选择题(本大题共10小题,每小题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | B | B | C | D | D | A | B | D | B |
二、填空题(本大题共4小题,每小题6分,共24分)
11.-14 12.1,2,1 13.![]() 14. 1760
14. 1760
三、解答题(本大题共6题,共76分)
15.(12分)
[解析]: 左边=![]() ,
,
![]() .
.
16.(12分)
[解析]:原不等式
![]()

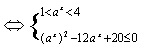
![]() ,
,
∴当a>1时,原不等式的解集为:![]() ;
;
当0<a<1时,原不等式的解集为:![]() .
.
17.(12分)
[解析]: ![]() ,
,![]()
原题意![]()
![]() .
.
18.(12分)
[解析]:![]() 原不等式
原不等式![]() .
.
①当![]()
![]() ;
;
②当![]()
![]() ;
;
③当![]()
![]()
19.(14分)
[解析]:(1)由题意知f(x+1)=g(1-x)![]()
当![]()
当![]() ,由于f(x)是奇函数
,由于f(x)是奇函数![]()
![]()
(2)当![]()
![]()
(3)当![]()
![]()
![]()
20.(14分)
[解析]:由题意得 xy+![]() x2=8,∴y=
x2=8,∴y=![]() =
=![]() (0<x<4
(0<x<4![]() ).
).
于定, 框架用料长度为 l=2x+2y+2(![]() )=(
)=(![]() +
+![]() )x+
)x+![]() ≥4
≥4![]() .
.
当(![]() +
+![]() )x=
)x=![]() ,即x=8-4
,即x=8-4![]() 时等号成立.
时等号成立.
此时, x≈2.343, y=2![]() ≈2.828.
≈2.828.
故当x为2.343m, y为2.828m时, 用料最省.