北京市宣武区2001—2002学年度第二学期第二次质量检测
高三文科数学试题
第一卷(选择题共60分)
参考公式
三角函数的和差化积公式 圆台的体积公式
![]()
![]()
![]() 其中r1,r2分别为圆的上、下底面半径,
其中r1,r2分别为圆的上、下底面半径,
![]() h表示圆台的高
h表示圆台的高
![]() 球体的体积公式
球体的体积公式 ![]()
其中R表示球的半径
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)设集合![]() 则实数m的取值范围是
则实数m的取值范围是
A.m ≥ -1 B.m > –1 C.m ≤ -1 D.m < -1
(2)若直线l过点(3,0)且与双曲线![]() 只有一个公共点,则这样的直线有
只有一个公共点,则这样的直线有
A.1条 B.2条 C.3条 D.4条
(3)z+4+3i 3中的复数据z的模应满足的不等式是
A.z < 8 B.z ≤ -4-3i C.2≤z≤8 D.5≤z≤8
(4)在复平面内,把复数![]() 对应的向量按顺时针方向旋转
对应的向量按顺时针方向旋转![]() ,所得向量对应的复数是
,所得向量对应的复数是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(5)设P(x,y)是曲线C:![]() 上任意一点,则
上任意一点,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(6)A、B、C、D、E五种不同的商品要在货架上排成一排,其中A、B两种商品必须排在一起,而C、D两种商品不能排在一起,则不同的排法共有
A.12种 B.20种 C.24种 D.48种
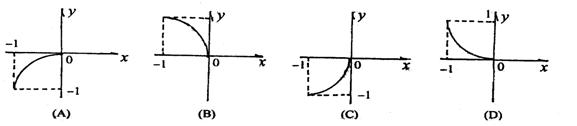
(7)设函数![]() 的图像是
的图像是
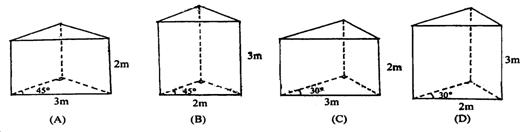
 (8)用一块长3m,宽2m的矩形木板,在二面角为90O的墙角处,围出一个直三棱柱形谷仓,在下面的四种设计中,容积最大的是
(8)用一块长3m,宽2m的矩形木板,在二面角为90O的墙角处,围出一个直三棱柱形谷仓,在下面的四种设计中,容积最大的是
(9)在等比数列{an}中,![]() 等于
等于
A.6 B.-6 C.±2 D.±6
(10)已知凸函数,则对于区间D内的任意![]()
若函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(11)一个半径为R的球,在一个水平放置的,内壁为半圆信形(圆柱底面半径也是R)的槽内恰好可以无滑动地滚动一周,从槽的一端滚向另一端,设球的表面积为s,槽的内壁面积为s′,则s与s′的大小关系是
A.s =s′ B.s <s′ C.s >s′ D.不确定
(12)若![]() 的大小关系是
的大小关系是
A.![]() B.
B.![]()
C.![]() D.不确定
D.不确定
第二卷(非选择题共90分)
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上
(13)若![]() 展开式中各项系数的和为128,则展开式中x2项的系数为__________________________________。
展开式中各项系数的和为128,则展开式中x2项的系数为__________________________________。
(14)是正实数,如果函数![]() 上是增函数,那么的取值范围是——。
上是增函数,那么的取值范围是——。
(15)在数列{an}中,an>0,sn是它的前n项和,且![]() ,则它的通项公式是an =______________________。
,则它的通项公式是an =______________________。
(16)已知椭圆![]() ,是它的两个焦点,若P是椭圆上任意一点,
,是它的两个焦点,若P是椭圆上任意一点,![]() 的最小值是___________________________________。
的最小值是___________________________________。
三、解答题:本大题共6小题共74分,解答应写出文字说明,证明过程或演算步骤
(17)(本题满分12分)
在△ABC中,角A、B、C所对的边分别为a,b,c若a,b,c成等比数列。
(Ⅰ)求证:![]() ;
;
(Ⅱ)求![]() 的取值范围。
的取值范围。
(18)(本题满分12分)
已知![]()
(Ⅰ)求函数![]() ;
;
(Ⅱ)试比较![]() 的大小。
的大小。
(19))(本小题满分12分)
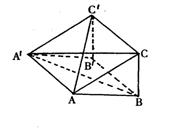
如图,在三棱柱ABC—A′B′C′中,四边形A′ABB′是菱形,四边形BCC′B′是矩形,C′B′⊥AB。
(Ⅰ)求证:平面CA′B⊥平面A′AB;
(Ⅱ)若C′B′=3,AB=4,∠ABB′=60O,求直线AC′与平面BCC′所成角的正弦值。
(20)(本小题满分12分)
有甲、乙两种商品,经营销售这两种商品所能获得的利润依次为P万元和Q万元,它们与投入资金x(万元)的关系有经验公式![]() 。现有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别是多少?
。现有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别是多少?
(21)(本小题满分13分)
已知椭圆中心在原占,以抛物线![]() 的焦点为其右焦点,并且椭圆的长轴长、短轴长、焦距成等差数列,A、B是椭圆上两点,弦AB中点M在直线x=4上。
的焦点为其右焦点,并且椭圆的长轴长、短轴长、焦距成等差数列,A、B是椭圆上两点,弦AB中点M在直线x=4上。
(Ⅰ)求椭圆方程;
(Ⅱ)求证弦AB的垂直平分线l与x轴交于定点。
(22)(本小题满分13分)
已知函数![]() ,记数列{ an }的前n项和为s n,且有
,记数列{ an }的前n项和为s n,且有![]() 当n≥2时,
当n≥2时,
![]() 。
。
(Ⅰ)计算a 1;a 2 ;a 3 ;a 4 。
(Ⅱ)求出数列{ an }的通项公式,并给予证明。