北京市西城区抽样测试高三数学(文科)答案及评分标准
2001.6
一、CCDCB DDABA AB.
二、(13)![]() (14)
(14)![]() ;(15)36cm;(16)①③
;(15)36cm;(16)①③![]() ②④;②③
②④;②③![]() ①④.
①④.
三、解答题:其它解法仿此给分.
(17)解:原不等式等价于
设![]() 则t>0且
则t>0且

∴![]()
即![]()
∴![]() .………………………………………11分
.………………………………………11分
∴原不等式的解集为![]() .……………12分
.……………12分
(18)解:(1)证明∵a+c=2b ∴![]() .………………1分
.………………1分
∴![]() .…4分
.…4分
∵![]() .
.
∴![]() .…………………………………………6分
.…………………………………………6分
(2)解:![]()
![]()
![]() …………………………………………9分
…………………………………………9分
![]()
![]() ………11分
………11分
![]()
=1.…………………………………………………………………12分
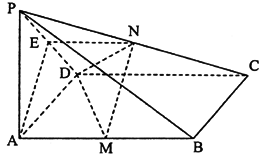
(19)解:(1)PA⊥平面ABCD,CD⊥AD,∴PD⊥CD.
故∠PDA是平面PCD与平面ABCD所成二面角的平面角.…2分
在Rt△PAD中,PA⊥AD,PA=AD,∴∠PDA=45°.………3分
(2)取PD中点E,连结AE,EN,又M,N分别是AB,PC的中点,
∴![]()
![]()
![]()
![]()
![]() ∴AMNE是平行四边形,
∴AMNE是平行四边形,
∴MN∥AE.…………………………………………………………5分
在等腰Rt△PAD中,AE是斜边的中线,
∴AE⊥PD.
又CD⊥AD,CD⊥PD ∴CD⊥平面PAD
∴CD⊥AE,………………………………………………………7分
又PD∩CD=D,∴AE⊥平面PCD.
∴MN⊥平面PCD.…………………………………………………8分
(3)∵AD∥BC,
所以∠PCB为异面直线PC,AD所成的角.………………………9分
由三垂线定理知PB⊥BC,设AB=x(x>0).
∴![]() .…………………………10分
.…………………………10分
![]() ∴
∴![]() ………………………………11分
………………………………11分
又∠PCB为锐角,∴![]() .
.
即异面直线PC,AD所成的角的范围为![]() .……………12分
.……………12分
(20)解:(1)椭圆![]() 的两个焦点坐标是
的两个焦点坐标是![]() .离心率
.离心率![]() .……3分
.……3分
由![]() 可知双曲线
可知双曲线![]() 的离心率
的离心率![]() .……………………4分
.……………………4分
∴![]() .………………………………5分
.………………………………5分
故双曲线![]() 的方程为
的方程为![]() .……………………6分
.……………………6分
(2)∵圆D经过双曲线的两个焦点,∴圆心D在直线x= –2上.……7分
设圆D的方程为![]() .………………8分
.………………8分
整理得:![]() .
.
令y=0,得![]() .……………………………………9分
.……………………………………9分
设圆D与x轴的两个交点为(![]() ),(
),(![]() ),则
),则
![]() ..
..
依题意![]() =
=![]() .
.
即16–4(2b–22)=64,解得b=5.……………………………………12分
所以圆的方程为![]() .……………………………13分
.……………………………13分
(21)解:依题意,价格上涨x%后,销售总金额为:
![]() ……………………………………………2分
……………………………………………2分
![]() .………………………………4分
.………………………………4分
(1)取![]()
![]() .
.
∴x=50即商品价格上涨50%时,y最大为![]() .……………………7分
.……………………7分
(2)因为![]() .
.
此二次函数开口向下,对称轴为![]() ,……………………………9分
,……………………………9分
在适当涨价过程中,销售总金额不断增加,即要求此函数当自变量x在{xx>0}的一个子集内增大时,y也增大。
所在![]() ,解之0<k<1……………………………………………………12分
,解之0<k<1……………………………………………………12分
(22)解:依题意![]() ……①
……①
![]() ……②……………………………………………………2分
……②……………………………………………………2分
(I)∵![]() ,∴由②式得
,∴由②式得![]() .
.
从而![]() 时,
时,![]() .
.
代入①![]() ,∴
,∴![]() ………………5分
………………5分
∴![]() 是等差数列。………………………………………………………
6分
是等差数列。………………………………………………………
6分
(II)由![]() 及①②两式易得
及①②两式易得![]()
∴![]() 中公差
中公差![]() .
.
∴![]() .……………………………………10分
.……………………………………10分
∴![]() ………………③
………………③
又![]() 也适合③ ∴
也适合③ ∴![]() ……………11分
……………11分
∴![]() .
.
∴![]() .
.
∴![]() .………………………………………………………………13分
.………………………………………………………………13分