1．在首项为81，公差为－7的等差数列
中，最接近零的是第
项
2．等差数列{an}的前n项和为Sn，若a4=18－a5，则S8等于：
|
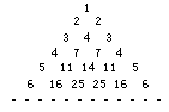
3．如下表，它满足（1）第n行首尾两数均为n，（2）表中的递推
关系，类似杨辉三角，则第n行（n≥2）第2个数是 ．
4． 有200根相同的钢管，把它们堆放成正三角形垛，要使剩余的钢管尽可能少，那么剩余钢管的根数为： A．9 B．10 C．19 D．29
5．等差数列
中，
＝－5，它的前11项的平均值是5，若从中抽取1项，余下10项的平均值是4，则抽取的是：
A．
B．
C．
D．
6．将正偶数按下表排成4列：第1列 第2列 第3列 第4列
第1行 2 4 6 8
第2行 16 14 12 10
第3行 18 20 22 24
…… 28 26
则2000在： A．第125行，第1列 B．第125行，第2列
C．第250行，第1列 D．第250行，第4列
7．随着科技发展计算机价格不断降低，每年计算机价格降低
，2000年价格为8100元的计算机，2004年价格可降为：
A．1800 B．1600 C．900 D．300
8．1980年我国工农业总产值为a千亿元，要实现邓小平同志提出的到2000年工农业总产值翻两翻的战略目标，年平均增长率至少应达到： (A) 
(B) 
(C) 
(D) 
9．制造某机器配件的一道工序是：用汽锤把厚度为a 厘米的金属工件锻造成厚度不多于原厚度的83％的工件．现知汽锤每冲击一次后，工件的厚度就比这次冲击前的厚度降低3％，则至少需冲击 次．
10．在等比数列
中，首项
，则是递增数列的充要条件是公比q满足：
A．q>1 B．q<1 C．0<q<1 D．q<0
11．等比数列的前n项和
，则k的值是：A．全体实数 B．－1 C．1 D．3
12．在3与24之间插入5个实数，使这7个数成等比数列，这个数列的第4项是
13．二进制数即“逢2进1”，如（1101）2，表示二进制数，将它转换成十进制形式是
，那么二进制数
，转换成十进制形式是：
（A）22002－１ （B）22001－2 （C）22001－１ （D）22000－１
14．已知数列
的通项公式为
则关于an的最大、最小项叙述正确的是：
（A）最大项为a1，最小项a3（B）最大项为a1，最小项不存在
（C）最大项不存在，最小项为a3（D）最大项a1，最小项a4
15．数列1，1+2，1+2+22，……，1+2+22+……+2n-1，……的前n项和是Sn=
16．无穷等比数列的第一项等于第二项开始隔一项的以后各项的和的3倍,则这个数列的公比为
17．
.
18．
等于：（A）16 （B）8 （C）4 （D）2
19． 已知各项均为正数的等比数列{an}的首项a1=1,公比为q,前n项和为Sn,
=1,则公比q的取值范围是： A.q≥1 B.0<q≤1 C.0<q<1 D.q>1
20．用数学归纳法证明：x2n-y2n (n∈Z+)能被x+y 整除的第二步是：假设n=k(k∈Z+)时，x2k-y2k 能被x+y 整除，证当n=k+1时，x2（k+1）-y2（k+1）也能被x+y 整除。则在证明过程中，x2（k+1）-y2（k+1） 的合理变形是： (A)( xk+1+yk+1)(xk+1-yk+1) (B) x2k(x2 +y2)-y2 (x2k+y2k) (C) x2(x2k-y2k)+y2k (x2 -y2) (D) x2(x2k+y2k)-y2k (x2 +y2)
21．设数列{a n}的前n项和为S n，已知an=5S n－3 (n∈N)，求a 1+a 3+…+a 2 n－1的值．
22．数列是等比数列，
＝8，设
，如果数列
的前7项和
是它的前n项和组成的数列
的最大值，且
，求
的公比q的取值范围．
23．已知数列{an}的通项公式an=9-2n，则Hn= a1+ a2+…+ an= ．
24．已知数列{an}的前n项和
（1）求数列{an}和{bn}的通项；（2）求证存在自然数n0,对一切不小n0的自然数n，恒有an>5bn.
25．（1）解不等式
；（2）设f(k)是满足上述不等式的正整数x的个数，求f(k)的解析式；（3）记
的表达式；（4）令
试比较Sn与
的大小.
26．某房屋开发商出售一套50万元的住宅，可以首付5万元，以后每一年付5万元，直到付清，也可以一次付清，并优惠x%，问开发商怎样确定优惠率可以鼓励购房者一次付款。（年复利率2%，x取整数）
27．某地今年年初有居民住房面积为a m2,其中需要拆除的旧房面积占了一半．当地有关部门决定每年以当年年初住房面积的10%的住房增长率建设新住房，同时每年拆除x m2的旧住房，又知该地区人口年增长率为4.9‰．（1）如果10年后该地的人均住房面积正好比目前翻一番，那么每年应拆除的旧住房面积x是多少？ （2）依照(1)拆房速度，共需多少年能拆除所有需要拆除的旧住房？
28．有一条生产流水线，由于改进了设备，预计第一年产量的增长率为150%，以后每年的增长率是前一年的一半，设原来的产量为a. （Ⅰ）写出改进设备后的第一年，第二年，第三年的产量，并写出第n与第n―1年n≥2，n∈N）的产量之间的关系式； （Ⅱ）由于设备不断老化，估计每年将损失年产量的10%，请说明从第几年起，产量将比上一年减少.
29．已知函数f(x)=loga (a>0且a≠1). (1)设点A是函数f(x)的图象上的点，点B与点A关于点(，1)对称，则点B是否在函数f(x)的图象上？并说明理由； (2)设f(x)的反函数是g(x)，若g(x1) +g(x2)=1，比较x12+x22与x1+x2的大小； (3)令bn= (n∈N)，如果对一切自然数n，不等式bn+1>n2恒成立，试找出自然数a的最小值，并证明你的结论。