顺义三中高2006级高一上学期数学试题六
1.设全集![]() ,集合
,集合![]() ,
,![]() ,则
,则![]() 是
是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设![]() 为给定的实数,则集合
为给定的实数,则集合![]() 的子集的个数是
的子集的个数是
![]()
![]()
![]()
![]()
![]()
![]()
![]() 不确定
不确定
3.已知集合![]() ,由集合
,由集合![]() 的所有元素组成集合
的所有元素组成集合![]() ,则这样的实数
,则这样的实数![]() 共有A.1个 B.2个 C.3个 D.4个
共有A.1个 B.2个 C.3个 D.4个
4.已知以下四个命题:① 如果![]() 是一元二次方程
是一元二次方程![]() 的两个实根,且
的两个实根,且![]() ,那么不等式
,那么不等式![]() 的解集为
的解集为![]() ;②若
;②若![]() ,则
,则![]() ;
;
③“若![]() ,则
,则![]() 的解集是实数集
的解集是实数集![]() ”的逆否命题;
”的逆否命题;
④ “若![]() ,
,![]() ,则
,则![]() ”的逆否命题。其中为真命题的是
”的逆否命题。其中为真命题的是
A.①、③ B.②、④ C.①、④ D.①、②
5.已知映射![]() :
:![]() ,其中集合
,其中集合![]() (
(![]() 是自然数集),且对任意的
是自然数集),且对任意的![]() ,在
,在![]() 中和它对应的元素是
中和它对应的元素是![]() ,则集合
,则集合![]() 中元素
中元素![]() 的原象是A.0 B.1 C.2 D.3
的原象是A.0 B.1 C.2 D.3
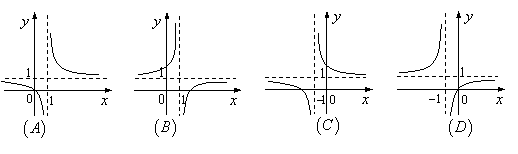 6. 函数
6. 函数 ![]() 的图象是
的图象是
7.若不等式![]() 对于
对于![]() 恒成立,那么实数
恒成立,那么实数![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知集合![]() ,则
,则![]() 的关系是
的关系是
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
9.若不等式ax2 +bx+c>0的解是0<α<x<β,则不等式cx2- bx +a>0的解为
A.![]() <x<
<x<![]() B.-
B.-![]() <x<—
<x<— ![]() C.-
C.-![]() <x<-
<x<-![]() D.
D. ![]() < x<
< x<![]()
10. 函数![]() 是单调函数的充要条件是A.b≥0 B.b≤0
是单调函数的充要条件是A.b≥0 B.b≤0
C.b>0 D.b<0
11.设函数![]() 满足条件:①
满足条件:①![]()
![]() ;②当
;②当![]() 时,
时,![]() 为增函数,则
为增函数,则![]() ,
,![]() ,
,![]() 的大小顺序是
的大小顺序是![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
12. 已知函数![]() 是定义域为
是定义域为![]() 的偶函数,在
的偶函数,在![]() 上是增函数,且
上是增函数,且![]() ,则不等式
,则不等式![]() 的解集为A.
的解集为A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13. 已知函数![]() 的定义域为
的定义域为![]() ,则
,则![]() 的定义域为_______________;
的定义域为_______________;
14.若非空集S![]() {1,2,3,4,5},且若a∈S,必有(6-a)∈S,则所有满足上述条件的集合S共有
个。
{1,2,3,4,5},且若a∈S,必有(6-a)∈S,则所有满足上述条件的集合S共有
个。
15.函数![]() 的单调递增区间是____ ___________;
的单调递增区间是____ ___________;
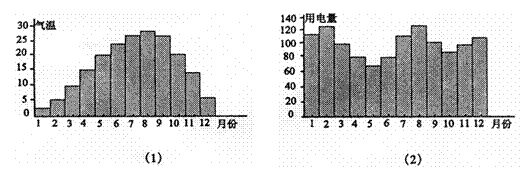
16.一般地,家庭用电量![]() (千瓦)与气温
(千瓦)与气温![]() (℃)有函数关系
(℃)有函数关系![]() 。图(1)表示某年12个月中每月的平均气温,图(2)表示某家庭在12个月中每月的用电量。试在数集
。图(1)表示某年12个月中每月的平均气温,图(2)表示某家庭在12个月中每月的用电量。试在数集![]() 是2.5的整数倍}中确定一个最小值
是2.5的整数倍}中确定一个最小值![]() 和最大值
和最大值![]() ,使
,使![]() 上的增函数,则区间[
上的增函数,则区间[![]() ,x2]=
。
,x2]=
。
 |
17.(本小题12分)已知全集U=R,集合A={x![]()
![]() 3},B={x-
3},B={x-![]() },
},
求CU(A ![]() B)。
B)。
18.(本小题![]() 分)判断下列函数的奇偶性:⑴
分)判断下列函数的奇偶性:⑴![]() ;
;
⑵![]()
![]() ;⑶
;⑶![]()
![]() ; ⑷
; ⑷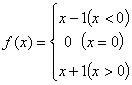 。
。
19.(本题满分![]() 分)用反证法证明:直角三角形斜边上的中点到三顶点的距离相等.
分)用反证法证明:直角三角形斜边上的中点到三顶点的距离相等.
20.(本题满分![]() 分)利用定义讨论函数
分)利用定义讨论函数![]()
![]() 在
在![]() 上的单调性.
上的单调性.
21.(本题满分14分)某校校长暑假将带领该校市级“三好生”去北京旅游。甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优待。”乙旅行社说:“包括校长在内,全部按全票价的6折(即
按全票价的60%收费)优惠。”设全票价为240元。
(I)设学生数为x,甲旅行社收费为![]() ,乙旅行社收费为
,乙旅行社收费为![]() ,分别计算两家旅行社的收费(建立表达式);
,分别计算两家旅行社的收费(建立表达式);
(II)当学生数是多少时,两家旅行社的收费一样;
(III)就学生数x讨论哪家旅行社更优惠.
22.(本题满分14分)已知![]() ≤
≤![]() ≤1,若函数
≤1,若函数![]() 在区间[1,3]上的最大值为
在区间[1,3]上的最大值为![]() ,最小值为
,最小值为![]() ,令
,令![]() .
.
(1)求![]() 的函数表达式;
的函数表达式;
(2)判断函数![]() 在区间[
在区间[![]() ,1]上的单调性,并求出
,1]上的单调性,并求出![]() 的最小值 .
的最小值 .
23、(本小题为附加题,如果解答正确,加![]() 分,但全卷总分不超过150分)
分,但全卷总分不超过150分)
若不等式2x-1> m(x2-1)对满足-2 ≤ x ≤2 的所有实数m都成立,求实数x的取值范围是。
欢迎访问 http://www.k12zy.com