数学能力专题训练（数形结合）
要点：
数形结合：就是通过数与形之间的对应和转化来解决数学问题，它包含以形助数和以数解形两个方面。利用它可使复杂问题简单化、抽象问题具体化，它兼有数的严谨与形的直观之长，是优化解题过程的重要途径之一，是一种基本的数学方法。
一，选择题 。
1，已知I={1，2，3，4，5，6，7，8，9，10}为全集，集合A、B为全集I的子集，且
A
={1，4，7}，
B={2，3}，={6，8，9，10}，那么集合A等于( )
A、{1，4，5，6，7，8，9，10} B、{1，4，7}
C、{1，4，5，7} D、{1，2，3，4，5，7}
2, 函数y=log2x－1的单调递减区间是 （ ）
A、(－¥，－2)与(－1，0] B、[－2，－1)与[0，＋¥)
C、(－¥，0]与(1，2]
D、[0，1)与[2，＋¥)
3，若奇函数y=f(x)(x¹0)，在xÎ(0，＋¥)时，f(x)=x－1，那么f(x－1)<0的x的集合（ ）
A、{x1<x<2} B、{x－1<x<0} C、{xx<0或1<x<2} D、{xx<－2或－1<x<0}
4，设复数z满足arg(x＋i)=
，则
的最大值是
（ ）
A、
B、
C、
D、
5，若曲线y=
(0£x£2)与直线y=k(x－2)＋2有两个交点，则实数k的取值范围为
(
)
A、(
，1) B、(，＋¥)
C、(，1] D、[，＋¥)
6，函数f(x)=Msin(wx+j)(w>0)在区间[a，b]上是增函数，且f(a)=－M，f(b)=M，则函数g(x)=Mcos(wx+j)在[a，b]上 （ ）
A、是增函数
B、是减函数
C、可以取得最大值M D、可以取得最小值－M
7，复数z满足z£
，则1－z的辐角主值的取值范围是
(
)
A、[0，
]
[
，2p) B、[
，
] C、[0，][，2
) D、[－，]
8，已知函数y=loga(－x2＋log2ax)对任意xÎ(0，)有意义，则实数a的取值范围为( )
A、0<a< B、
<a< C、<a<1
D、a>1
9, 已知f(x)=2－x2，g(x)=x，规定：当f(x)£g(x)时f(x)g(x)=f(x)，当f(x)>g(x)时f(x)g(x)=g(x)，则f(x)g(x)的最大值为 ( )
A、2
B、1
C、
D、不能确定
10，当xÎ[0，
]时，不等式sinx>>cosx的解集是
( )
A、(，)
B、(，)
C、(，] D、F
11，若已知集合A={xlg(x2－2ax＋a2＋1)<lg2}，B={x(x－a)(x－2)>0}，若AB=R，则实数a的取值范围为
(
)
A、(1，4) B、(1，3) C、[1，3] D、[1，3)
12，已知an=
(nÎN)，则数列{an}的前20项中最大项和最小项分别为 ( )
A、a1，a20 B、a9，a10 C、a1，a9 D、a10，a20
二，填空题。
13，若实数x，y满足：(x－2)2＋y2=3，则
的取值范围为_______________________。
14，已知函数f(x)=x2＋ax＋3，当xÎ[－2，2]时，f(x)³a恒成立，则实数a的取值范围为________________________。
15，已知方程2x＋x=0，log2x=2－x，arccosx=x的实根依次为a，b，c，则a，b，c的从大到小的顺序为_______________________。
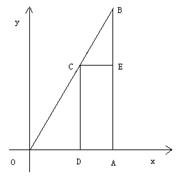
16，如图，Rt
OAB的三个顶点坐标分别为
O(0，0)，A(1，0) ，B(1，2)，在斜边OB上
任取一点C(x，2x) (0£x£2)，过C 作CD
OA于D，CE ^ AB于E，记 DODC的面积
为S1(x)，矩形CDAE的面积为S2(x)，DCEB
的面积为S3(x) 。对同一个 x，用f(x) 表示
S1(x)，S2(x)，S3(x)中的最大者，当C点在
线段OB上运动时，则f(x)的最小值为_____。
三，解答题。
17，已知z=cosq+(
－sin2q)i，(0£q<2p)，求z及argz的范围。
18，已知a>0，解关于x的不等式
>x－1。
19，在DABC，
=
=
，P为DABC为内切圆上的动点，求点P到顶点A，B，C的距离的平方和的最小值。
20，设0<x<1，0<y<1，
求证:
＋
＋
＋
³2
21，抛物线方程为x2=p(y＋1)(p>0)，直线l：y=x＋b与y轴的交点在抛物线准线的上方。
（1） 求证：直线l与抛物线总有两个交点；
（2） 设直线l与抛物线的交点为Q，R，且OQ^OR。求p关于b的函数表达式f(b)；
（3） 在（2）的条件下，若b变化，使得原点O到直线l的距离不大于
，求p的取值范围。