高三数学第三次月考

江苏省六合高级中学高三数学第三次月考　2006.1

一、选择题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一个是符合题目要求的)

1．设集合, ,　则A∩B=　　　　　　　　　　

A．　　　　　　　　　　　　　　　　　　　　　　B．

C．　　　　　　　　　　　　　　　D．

2．函数的定义域是

A. 　　　　B. 　　　　 C.　　　 D.

3． 在同一平面直角坐标系中，函数与的图象关于

A. 直线对称　　　 B.轴对称　　　 C. 轴对称　　 D.直线对称

4. 函数在下列哪个区间上是减函数　　　　　　　　　　　　　　

A．　　　　　 B．　　　　　　C．　　　　　　　D．

5.已知直线过点（－2，0），当直线与圆有两个交点时，其斜率k的取值范围是 A． B．　　　 C．　　　　 D．

6. 将函数的图象按向量平移后得到函数的图象，则向量可以是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

A．　　　　 B．　　　　 C．　　　　  D．

7.设m、n是两条不同的直线，是三个不同的平面，给出下列四个命题：

　　①若，，则　　　 　②若，，，则

　　③若，，则　　　 ④若，，则

　　其中正确命题的序号是(　　)

A. ①和②　　　 B. ②和③　　 　　C. ③和④　 　　  D. ①和④

8. 在正四面体P－ABC中，D，E，F分别是AB，BC，CA的中点，下面四个结论中不成立的是

　　A．　　BC//平面PDF　　　　  　 B．　　DF⊥平面PA E

　　C．　　平面PDF⊥平面ABC　 　 D．　平面PAE⊥平面 ABC

9. 在等比数列中，已知，则

A.　　　　　 B.　　　　 C.　　　　　 D.

10. 下列结论正确的是　　　　　　　　　　　　

　A．当　　　　　　　　B．

　C．的最小值为2　　　　　　　 D．当无最大值

11.椭圆的焦点为F₁、F₂，过点F₁作直线与椭圆相交，被椭圆截得的最短的线段MN长为，的周长为20，则椭圆的离心率为　　　　　

　　A．　　　　　　　B．　　　　　　　　 C．　　　　　　　　 D．

12.对任意实数，定义为不大于的最大整数（例如等），设函数，给出下列四个结论：①②③是周期函数④是偶函数。其中正确结论的个数是

A.1个　　　　　  B.2个　　　　　  C.3个　　　　　 D.4个

二、填空题：（本大题共4小题，每小题4分，共16分.把答案填在题中横线上.）

13．已知向量，且A、B、C三点共线，则k=　　 

14．若双曲线的右支上一点到直线的距离为，则的值＼

为　　　　  .

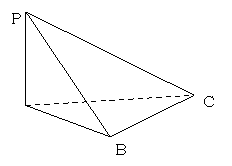15．如图，PA⊥平面ABC，∠ABC=90°且PA=AB=BC=a，则

异面直线PB与AC所成角的正切值等于_______　 _.

16．设函数 f(x)在 (－∞,+∞)内有定义，下列函数

A

(1) y=－();　　　 (2) y= (²);　

(3) y=－(－);　　　 (4) y=()－(－)

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  　　　　　　　　　　　中必为奇函数的有　　　　　　　 （要求填写正确答案的序号）

三、解答题：本大题共6小题，共74分. 解答应写出文字说明，证明过程或演算步骤.

17. （本小题满分12分）

已知在△ABC中，sinA（sinB＋cosB）－sinC＝0，　sinB＋cos2C＝0，

求角A、B、C的大小.

18．（本小题满分12分）

设平面内的向量, , ，点P是直线OM上的一个动点，求当取最小值时，的坐标及ÐAPB的余弦值

19．（本小题满分12分）

 已知数列的前项和为，数列满足：，前项和为，

设。

⑴ 求数列的通项公式；　　　　　　 ⑵ 求证：数列是单调递减数列

20．（本小题满分12分）

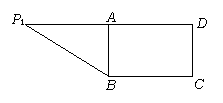
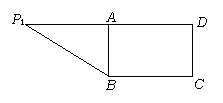
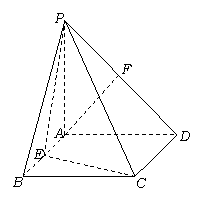
在直角梯形P₁DCB中，P₁D//CB，CD⊥P₁D且P₁D = 6，BC = 3，DC =，A是P₁D的中点，沿AB把平面P₁AB折起到平面PAB的位置，使二面角P－CD－B成45°角，设E、F分别是线段AB、PD的中点．

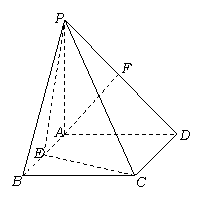　 （1）求证：AF//平面PEC；

　 （2）求平面PEC和平面PAD所成的二面角的大小；

　 （3）求点D到平面PEC的距离．

21．（本小题满分12分）

已知点N（1，2），过点N的直线交双曲线于A、B两点，且

　 （1）求直线AB的方程；

　 （2）若过N的直线l交双曲线于C、D两点，且，那么A、B、C、D四点是否共圆？为什么？

22．（本小题满分14分）

已知函数：

　⑴ 证明：对定义域内的所有都成立；

　⑵ 当的定义域为时，求证：的值域为；

　⑶ 设函数，求函数的最小值 。

江苏省六合高级中学高三数学第三次月考答案2006.1

DBCCC  DACBB　BC

13． 　　14．　　15．　　 16．（2）（4）

17．解法一　由

　　　 得

　　　 所以

　　　 即

　　　 因为所以，从而

　　　 由知 从而.

　　　 由

　　　 即

　　　 由此得所以

解法二：由

　　　 由、，所以

　　　 即

　　　 由得

　　　 所以

　　　 即 　　　　　　因为，所以

　　　 由从而，知B+2C=不合要求.

　　　 再由，得　所以

18．解　 设．

∵　点P在直线OM上，

∴　与共线，而，

∴　x－2y=0即x=2y，有．　　　　 

∵　，，

∴　

= 5y²－20y+12

= 5(y－2)²－8．　　　　　　　　　　　　

从而，当且仅当y=2，x=4时，取得最小值－8，此时，，．

于是，，，

∴　．

19．⑴ ，当时，

　　 ∴

⑵

　 ∵

　 ∴数列是单调递减数列

20．①取PC中点M，连结FM、EM

//

　∵  F、M分别为PD、PC中点

//

　∴  FM＝CD

//

　∵  E为AB中点，∴ AE＝CD

　∴  FM＝AE，　　∴FMEA为平行四边形

　∴  AF//EM

　∵  AF平面PEC，EM平面PEC

　∴　AF//平面PEC

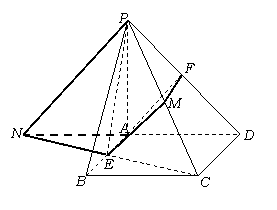
②延长DA，CE交于点N，连结PN

　

//

∵　AE//CD　 且E为AB中点

　∴  AE＝CD　 ∴AE为△NDC的中位线

　∴  AN＝AD＝PA　∴△PND为Rt△

　　  又　NE＝EC＝　PE＝

　　　∴　△PNC为Rt△

　　　∴　PC⊥PN  PD⊥PN

　　　∴　∠CPD为平面PEC和平面PAD所成二面角的平面角

　　　又　PD＝　　 CD＝　　PD⊥DC

　　　∴　tan∠CPD＝＝＝

　　　∴　∠CPD＝30°

　　　∴　平面PEC和平面PAD所成二面角为30° …………………………………8’

　　③连结ED

　　　∵　PA⊥平面ABCD

　　　∴　V_P－CED＝S_△CED·PA＝＝

　　　　  V_P－CED＝V_D－PCE＝

　　　设点D到平面PCE的距离为d．

　　　　  S_△PCE＝

　　　　  V_P－PCE＝S_△DCE·d＝

　　　∴　d＝

　　　点D到平面PEC的距离为．

21．（1）设直线AB：代入得

　　 　 　　（＊）

　　　　令A（x₁，y₁），B（x₂，y₂），则x₁、x₂是方程的两根

　　　  ∴　 且 　 

　　　  ∵　　 ∴　N是AB的中点　 ∴

　　　  ∴　　　k = 1　　∴AB方程为：y = x + 1  

　 （2）将k = 1代入方程（＊）得　 或 

　　　　由得，

　　　  ∴　，

　　　  ∵　　　∴　CD垂直平分AB　　∴　CD所在直线方程为

　　　　即代入双曲线方程整理得

　　　　令，及CD中点

　　　　则，，　∴，　

　　　　CD =，

　　　　，即A、B、C、D到M距离相等

　　　  ∴　A、B、C、D四点共圆　　　 12分

22．⑴ 证明：

　 ∴结论成立　　　

⑵ 证明：

当

　　即　　　　　　　　　　  　　 

⑶ 解：　

① 当

如果　即时，则函数在上单调递增

　

如果

当时，最小值不存在　　　　　　　　　　　　 

② 当　

如果

如果　 …13分

当

综合得：当时　g（x）最小值是

当时　g（x）最小值是　　  当时　g（x）最小值为

当时　g（x）最小值不存在