高二数学
第二学期期中考试试题
普高卷 时量：100分钟 满分：100分
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | |||||
| 得分 | |||||||||
一、选择题（3’×12=36’）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1．下列说法正确的是 。
A．直线a平行于平面M，则a平行于M内的任意一条直线
B．直线a与平面M相交，则a不平行于M内的任意一条直线
C．直线a不垂直于平面M，则a不垂直于M内的任意一条直线
D．直线a不垂直于平面M，则过a的平面不垂直于M
2．设P是平面α外一点，且P到平面α内的四边形的四条边的距离都相等，则四边形是 。
A．梯形 B．圆外切四边形 C．圆内接四边形 D．任意四边形
3．平面α与正四棱柱的四条侧棱AA1、BB1、CC1、DD1分别交于E、F、G、H.若AE=3，BF=4，CG=5，则DH等于 。
A．6 B．5 C．4 D．3
4．二面角α—EF—β是直二面角，C∈EF，AC 
α，BCβ,∠ACF=30°,∠ACB=60°，则cos∠BCF等于 。
A．
B．
C．
D．
|
|
D’ C’5．正方体ABCD-A’B’C’D’中，面对角线BC’与对角面BB’D’D所成的角为
，则tan= 。
A． 1 B．
C． D． 
6．
＝
＝4，〈，〉＝60°，则－＝ 。
A. 4 B. 8 C. 37 D. 13
|
D’ |
P7．若＝（2,-3,1）,＝(2,0,3)，
＝(0,2,2)，则
（＋）＝ 。
A. 4 B. 15 C. 7 D. 3
8．如图，棱锥P-ABCD的高PO＝3，截面积A’B’C’D’平行于底面ABCD，PO与截面交于O’，且OO’＝2。如果四边形ABCD的面积为36，则四边形A’B’C’D’的面积为 。
A. 12 B. 16 C. 4 D. 8
9．球的体积是
π，则此球的表面积是 。
A. 12π B. 16π C. 
π D. 
π
10．已知AB是异面直线a、b的公垂线段，AB=2，且a与b成30°角，在直线a上取AP=4，则点P到直线b的距离为 。
A．
B．4 C．2
D．或2
11．一个棱柱是正四棱柱的条件是 。
A.底面是正方形，有两个侧面是矩形
B.底面是正方形，有两个侧面垂直于底面
C.底面是菱形，且有一个顶点处的三条棱两两垂直
D.每个侧面都是全等矩形的四棱柱
12．三棱柱
中，M、N分别是
、
的中点，设
，
，
，则
等于 。
A．
B．
C．
D．
二、填空题（3’×4=12’）
13．边长为2的正方形ABCD在平面α内的射影是EFCD，如果AB与平面α的距离为
，则AC与平面α所成角的大小是
。
14．球的半径为8，经过球面上一点作一个平面，使它与经过这点的半径成45°角，则这个平面截球的截面面积为 。
15．已知＝（—4,2,x），＝(2,1,3),且⊥，则x＝ 。
16．已知a、b是直线，、
、
是平面，给出下列命题：
①若∥，a，则a∥
②若a、b与所成角相等，则a∥b
③若⊥、⊥，则∥ ④若a⊥, a⊥，则∥
|
E D A
C B |
N M其中正确的命题的序号是________________。
三、解答题（10’＋10’＋10’＋12’＋12’=52’）
17．已知四棱锥S—ABCD中，底面为正方形，SA⊥底面ABCD，且AB＝SA＝2，M、N分别是AB、SC的中点. ①求证：AB⊥MN；②求异面直线AB与SC的的距离。
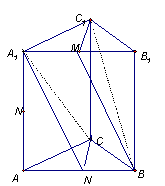18．已知直三棱柱ABC—A1B1C1中，M、N分别为A1B1、AB的中点. ①求证：BM∥平面A1NC；
② 求证：平面A1NC∥平面BMC1 。
19．已知在平行四边形ABCD中，AB=30，AD=50，DB=40，
以BD为棱折成1200的二面角。
（1） 求点A到平面BCD的距离
（2）
求
的长。
|
D A
C B |
20．已知四棱锥P-ABCD的底面ABCD是AB=2，BC=的矩形，侧面PAB是等边三角形，且侧面PAB⊥底面ABCD。
（1） 证明：BC⊥侧面PAB
（2） 证明：侧面PAD⊥侧面PAB
（3） 求侧面PBC与侧面PAD所成的角的大小。
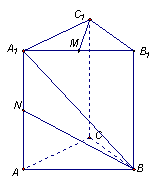
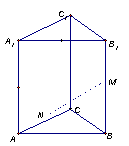
21．如图：直三棱柱，底面三角形ABC中，
，
，棱
，M、N分别是
、
的中点。
①求
的长； ②求
的值；
③求证：