命题人:刘锡亮 校对:刘岩
1、集合A={1,2},B={1,3,5},则![]() 等于
( )
等于
( )
A {1} B {1,2} C {1,3,5} D ![]()
2、不等式![]() 的解集是
( )
的解集是
( )
A (-1,3) B (1,3) C (-3,1) D (-2,3)
3、集合A={x3+2x-x2>0},B={xx>a},若A![]() B,则a的范围是(
)
B,则a的范围是(
)
A a≤-1 B a≥3 C a<-1 D -3<a<3
4、命题p:1>2,命题q:{2}![]() {2,3},则下列判断①p或q为真命题,②p且q为假命题,③非p为真命题,这三个判断中正确的有( )
{2,3},则下列判断①p或q为真命题,②p且q为假命题,③非p为真命题,这三个判断中正确的有( )
A 0个 B 1个 C 2个 D 3个
5、函数![]() 的图象不经过
( )
的图象不经过
( )
A第一象限 B第二象限 C第三象限 D第四象限
6、已知a、b、a+b成等差,a、b、ab成等比,且![]() ≤1,则m的取值范围为
( )
≤1,则m的取值范围为
( )
A(1,+![]() )
B
)
B ![]() C
C![]() D
D![]()
7、若方程![]() 有正数解,则实数
有正数解,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、等差数列{an},Sn是前n项和,已知a1>0,且S3=S11 ,则使Sn取最大值时n的值为 A 5 B 7 C 9 D 11
9、递减等差数列{an}满足a1+a3+a5=6,a1a3a5=0,若![]() ,则b4=
,则b4=
A
![]() B 2
C 4
D 16
B 2
C 4
D 16
10、![]() 在[0,2]上为减函数,则
( )
在[0,2]上为减函数,则
( )
A a>2 B
a<0
C 0<a<![]() D
0<a<2
D
0<a<2
11、已知奇函数f(x)在(-∞,0)为减函数,且f(2)=0,则不等式(x-1)f(x-1)>0的解集为( )
A.{x-1<x<1或1<x<3} B.{x-3<x<1或x>2}
C.{x-3<x<0或x>3} D. {x-3<x<-1}
12、已知![]() ,有以下四个结论
,有以下四个结论
①![]() 的图象关于原点对称,②
的图象关于原点对称,②![]() 在R上是增函数,③
在R上是增函数,③![]() ,④
,④![]() 有最小值0 其中正确的结论有 ( )
有最小值0 其中正确的结论有 ( )
A 1个 B 2个 C 3个 D 4个
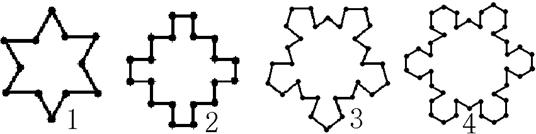
13、如图,第n个图形是由正n+2边形“扩展”而来,(n=1、2、3、…)则在第n个图形中共有___________个顶点。
14、设函数f(n)=k(其中n∈N+),k是![]() 的小数点后的第n位数字,
的小数点后的第n位数字,![]() = 1.…,则
= 1.…,则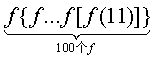 = ________
= ________
15、定义在R上的偶函数![]() 满足
满足![]() ,且在[-1,0]上单调递增,则①
,且在[-1,0]上单调递增,则①![]() ,②
,②![]() 在[0,1]上递增,③
在[0,1]上递增,③![]() 在[1,2]上递减,④
在[1,2]上递减,④![]() 是周期函数,⑤
是周期函数,⑤![]() 图象关于直线x=1对称。
图象关于直线x=1对称。
以上正确的是_________________ (漏选、错选均不得分)
16、已知函数![]() 满足
满足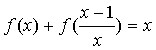 ,则函数
,则函数![]() =_______
=_______
17、(12分)已知![]()
(1)求![]() 的反函数
的反函数![]()
(2)求![]() 的值域
的值域
18、(12分) ![]() 是定义在
是定义在![]() 上的增函数,且
上的增函数,且![]()
(1)求![]() 的值
的值
(2)若![]() ,解不等式
,解不等式![]()
19、20、21、22题在答题纸上
鸡西市第一中学高三第二次考试数学答题卡
一、
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
二、
13、_________________14、____________________
15、_________________16、____________________
17、
18、
19、(12分)设函数![]() ,
,
(1) 证明:对一切![]() ,f(x)+f(1-x)是常数;
,f(x)+f(1-x)是常数;
(2)记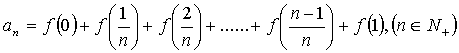 ,求
,求![]() ,并求出数列{an}的前n项和。
,并求出数列{an}的前n项和。
20、(12分) 已知函数f(t)=log2t,t∈[![]() ,8]
,8]
(1)求f(t)的值域G;
(2)若对于G内的所有实数x,不等式-x2+2mx-m2+2m≤1恒成立,求实数m的取值范围。
21、(12分)已知等差数列{an}中,a1=1,公差d>0,且a2、a5、a14分别是等比数列{bn}的第二项、第三项、第四项。
(1)求数列{an}、{bn}的通项an、bn ;
(2)设数列{cn}对任意的n∈N*,均有![]() +…+
+…+![]() =an+1成立,求c1+c2+…+c2005的值.
=an+1成立,求c1+c2+…+c2005的值.
22、(14分) 已知圆O,由圆心O出发的n(n≥2,n![]() )条射线将圆均分成n个扇形,现将这n个扇形涂色,要求每个扇形只能用一种颜色涂,且相邻的扇形所涂颜色不相同(有公共边的扇形叫相邻扇形),有5种颜色可供选择(这5种颜色中同一种颜色可以使用一次或多次也可以一次都不用),这样得到的不同涂法有
)条射线将圆均分成n个扇形,现将这n个扇形涂色,要求每个扇形只能用一种颜色涂,且相邻的扇形所涂颜色不相同(有公共边的扇形叫相邻扇形),有5种颜色可供选择(这5种颜色中同一种颜色可以使用一次或多次也可以一次都不用),这样得到的不同涂法有![]() 种。特别定义a1=5
种。特别定义a1=5
(1)求出a2、a3、a4.
(2)若an=5![]() 4n-1-an-1(n≥3,n
4n-1-an-1(n≥3,n![]() ),求证
),求证![]() ( n≥2,n
( n≥2,n![]() )为等比数列.
)为等比数列.
(3)求an(n≥2,n![]() )的通项公式。
)的通项公式。
ABADA BDBBC AC
13 (n+2)(n+3) 14 4 15 145 16![]()
17、解:设t=x2+2,∴t≥2
∵![]() ,∴
,∴![]() (
(![]() ≥2)
≥2)
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,(x≥2)
,(x≥2)
![]() =
=![]() (2x-1≥2且x≥2)
(2x-1≥2且x≥2)
=![]() ,
,![]() ≥4 ∴
≥4 ∴![]()
18、∵![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]() ∴
∴![]()
![]()
![]()
19、解:∵![]() , ∴
, ∴![]() =
=![]()
![]()
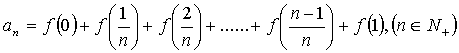
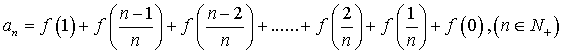 ∴2
∴2![]() =
=![]() ∴
∴![]() =
=![]() ∴Sn=
∴Sn=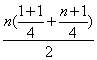 =
=![]()
20、解:(Ⅰ)∵f(t)=log2t在t∈[![]() ]上是单调递增的,∴log2
]上是单调递增的,∴log2![]() ≤log2t≤log28.
≤log2t≤log28.
即![]() ≤f(t)≤3. ∴f(t)的值域G为[
≤f(t)≤3. ∴f(t)的值域G为[![]() ] ……4分
] ……4分
(Ⅱ)由题知—x2+2mx—m2+2m≤1在x∈[![]() ]上恒成立
]上恒成立
![]() x2-2mx+m2-2m+1≥0在x∈[
x2-2mx+m2-2m+1≥0在x∈[![]() ]上恒成立. ……1分
]上恒成立. ……1分
令g(x)=x2-2mx+m2-2m+1,x∈[![]() ].
].
只需g min(x)≥0即可.
而g(x)=(x-m)2-2m+1,x∈[![]() ].
].
(1)
当m≤![]() 时,g min(x)=g(
时,g min(x)=g(![]() )=
)=![]() -3m+m2+1≥0.∴4m2-12m+5≥0.
-3m+m2+1≥0.∴4m2-12m+5≥0.
解得m≥![]() 或m≤
或m≤![]() ∴m≤
∴m≤![]() ……2分
……2分
(2)
当![]() <3时,g min(x)=g(m)=-2m+1≥0.
<3时,g min(x)=g(m)=-2m+1≥0.
解得m≤![]() 这与
这与![]() <m<3矛盾
……2分
<m<3矛盾
……2分
(3)
当m≥3时,g min(x)=g(3)=10+m2-8m≥0.解得m≥4+![]() 或m≤4-
或m≤4-![]() .
.
而m≥3,∴m≥4+![]() . ……2分
. ……2分
综上,实数m的取值范围是(-∞,![]() ]∪[4+
]∪[4+![]() ,+∞). ……1分
,+∞). ……1分
21.解:(Ⅰ)由题意,有 (a1+d)(a1+13d)=(a1+4d)2. ……2分
而a1=1,d>0.∴d=2,∴an=2n-1. ……3分
公比q=![]() =3,a2=b2=3. ∴bn=b2·qn-2=3·3 n-2=3
n-1. ……2分
=3,a2=b2=3. ∴bn=b2·qn-2=3·3 n-2=3
n-1. ……2分
(Ⅱ)当n=1时,![]() =a2,∴c1=1×3=3.当n≥2时,∵
=a2,∴c1=1×3=3.当n≥2时,∵![]() ……①
……①
![]() ……②
……②
②—①,得![]() ∴cn=2bn=
∴cn=2bn= ![]()
∴cn=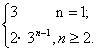 ……4分
……4分
∴c1+c2+c3+…+c2005=3+2(31+32+33+…+32004) =3+2·![]() ……2分
……2分
22.a2=20,a3=60、a4. =260
∵an=5![]() 4n-1-an-1(n≥3,n
4n-1-an-1(n≥3,n![]() )
)
∴![]() =-
=-![]() (
(![]() )
)
∴![]() (n≥2,n
(n≥2,n![]() )
)