黄冈市2005年秋期末调考试题
数 学（文科）
命题人：蕲春一中 宋春雨
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分，考试时间120分钟.
第Ⅰ卷（选择题 共60分）
一.选择题：（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的．请把所选项前的字母填在答题卷的表格内）
1.下列函数中，图象关于直线
对称的是
A
B
C
D
2.设集合M={x x2-2x<0,x∈R},N={x x<2,x∈R},则
A．M∪N=M B．M∩N=M C．()∩N=φ D．()∩N=R
3.给出两个命题：p:x=x的充要条件是x为正实数；q:存在反函数的函数一定是单调函数，则下列复合命题中真命题是
A．p且q B．p或q C．¬p且q D．¬p或q
4.由数字1,2,3,…,9组成的三位数中,各位数字按严格递增(如“156”)或严格递减(如“421”)顺序排列的数的个数是
A．120 B．168 C．204 D．216
5. 已知四边形ABCD是菱形，点P在对角线AC上（不包括端点A，C），则
等于
A．
B．
C．
D．
6.已知
是
上的单调增函数，则
的范围
A．
或
B．b≤-1或b≥2
C．
D．-1≤b≤2
7. 原点和点（1，1）在直线x+y－a=0两侧，则a的取值范围是
A．a<0或a>2 B．a=0或a=2 C．0<a<2 D．0≤a≤2
8. 若圆x2+y2=r2(r>0)至少能盖住函数
的一个最大值点和一个最小值
点，则r的取值范围是
A．
B．
C．
D．以上都不对
9．若数列
的通项公式为an=5()2n-2-4()n-1(n∈N*),{an}的最大项为第
项，最小项为第
项，则
等于
A．3 B．4 C．5 D．6
10.如果直线y=kx+1与圆x2+y2+kx+my-4=0交于M、N两点，且M、N关于直线x+y=0对称，则不等式组：表示的平面区域的面积是
A． B． C． D．1
11.过抛物线
的焦点作直线交抛物线于
，
、
，
两点，若
，则
等于
A．4p B．5p C．6p D．8p
12. 4只笔与5本书的价格之和小于22元，而6只笔与3本书的价格之和大于24元，则2只笔与3本书的价格比较
A．2只笔贵 B．3本书贵 C．二者相同 D．无法确定
黄冈市2005年秋期末调考试题
数 学（文科）
第Ⅱ卷（非选择题 共90分）
一.选择题答案卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二.填空题(每小题4分,共16分)
13.若在
的展开式中
的系数为
，则
.
14.已知函数f(x)＝，若方程f(x)＝－2x有两个相等的实根，则函数解析式为 ．
15.若双曲线的一条准线恰为圆x2+y2+2x=0的一条切线,则k等于_____.
16.设函数f(x)=xx+bx+c,给出下列命题：
①b=0, c>0 时，方程f(x)=0只有一个实数根；②c=0时，y=f(x)是奇函数；
③y=f(x)的图象关于点（0，c）对称；④方程f(x)=0至多有两个实根.
上述四个命题中所有的正确命题的序号为 .
三.解答题
17.已知向量=（sinB，1－cosB)，且与向量=（2，0）所成角为
，其中A, B, C是△ABC的内角． （1）求角Ｂ的大小；
（2）求sinA+sinC的取值范围．((本题满分12分))
18. (1)已知=4，=3，（2－3）·（2+）=61，求与的夹角θ；
(2)设=（2，5），=（3，1），=（6，3），在上是否存在点M，使
⊥，若存在，求出点M的坐标，若不存在，请说明理由. (本题满分12分)
19.某学生语文、数学、英语三科考试成绩，在本次调研考试中排名全班第一的概率:语文为0.9，数学为0.8，英语为0.85，问这次考试中
（1）该生三科成绩均未获得第一名的概率是多少？
（2）该生恰有一科成绩未获得第一名的概率是多少? (本题满分12分)
20.若函数y=f(x)是周期为2的偶函数,当x∈[2,3]时,f(x)=x-1,在y=f(x)的图象上有两点A、B,它们的纵坐标相等,横坐标都在区间[1,3]上,定点C的坐标为(0,a)(其中2＜a＜3),求△ABC面积的最大值.(本题满分12分)
21.已知函数f(x)=logax(a>0且a≠1),若数列：2, f(a1), f(a2),…, f(an), 2n+4(n∈N*)成等差数列.
(1) 求数列{an}的通项an；
(2) 若0<a<1，数列{an}的前n项和为Sn,求Sn；
(3) 若a=2，令bn=an·f(an)，试比较bn+1与bn的大小.(本题满分12分)
22. 已知ΔOFQ的面积为2,且·=m .
(1)设＜m＜4,求向量与的夹角θ正切值的取值范围；
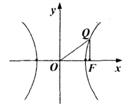(2)设以O为中心，F为焦点的双曲线经过点Q（如图),=c,m=(-1)c2,当取得最小值时，求此双曲线的方程.(本题满分14分)
黄冈市2005年秋期末调考试题
数 学（文科）参考答案
第Ⅱ卷（非选择题 共90分）
一.选择题 BBDBA DCBAC AA
二.填空题
13. -2 14. f(x)= 15. 48 16.①②③)
三.解答题
17.解：（1）∵=（sinB，1-cosB) ,与向量=（2，0）所成角为
∴
……………………………………………………………3分
∴tan
…………………6分
（2）：由（1）可得∴
……………………………………8分
∵
∴
……………………………………………………………………10分
∴
当且仅当
…………………………………12分
18.（1）∵（2
－3
）·（2+）=61，∴
…2分
又=4，=3，∴·=－6.…………………………………………4分.
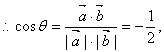………………………………………………5分
∴θ=120°.………………………………………………………………6分
（2）设存在点M，且
…………………………8分
∴存在M（2，1）或
满足题意.……………………12分.
19.解：分别记该生语、数、英考试成绩排名全班第一的事件为A、B、C，则P（A）=0.9
P（B）=0.8，P（C）=0.85 …………………………2分
（1）
=[1－P（A）]·[1－P（B）]·[1－P（C）]
=（1－0.9）×（1－0.8）×（1－0.85）=0.003
答：该生三科成绩均未获得第一名的概率是0.003………………6分
（2）P（
）
= P（
=
=[1－P（A）]·P（B）·P（C）+P（A）·[1－P（B）]·P（C）+P（A）·P（B）·[1－P（C）]
=（1－0.9）×0.8×0.85+0.9×（1－0.8）×0.85+0.9×0.8×（1－0.85）
=0.329
答：该生恰有一科成绩未获得第一名的概率是0.329……………………12分
20.∵f(x)是以2为周期的周期函数,当x∈[2,3]时,f(x)=x-1,
∴当x∈[0,1] 时,f(x)=f(x+2)=(x+2)-1=x+1.…………………………3分
∵f(x)是偶函数,∴当x∈[-1,0]时,f(x)=f(-x)=-x+1,
当x∈[1,2]时,f(x)=f(x-2)=-(x-2)+1=-x+3.……………………………6分
设A、B的纵坐标为t(1≤t≤2),并设A在B的左边,则A、B的横坐标分别为
3-t,t+1.则AB=(t+1)-(3-t)=2t-2,△ABC的面积为S=·(2t-2)·(a-t)
=-t2+(a+1)t-a=-(t-)2+ ……………………………………9分
∵2＜a＜3,∴＜＜2,∴当t=时,S有最大值.………12分
21.(1)∵2n+4=2+(n+2-1)d, ∴d=2,∴f(an)=2+(n+1-1)·2=2n+2, ∴an=a2n+2.………3分
(2)Sn== .…………………………………………………7分
(3)∵bn=an·f(an)=(2n+2)a2n+2=(2n+2)·22n+2=(n+1)·22n+3 ,
∴= ·4＞1,∴bn+1＞bn.………………………………………………12分
22.(1)∵,∴tanθ=.
又∵＜m＜4,∴1＜m＜4.………………………………6分
(2)设所求的双曲线方程为(a＞0,b＞0),Q(x1,y1),
则=(x1-c,y1),∴S△OFQ= ·y1=2,∴y1=±.
又由·=(c,0)·(x1-c,y1)=(x1-c)c=(-1)c2,∴x1=c.…………8分
∴==≥.
当且仅当c=4时, 最小,这时Q点的坐标为(,)或(,-).……12分
∴, ∴.
故所求的双曲双曲线方程为.…………………………………14分