东北师大附中高三年级第二次摸底考试理科数学试题

03—04年东北师大附中高三年级第二次摸底考试理科数学试题

一、选择题（每题只有一个正确答案，每小题5分，共60分）

1．已知集合，则实数a的取值

　 范围是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．[1，2]　　　　　　　　B．（－1，2）　　　　　C．[－1，2]　　　　　　 D．（－2，1）

2．sin2490°=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．－　　　　　　　　　B．　　　　　　　　　　　C．－　　　　　　　　D．

3．在数列，则该数列中相邻两项的乘积是负数的

　 是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　 B．a₂₂·a₂₃　　　　　　　　 C．a₂₃·a₂₄　　　　　　　　D．a₂₄·a₂₅

4．要使函数上存在反函数，则a的取值范围是　　　　　　　　　（　　）

　　　 A．　　　　　　　　 B．　　　　　　　　C．或　　D．

5．2的必要非充分条件是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　B．　　　　　C．　　　　　D．

6．已知椭圆和抛物线的离

　 心率分别为e₁、e₂、e₃，则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．e₁e₂> e₃　　　　　　　 B．e₁e₂= e₃　　　　　　　 C．e₁e₂< e₃　　　　　　　 D．e₁e₂≥e₃

7．已知长方体ABCD－A₁B₁C₁D₁中，AB=BC=4，CC₁=2，则直线BC₁和平面DBB₁D₁所成

　 角的正弦值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　 B．　　　　　　　　　 C．　　　　　　　　 D．

8．函数在闭区间[－1，1]上的最大值是　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　B．　　　　　　　　　　C．0　　　　　　　　　　　　D．－

9．随机变量ξ的概率分布规律为其中a是常数，则

　 的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　B．　　　　　　　　　　　C．　　　　　　　　　　　D．

10．设a、b是方程的两个不相等的实数根，那么过点A（a,a²）和

　　B（b，b²）的直线与圆的位置关系是　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．相离　　　　　　　　　 B．相切　　　　　　　　　 C．相交　　　　　　　　　 D．随θ的值变化而变化

11．对于项式，四位同学作出了四种判断：

①存在n∈N₊，展开式中有常数项；

②对任意n∈N₊，展开式中没有常数项；

③对任意n∈N₊，展开式中没有x的一次项；

④存在n∈N₊，展开式中有x的一次项.

上述判断中正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．①与③　　　　　　　 B．②与③　　　　　　　　C．②与④　　　　　　　 D．④与①

12．已知定义在R上的函数y=f(x)满足下列三个条件：①对任意的x∈R都有②对于任意的，都有③的图象关于y轴对称，则下列结论中，正确的是　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　 B．

　　　 C．　　　　　　　　　 D．

二、填空题（每小题4分，共16分）

13．当=　　　　　　　　  .

14．不等式的解集为　　　　　　　　 .

15．设非零复数x，y满足，则代数式的值是　　　　 .

16．若实数x、y满足的最大值为　　　　　　  .

三、解答题（本大题共6小题，共74分）

17．（本题满分12分）

某人忘记了电话号码的最后一个数字，因而他随意地拨号，假设拨过了的号码不再重复，试求下列事件的概率：

　 （1）第3次拨号才接通电话；

　 （2）拨号不超过3次而接通电话.

18．（本题满分12分）

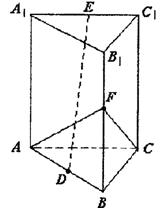
如图，正三棱柱AC₁中，AB=2，D是AB的中点，E是A₁C₁的中点，F是B₁B中点，异面直线CF与DE所成的角为90°.

　 （1）求此三棱柱的高；

　 （2）求二面角C—AF—B的大小.

19．（本题满分12分）

已知向量=（2，2），向量与向量的夹角为，且·=－2，

　 （1）求向量；

　 （2）若，其中A、C是△ABC的内角，若三角形的三内角A、B、C依次成等差数列，试求+的取值范围.

20．（本题满分12分）

某医药研究所开发一种新药，如果成人按规定的剂量服用，据监测：服药后每毫升血液中的含药量y与时间t之间近似满足如图所示的曲线.

　 （1）写出服药后y与t之间的函数关系式；

　 （2）据测定：每毫升血液中含药量不少于4微克时治疗疾病有效，假若某病人一天中第一次服药时间为上午7:00，问一天中怎样安排服药的时间（共4次）效果最佳？

21．（本题满分12分）

如图，过点（1，0）的直线l与中心在原点，焦点在x轴上且离心率为的椭圆相交于A、B两点，直线过线段AB的中点M，同时椭圆上存在一点与右焦点F关于直线l对称，求直线l和椭圆的方程.

22．（本题满分14分，附加题4分）

　 （Ⅰ）已知a>0，函数

　 （1）当b>0时，若对任意；

　 （2）当b>1时，证明：对任意的充要条件是；

　 （Ⅱ）（本小题为附加题，如果解答正确加4分，但全卷总分不超过150分）

已知a>0，函数.当时，讨论：对任意的充要条件.