人造卫星宇宙速度
1．近地卫星线速度为7．9 km/s，已知月球质量是地球质量的1/81，地球半径是月球半径的3．8倍，则在月球上发射“近月卫星”的环绕速度约为（ ）
A．1．0 km/s B．1．7 km/s
C．2．0 km/s D．1．5 km/s
【解析】 卫星在地球（月球）表面附近绕地球（月球）做匀速圆周运动，向心力为地球（月球）对卫星的吸引力，则G
近地（月）卫星的线速度为v＝
近月卫星与近地卫星的线速度之比为
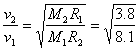＝0．22
所以近月卫星的线速度为v2＝0．22v1＝0．22×7．9 km/s＝1．7 km/s
选项B正确．
【答案】 B
2．一颗人造地球卫星在离地面高度等于地球半径的圆形轨道上运行，其运行速度是地球第一宇宙速度的________倍．
【解析】 由G
，得v星＝
，而第一宇宙速度为近地轨道卫星的线速度，由G
，故卫星的速度是第一宇宙速度的
倍．
【答案】
3．假如一做圆周运动的人造地球卫星的轨道半径增大到原来的2倍，仍做圆周运动，则
（ ）
A．根据公式v＝ωr，可知卫星运动的线速度将增大到原来的2倍
B．根据公式F＝mv2/r，可知卫星所需的向心力将减小到原来的1/2
C．根据公式F＝GMm/r2，可知地球提供的向心力将减小到原来的1/4
D．根据上述B和C中给出的公式，可知卫星运动的线速度将减小到原来的
/2
【解析】 卫星绕地球做圆周运动时，地球对卫星的吸引力提供卫星做圆周运动的向心力，由F向＝G
知，卫星的轨道半径增大到原来的2倍，向心力减小到原来的
，C选项正确．根据G＝m
得v＝
所以，卫星的轨道半径增大到原来的2倍，线速度减小到原来的．D选项正确．
由于随着半径r的变化，角速度和线速度都要变化，所以不能根据v＝ω r和F＝m得出v∝r及F∝
，故A、B选项均错．
【答案】 CD
4．关于绕地球做匀速圆周运动的人造地球卫星，以下判断正确的是（ ）
A．同一轨道上，质量大的卫星线速度大
B．同一轨道上，质量大的卫星向心加速度大
C．离地面越近的卫星线速度越大
D．离地面越远的卫星线速度越大
【解析】 绕地球做匀速圆周运动的卫星，向心力为地球对卫星的万有引力，则
卫星的向心加速度为a＝
所以，卫星的向心加速度与地球的质量及轨道半径有关，与卫星的质量无关，B选项错．
卫星的线速度为v＝
则卫星的线速度与地球质量和轨道半径有关，与卫星质量无关，轨道半径越小，卫星的线速度越大，所以A、D选项错，C选项正确．
【答案】 C
5．两颗人造卫星绕地球做匀速圆周运动，周期之比为TA∶TB＝1∶8，则轨道半径之比和运动速率之比分别为（ ）
A．RA∶RB＝4∶1；vA∶vB＝1∶2
B．RA∶RB＝4∶1；vA∶vB＝2∶1
C．RA∶RB＝1∶4；vA∶vB＝1∶2
D．RA∶RB＝1∶4；vA∶vB＝2∶1
【解析】 由GMm/R2＝4π2mR/T2，得R＝
，则A、B两颗人造地球卫星的轨道半径之比为
RA／RB＝
∶
＝1∶4．
由GMm/R2＝mv2／R得
v＝
则A、B两颗人造地球卫星的速率之比为
vA∶vB＝
∶
＝2∶1．
【答案】 D
6．人造地球卫星运行时，其轨道半径是月球轨道半径的1/3，则此卫星的周期大约是（ ）
A．1天到4天之间 B．4天到8天之间
C．8天到16天之间 D．大约是16天
【解析】 由GMm/r2＝4π2mr/T2得
T＝2π
则卫星与月球的周期之比为
T星/T月＝
＝1／3
则卫星的周期为T星＝T月/3＝5．77 d．
【答案】 B
7．一地球卫星高度等于地球半径，用弹簧秤将一物体悬挂在卫星内．物体在地球表面受的重力为98 N，则它在卫星中受地球的引力为________N，物体的质量为________kg，弹簧秤的读数为________N．
【解析】 在地球表面上：mg＝G
＝98 N，
在卫星中：mg′＝G
，
所以mg′＝24．5
N，物体质量不随位置变化，故m＝
＝10 kg，在卫星内的物体处于完全失重状态，故弹簧秤示数为零．
【答案】 24．5；10；0
8．如图6—5—4所示，有A、B两个行星绕同一恒星O做匀速圆周运动，运转方向相同，A行星的周期为TA，B行星的周期为TB，在某一时刻两行星第一次相遇（即两行星的距离最近），则（ ）
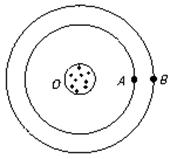
图6—5—4
A．经过时间t＝TA+TB，两行星第二次相遇
B．经过时间t＝
，两行星第二次相遇
C．经过时间t＝
，两行星第一次相距最远
D．经过时间t＝
，两行星第一次相距最远
【解析】 由于A在内侧离恒星近，故TA＜TB．第二次相遇时A比B多转一圈，即:
2π－
2π＝2π，也即:t（
）＝1 故t＝．而第一次相距最远，则A比B多转半圈，即:
t（）＝0．5
t＝ 选项B、D正确．
【答案】 BD
9．据观测，某行星外围有一模糊不清的环，为了判断该环是连续物还是卫星群，又测出了环中各层的线速度v的大小与该层至行星中心的距离R，则以下判断中正确的是（ ）
A．若v与R成正比，则环是连续物
B．若v与R成反比，则环是连续物
C．若v2与R成正比，则环是卫星群
D．若v2与R成反比，则环是卫星群
【解析】 若环为连续物，则角速度ω一定，由v＝Rω知，v与R成正比，所以A选项正确．若环为卫星群，由G
得v＝
所以，v2与R成反比，D选项正确．
【答案】 AD
10．地球同步卫星到地心的距离r可由r3＝
求出，已知式中a的单位是m，b的单位是s，c的单位是m/s2，则（ ）
A．a是地球半径，b是地球自转的周期，c是地球表面处的重力加速度
B．a是地球半径，b是同步卫星绕地心运动的周期，c是同步卫星的加速度
C．a是赤道周长，b是地球自转周期，c是同步卫星的加速度
D．a是地球半径，b是同步卫星绕地心运动的周期，c是地球表面处的重力加速度
【解析】 由G
，
及mg＝G得r3＝
，
故AD两项正确．
【答案】 AD
11．用m表示地球同步通讯卫星的质量，h表示它距地面的高度，R0表示地球的半径，g0表示地球表面处的重力加速度，ω0表示地球自转的角速度，则卫星所受地球对它的万有引力（ ）
A．等于零
B．等于mω02（R0+h）
C．等于m
D．以上结果都不对
【解析】 地球表面的重力加速度为
g0＝GM／R02
则卫星所受的地球对它的万有引力为
F＝GMm/（R0＋h）2＝mω02（R0+h）
得R0＋h＝
＝
，
由F＝mω02（R0＋h）得卫星所受的万有引力为
F＝mω02·＝m
．
【答案】 BC
12．设地面附近重力加速度为g0，地球半径为R0，人造地球卫星的圆形轨道半径为R，那么以下说法正确的是（ ）
A．卫星在轨道上向心加速度大小为g0·R02／R2
B．卫星运行的速度大小为
C．卫星运行的角速度大小为
D．卫星运行的周期为
【解析】 卫星在轨道上的向心加速度即为轨道上的重力加速度，有
ma＝GMm/R2 ①
在地面附近有mg0＝GMm／R02 ②
由①②解得a＝g0R02／R2，A正确．
由GMm/R2＝mω2R＝mv2／R得
ω＝
，C错．
v＝
，B正确．
卫星运行的周期为
，D正确．
【答案】 ABD
13．地球同步卫星距地面高度为h，地球表面的重力加速度为g，地球半径为R，地球自转的角速度为ω，那么同步卫星绕地球转动的线速度为（ ）
A．v＝（R+h）ω
B．v＝
C．v＝R
D．v＝
【解析】 由v＝ω r得，同步卫星的线速度为v＝ω（R+h），A选项正确．
根据地球对卫星的引力提供卫星的向心力得G
＝mω2r
求得v＝
r＝
由mg＝G 得GM＝gR2
则v＝
C选项正确．r＝
由v＝ωr得v＝ω
D选项正确．
【答案】 ACD
14．发射同步卫星时，先将卫星发射到近地圆轨道1，然后经点火使其沿椭圆轨道2运动，最后再次点火，将卫星送入同步圆轨道3，轨道1、2相切于Q点，轨道2、3相切于P点，如图6—5—5所示，当卫星分别在1、2、3轨道上正常运动时，以下说法正确的是（ ）
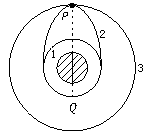
图6—5—5
A．卫星在轨道2上由Q向P运动的过程中速率越来越小
B．卫星在轨道3上经过P点的速率大于在轨道2上经过P点的速率
C．卫星在轨道2上经过Q点的半径小于在轨道2上经过P点的半径
D．卫星在轨道2上运动的周期小于在轨道3上运动的周期
【解析】 卫星在三个轨道上运动，其中在1、3轨道上做匀速圆周运动，而在2轨道上做变速率运动，且由Q到P万有引力做负功，速率减小;反之由P到Q，速率增大，故A正确．
卫星在轨道2上经过P点后，它做向心运动，而卫星在轨道3上经过P点后，仍做匀速圆周运动，由此判断B正确;由椭圆轨道的对称性可知在Q点和P点轨道半径是相等的，故C错;由开普勒第三定律可推出D选项正确．
【答案】 ABD
15．宇航员站在一星球表面上的某高处，沿水平方向抛出一小球，经过时间t，小球落到星球表面，测得抛出点与落点之间的距离L．若抛出时的初速度增大到2倍，则抛出点与落点之间的距离为L．已知两落地点在同一水平面上，该星球的半径为R，万有引力常数为G．求该星球的第一宇宙速度．
【解析】 作两次平抛的示意图如图，h为抛出点高度，x1为第一次平抛的水平距离，x2为第2次平抛的水平距离．则有:
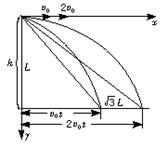
x1＝v0t ①
x2＝2v0t ②
所以x2＝2x1 ③
由几何图形知:x12+h2＝L2 ④
x22+h2＝（L）2 ⑤
由方程③④⑤可得 h＝
⑥
在竖直方向上由自由落体运动，设该星球表面重力加速度为g
h＝
gt2 ⑦
由⑥⑦两式得 g＝
由近地卫星的万有引力充当近地卫星的向心力和牛顿第二定律有:
F万＝mg＝
可得该星球的第一宇宙速度v＝
＝
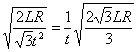
【答案】 
16．两颗卫星在同一轨道平面绕地球做匀速圆周运动，地球半径为R，a卫星离地面的高度等于R，b卫星离地面高度为3R，则
（1）a、b两卫星周期之比Ta∶Tb是多少?
（2）若某时刻两卫星正好同时通过地面同一点的正上方，则a至少经过多少个周期两卫星相距最远?
【解析】 （1）由卫星运动规律知:Ta∶Tb＝
∶
＝1∶2
（2）Ta＜Tb，当二者相距最远时，即a比b多转半圈，即
＝0．5
t＝
0．77Ta
【答案】 （1）1∶2
（2）0．77